✍[LeetCode]Dp376 摆动序列

传送门：https://leetcode-cn.com/problems/wiggle-subsequence/

题目

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。
例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值(6,-3,5,-7,3)是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5]不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

解题思路：动态规划 ［ 不够优秀 ］

🚩参考思路：https://www.yuque.com/qingxuan-u4juc/leetcode/ooel13

注意：

  - **dp[i] 含义表示以 arr[i] 结尾的最长摆动序列长度**
  - **前大后小，用dp[i][0]存储；前小后大，用dp[i][1]存储**

本题使用动态规划的方法计算最长摆动序列的长度。
记 为以 结尾，且 > 的「 最长摆动序列 」的最大长度 ；
为以 结尾，且 < 的「 最长摆动序列 」的最大长度。
只有自身自己，长度为1
显然，以下标 结尾的「 湍流子数组 」的最大长度为 ，因此边界情况为

当 时，考虑 和 之间的大小关系： 其中 的范围为：


【状态转移方程】
说明i-1是刚开始的第一个数

1. 如果 ，则如果以下标 结尾的子数组是「最长摆动序列」，应满足

1. 如果 ，则如果以下标 结尾的子数组是「最长摆动序列」，应满足

   

2. 如果 ，则 和 不能同时出现在同一个湍流子数组中，因此

   

复杂度分析

时间复杂度：，其中 为数组 的长度。

空间复杂度：，只需要维护长度为 的 数组空间。

代码

我的代码

public class Demo {
    public static int wiggleMaxLength(int[] nums) {
        // 【 1 < 2 > 3 】  、 【 1 > 2 < 3 】
        // dp[i][0] 代表dp[i-1]>【 dp[i] 】所构成最大长度
        // dp[i][1] 代表dp[i-1]<【 dp[i] 】所构成最大长度
        if(nums==null||nums.length==0)return 0;
        int [][]dp=new int[nums.length][2];
        dp[0][0]=dp[0][1]=1;
        int res=0;
        for (int i = 0; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                if(nums[i]>nums[j]){
                    dp[i][1]=Math.max(dp[i][1],dp[j][0]+1);
                    dp[i][0]=Math.max(1,dp[i][0]);
                }else if(nums[i]<nums[j]){
                    dp[i][0]=Math.max(dp[i][0],dp[j][1]+1);
                    dp[i][1]=Math.max(1,dp[i][1]);
                }else{//二者等于,废了
                    dp[i][1]=Math.max(1,dp[i][1]);
                    dp[i][0]=Math.max(1,dp[i][0]);
                }
            }
            res=Math.max(res,Math.max(dp[i][0],dp[i][1]));
        }
        return res;
    }

    public static void main(String[] args) {
        System.out.println(wiggleMaxLength(new int[]{1,17,5,10,13,15,10,5,16,8}));
    }
}

前言

解决本题前，我们先进行一些约定：

1. 某个序列被称为「上升摆动序列」，当且仅当该序列是摆动序列，且最后一个元素呈上升趋势。如序列 [1,3,2,4][1,3,2,4] 即为「上升摆动序列」。

2. 某个序列被称为「下降摆动序列」，当且仅当该序列是摆动序列，且最后一个元素呈下降趋势。如序列 [4,2,3,1][4,2,3,1] 即为「下降摆动序列」。

3. 特别地，对于长度为 1 的序列，它既是「上升摆动序列」，也是「下降摆动序列」。

4. 序列中的某个元素被称为「峰」，当且仅当该元素两侧的相邻元素均小于它。如 [1,3,2,4][1,3,2,4中， 3 就是一个「峰」。

5. 序列中的某个元素被称为「谷」，当且仅当该元素两侧的相邻元素均大于它。如 [1,3,2,4][1,3,2,4中， 2 就是一个「谷」。

6. 特别地，对于位于序列两端的元素，只有一侧的相邻元素小于或大于它，我们也称其为「峰」或「谷」。如序列 [1,3,2,4][1,3,2,4] 中，1 既是一个「谷」，4 也是一个「峰」。

7. 因为一段相邻的相同元素中我们最多只能选择其中的一个，所以我们可以忽略相邻的相同元素。现在我们假定序列中任意两个相邻元素都不相同，即要么左侧大于右侧，要么右侧大于左侧。对于序列中既非「峰」也非「谷」的元素，我们称其为「过渡元素」。如序列 [1,2,3,4][1,2,3,4] 中，2 和 3 都是「过渡元素」。

解题思路：动态规划

并非一定要nums[ i ]结尾

1. 表示以前 个元素中的某一个为结尾的最长的「上升摆动序列」的长度。

2. 表示以前 个元素中的某一个为结尾的最长的「下降摆动序列」的长度。

下面以 为例，说明其状态转移规则：

1. 当 时，对于任何以 结尾的，都可将其替换为

使其成为以 结尾的「上升摆动序列」。

1. 当 时，需要考虑两种情形，具体谁的值更大 。
   • 一、使用 的长度 [ **nums[i]** 与 **nums[i-1]** 冲突 ]
   • 二、 使用 的长度

解释：关于 **Down[i-1]** 的合法性证明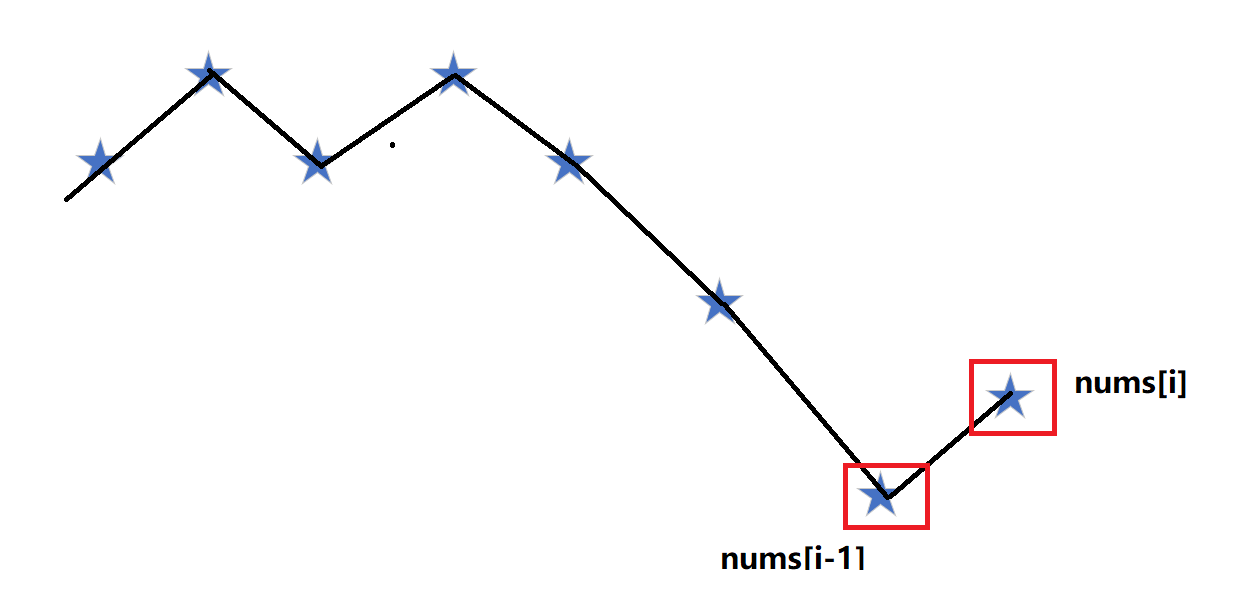

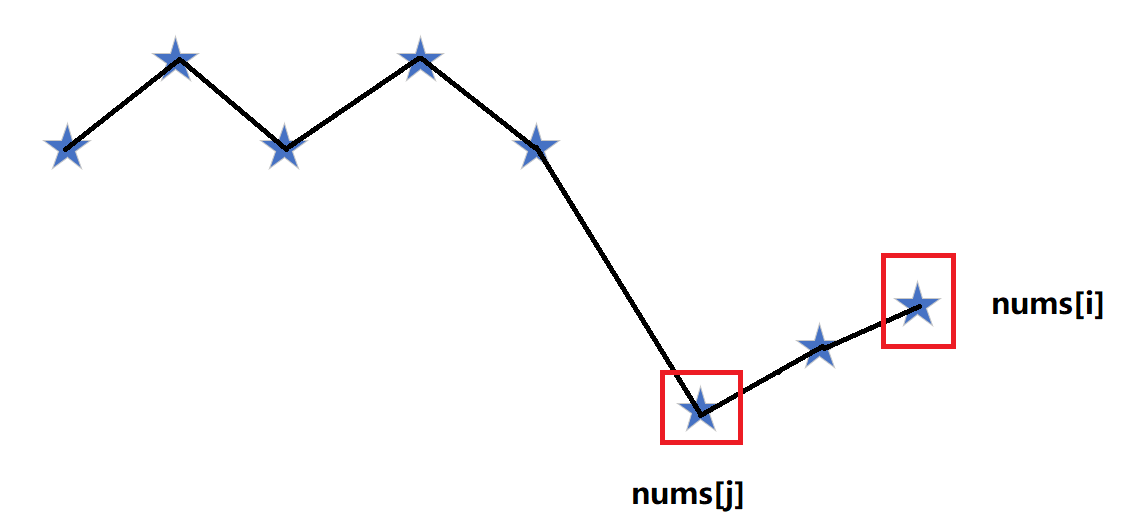
状态转移方程：

最终的答案即为 和 中的较大值，其中 是序列的长度。

复杂度分析

时间复杂度：，其中 为数组 的长度。

空间复杂度：，只需要维护2个长度为 的 数组空间。

代码

官方代码

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int n = nums.length;
        if (n < 2) {
            return n;
        }
        int[] up = new int[n];
        int[] down = new int[n];
        up[0] = down[0] = 1;
        for (int i = 1; i < n; i++) {
            if (nums[i] > nums[i - 1]) {
                up[i] = Math.max(up[i - 1], down[i - 1] + 1);
                down[i] = down[i - 1];
            } else if (nums[i] < nums[i - 1]) {
                up[i] = up[i - 1];
                down[i] = Math.max(up[i - 1] + 1, down[i - 1]);
            } else {
                up[i] = up[i - 1];
                down[i] = down[i - 1];
            }
        }
        return Math.max(up[n - 1], down[n - 1]);
    }
}

滚动数组优化：

后面的变量只和前面的两个变量有关，因此只用维护两个变量

复杂度分析

时间复杂度：，其中 为数组 的长度。

空间复杂度：，只需要维护 2 个变量，需要常数空间。

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int n = nums.length;
        if (n < 2) {
            return n;
        }
        int up = 1, down = 1;
        for (int i = 1; i < n; i++) {
            if (nums[i] > nums[i - 1]) {
                up = Math.max(up, down + 1);
            } else if (nums[i] < nums[i - 1]) {
                down = Math.max(up + 1, down);
            }
        }
        return Math.max(up, down);
    }
}