[LC]406. 根据身高重建队列

🚩传送门：力扣题目

题目

假设有打乱顺序的一群人站成一个队列，数组 表示队列中一些人的属性（不一定按顺序）。

每个 表示第 个人的身高为 ，前面正好有 个身高大于或等于 的人。

请你重新构造并返回输入数组 所表示的队列。返回的队列应该格式化为数组 ，其中 是队列中第 个人的属性 。
（ 是排在队列前面的人）

示例 1：

输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]] 输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 解释： 编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。 编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。 编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。 编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。 编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。 编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。 因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。

解题思路：排序

一般这种数对，还涉及排序的，根据第一个元素正向排序，根据第二个元素反向排序，或者根据第一个元素反向排序，根据第二个元素正向排序，往往能够简化解题过程。

在本题目中，我首先对数对进行排序，按照数对的元素 1 降序排序，按照数对的元素 2 升序排序，我们希望元素 2 大的尽量在后面，不止是为了减少插入次数，也是为了保证正确性。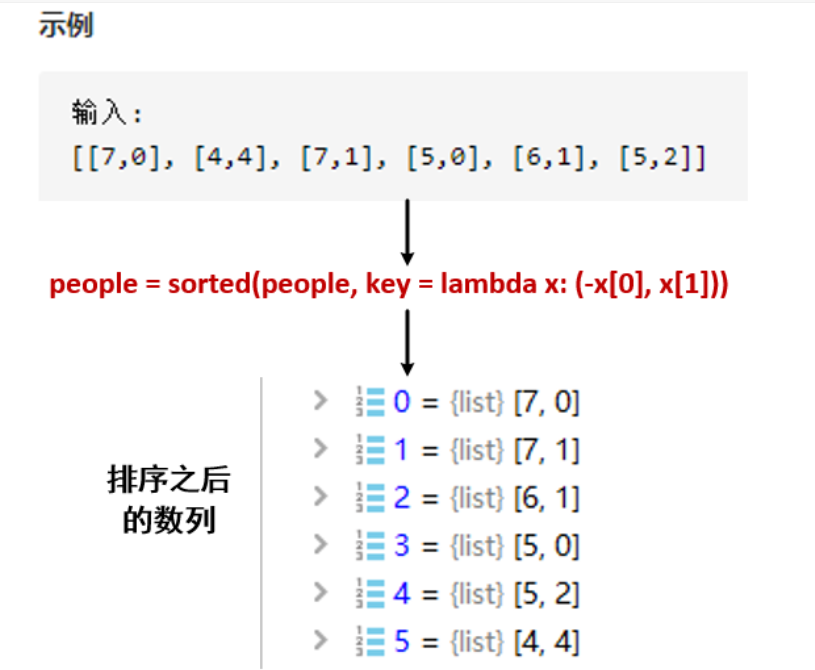







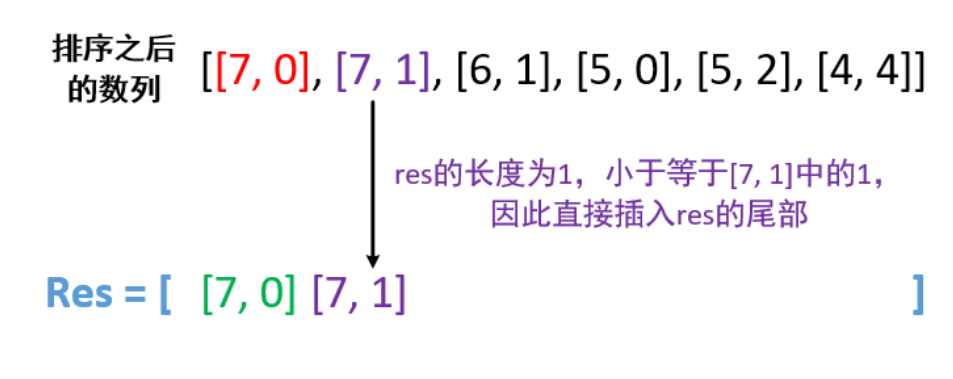
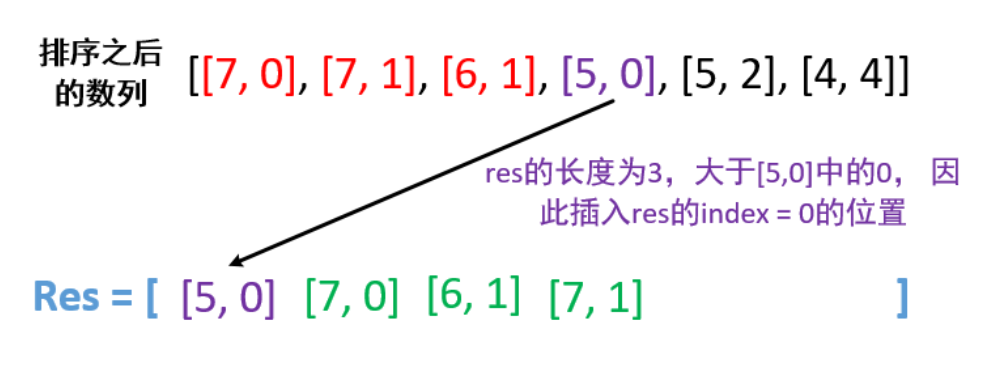
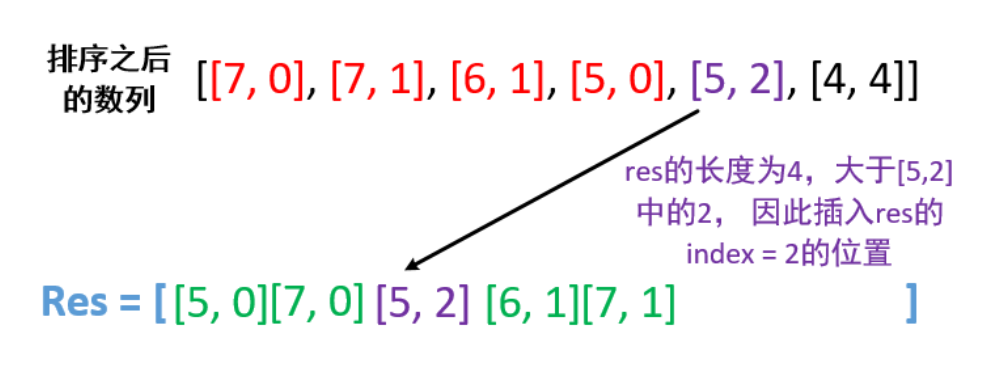
我们不难发现，元素 2 就是在 数组中的下标

复杂度分析

时间复杂度： ，其中 是 的长度，排序所需要的时间复杂度。

空间复杂度：

官方代码

class Solution {
    public int[][] reconstructQueue(int[][] people) {
        // 0 元素降序、1元素升序
        Arrays.sort(people, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[0]==o2[0]?o1[1]-o2[1]:o2[0]-o1[0];
            }
        });
        ArrayList<int[]>list=new ArrayList<>();
        // 按照元素2的下标插入
        for (int i = 0; i < people.length; i++) {
            list.add(people[i][1],people[i]);
        }
        return list.toArray(new int[list.size()][]);
    }
}