🚩传送门：牛客题目

题目

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

由于nums[n] = -∞因此最后一个数只需要大于旁边的即可

示例 1：

输入：nums = [1,2,3,1] 输出：2 解释：3 是峰值元素，你的函数应该返回其索引 2。

示例 2：

输入：nums = [1,2,1,3,5,6,4] 输出：1 或 5 解释：你的函数可以返回索引 1，其峰值元素为 2；或者返回索引 5， 其峰值元素为 6。

解题思路：迭代爬坡

如果我们从一个位置开始，不断地向高处走，那么最终一定可以到达一个峰值位置。原因如下：

  • 有下折：要么数组数值有变小，成立
  • 要么数组一直单调递增，但是由于_nums[n] = -∞ _，故也成立

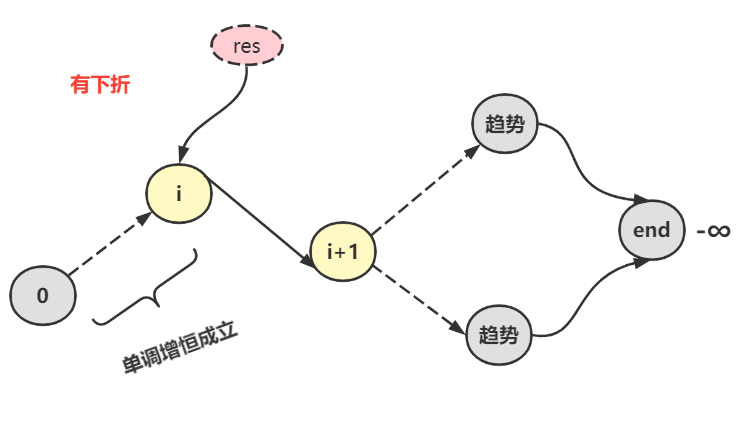
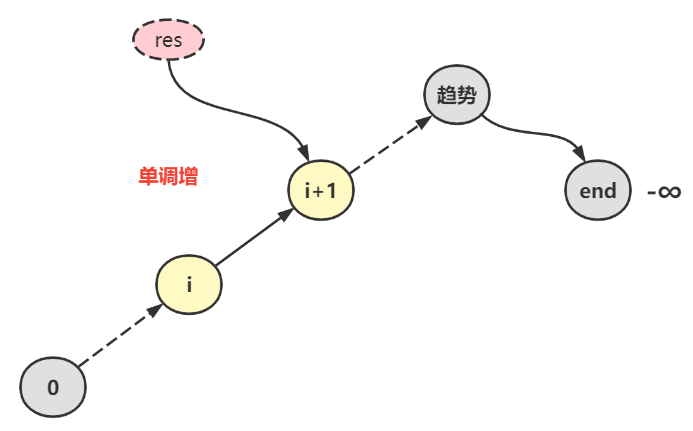
image.pngimage.png

因为只要出现nums[i] > nums[i+1]时，当前的i处就是山峰。

i = 0时，-_∞ _= nums[-1] < nums[0] > nums[1] 必然成立 …. …. …. 爬坡 …. …. …. 单调增 …. …. …. nums[i] < nums[i+1] 恒成立 i = X时，nums[X] > nums[X+1]必然成立

i = end时，nums[i-1] < nums[i] > nums[n] = -_∞_ 必然成立


复杂度分析

时间复杂度： BM[19]. 寻找峰值 - 图3 ，其中 BM[19]. 寻找峰值 - 图4 是数组 BM[19]. 寻找峰值 - 图5 的长度。在最坏情况下，数组BM[19]. 寻找峰值 - 图6 单调递增，这样就需要向右走到数组的最后一个位置。

空间复杂度：BM[19]. 寻找峰值 - 图7

我的代码

  1. // 找出第一个出现的山峰下标
  2. public int findPeakElement(int[] nums) {
  3.     int idx = 0;
  4.     for (int i = 1; i < nums.length; ++i) {
  5.         // 当当前数大于右侧数,说明此时是山峰
  6.         if (nums[idx] > nums[i]) break;
  7.         idx = i;
  8.     }
  9.     return idx;
  10. }
  12. // 找出最后一个出现的山峰下标
  13. public int findPeakElement(int[] nums) {
  14.     int idx = 0;
  15.     for (int i = 1; i < nums.length; ++i) {
  16.         // 保持向右的递增趋势
  17.         if (nums[idx] < nums[i]) {
  18.             idx = i;
  19.         }
  20.     }
  21.     return idx;
  22. }

解题思路：二分爬坡查找

  • 当 _nums[mid] < nums[mid+1]_时，_left =mid+1_保持上升爬坡趋势
  • 当 _nums[mid] > nums[mid+1]_时，_right=mid+1_保持上升爬坡趋势

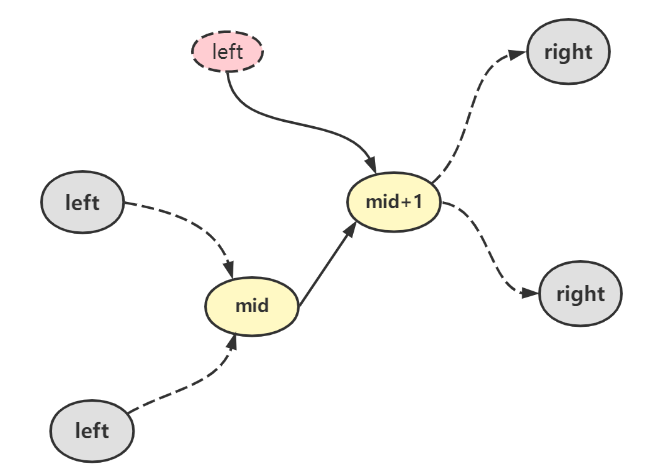
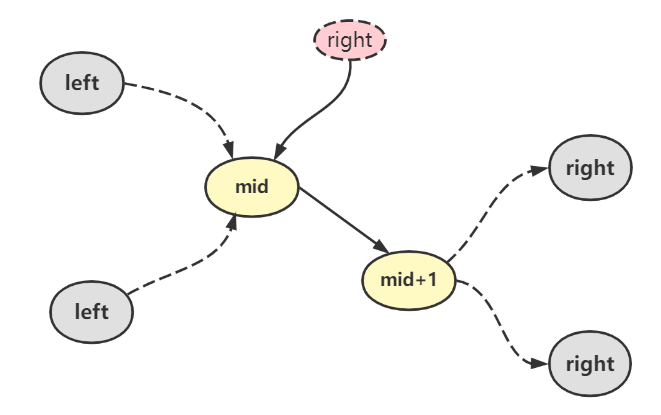
image.pngimage.png
如图所示，最后二分查找下标left和right快要相等时，一定是此等情况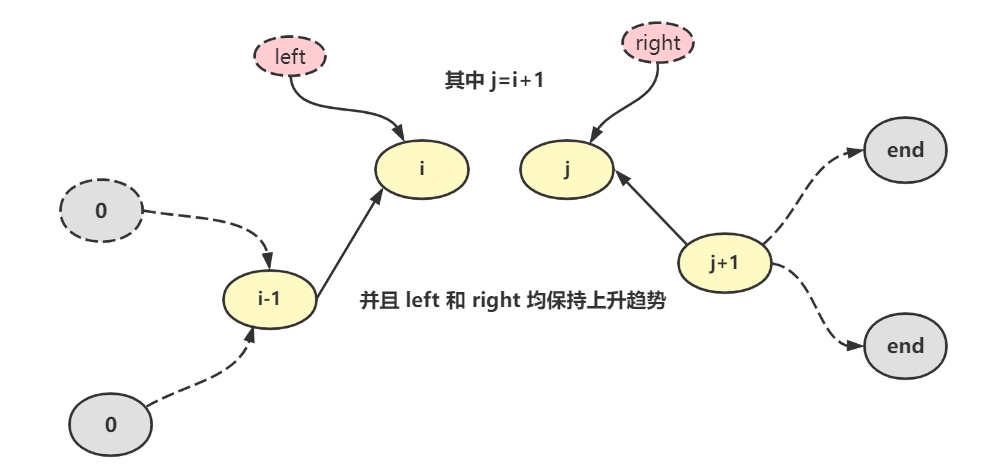
image.png
我们知道对于二分查找的逼近，最终一定会来到 left = right，当 left 和 right 经过判断后一定会有下列的情况出现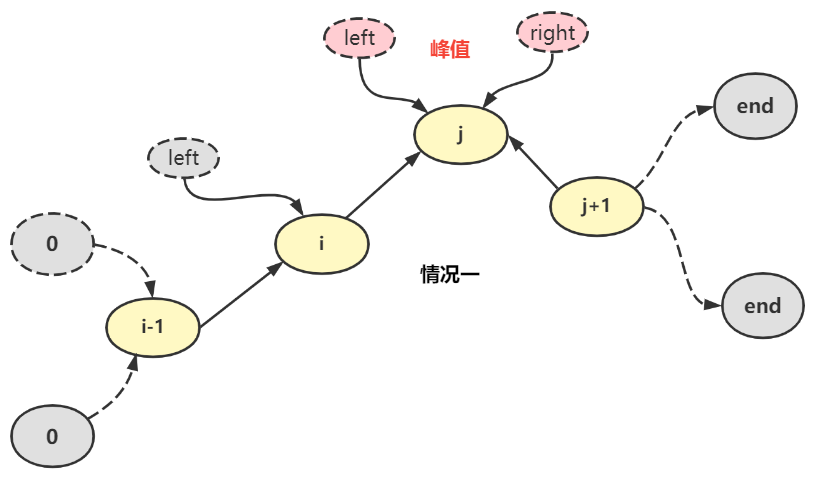
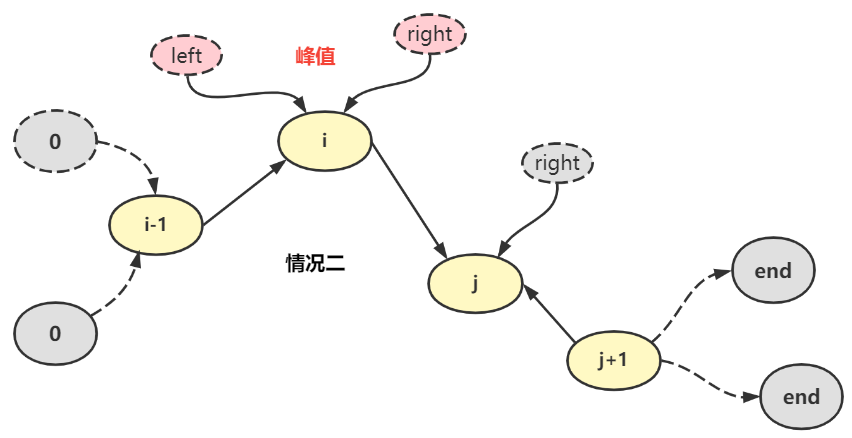
image.pngimage.png

复杂度分析

时间复杂度： BM[19]. 寻找峰值 - 图13 ，其中 BM[19]. 寻找峰值 - 图14 是数组 BM[19]. 寻找峰值 - 图15 的长度。

空间复杂度：BM[19]. 寻找峰值 - 图16

我的代码

  1. public class Solution {
  3.     public int findPeakElement (int[] nums) {
  4.         //关键思想：下坡的时候可能找到波峰，也可能找不到。但只要不断上坡一定能找到波峰 , 因为 nums[n] = -∞
  5.         int left = 0;
  6.         int right = nums.length-1;
  7.         while(left < right){
  8.             int mid = left+(right-left)/2;            // 防止溢出
  9.             if(nums[mid]<nums[mid+1]) left=mid+1;    // 这里是右边的路是上坡路,left 上坡
  10.             else right = mid;                        // 这里是左边的路是上坡路,right上坡
  11.         }
  12.         return left;
  13.     }
  14. }