[LeetCode]Dp375 猜数字大小 II

传送门：https://leetcode-cn.com/problems/guess-number-higher-or-lower-ii/

题目

我们正在玩一个猜数游戏，游戏规则如下：

我从 1 到 n 之间选择一个数字，你来猜我选了哪个数字。每次你猜错了，我都会告诉你，猜大了或者小了。然而，当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。直到你猜中我选的数字，你才算赢了这个游戏。

示例：

n = 10, 我选择了8.

第一轮: 你猜我选择的数字是5，我会告诉你，我的数字更大一些，然后你需要支付5块。 第二轮: 你猜是7，我告诉你，我的数字更大一些，你支付7块。 第三轮: 你猜是9，我告诉你，我的数字更小一些，你支付9块。

游戏结束。8 就是我选的数字。

你最终要支付 5 + 7 + 9 = 21 块钱。

给定 n ≥ 1，计算你至少需要拥有多少现金才能确保你能赢得这个游戏。

解题思路：动态规划

首先声明，二分法是错的，二分能在最少的次数内猜中，却无法保证在最少的花费下赢得游戏 。

二分只能把中间的数字当作分割点，而动态规划可以穷举所有的情况 。

动态规划：1 2 3 4 5 在第一次猜数时，我们可以猜1，2，3，4，5 二分查找：1 2 3 4 5 在第一次猜数时，我们只能猜 3

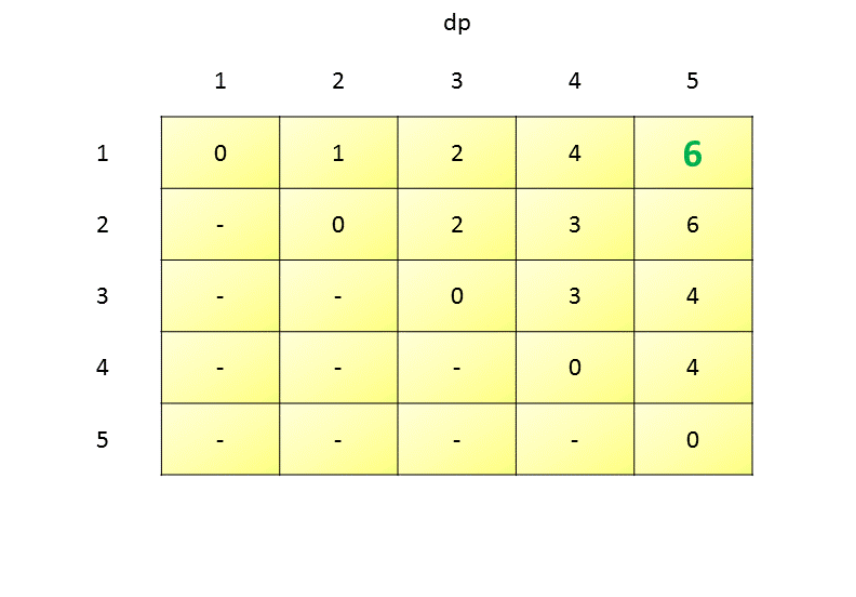
表示从 到 依次作为分割点(猜的数)，所能赢的游戏所用钱的最小值 。似乎很难理解 。

1. 解释dp[1][1]

dp[1][1]=0，因为只有一个数字1 。我们只能猜1，答案也只能是1，不用花钱 。

1. 解释dp[1][2]

dp[1][2]是指只有两个数字1，2 。

1 做分割点

猜1： 答案是1，花费0元 答案是2，花费1元 必定赢得游戏，最多花费1元

2 做分割点

猜2： 答案是1，花费2元 答案是2，花费0元 必定赢得游戏，最多花费2元

综上，只要进入 这个区间，我们第一次猜 1，只要花费 1 元，必定可以赢得游戏

1. 解释dp[2][3]

dp[2][3]是指只有两个数字2，3

有一个小问题，为什么不是从1开始呢 ？

设 n=3，第一次猜了1，但是答案是2或者3，反正不是1，我们要到[2,3]区间来寻找答案，即求dp[2][3]

2 做分割点

猜2： 答案是2，花费0元 答案是3，花费2元 必定赢得游戏，最多花费2元

3 做分割点

猜3： 答案是2，花费3元 答案是3，花费0元 必定赢得游戏，最多花费3元

综上，只要进入 这个区间，我们第一次猜2，只要花费2元，必定可以赢得游戏 。

1. 解释dp[1][3]

dp[1][3]是指只有三个数字1，2，3

1 做分割点

猜1： 答案是1，花费0元 答案是2或者3，这个时候会进入另一个区间[2,3]，花费1+dp[2][3]元必定赢得游戏

最多花费 **max(0,1+dp[2][3])** 元

2 做分割点

猜2： 答案是1，花费2+dp[1][1]=2+0=2元 答案是2，花费0元 答案是3，花费2+dp[3][3]=2+0=2元

最多花费 **max(0,2+dp[1][1],2+dp[3][3])** 元

3 做分割点

猜3： 答案是1或者2,花费3+dp[1][2]元 答案是3，花费0元 必定赢得游戏
最多花费 **max(0,3+dp[1][2])** 元

综上，只要进入 这个区间，我们只要花费 min( max(0,1+dp[2][3]) , max(0,2+dp[1][1],2+dp[3][3]) , max(0,3+dp[1][2]) )元必定可以赢的游戏而dp[1][3]也就等于那个min的值。

可以发现，只要找到dp[1][n]即可符合题目的意思。

状态转移方程：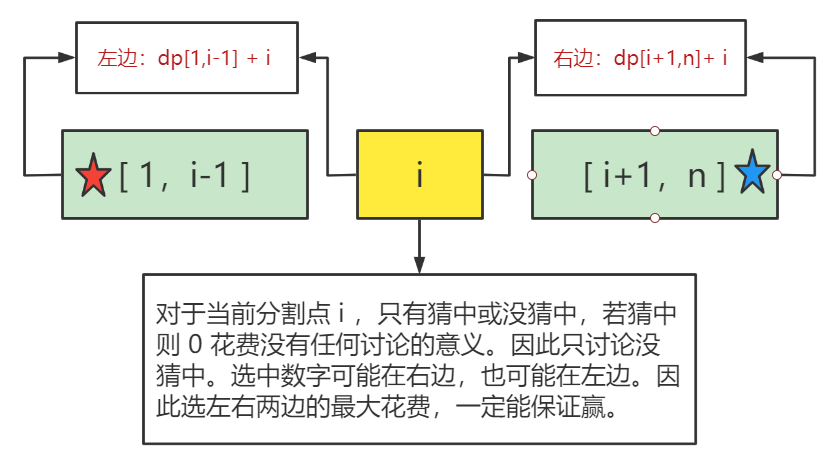
非区间端点：
对于每一个分割点，我们取它左右两边区间的最大值加上分割点的值作为取此分割点的dp[i][j]值，对于每一个区间，我们取所有分割点的dp[i][j]的最小值作为dp[i][j]的真正的值
区间端点：

1. 对于以i作为分割点的dp[i][j]，只取i右边的区间
2. 对于以j作为分割点的dp[i][j]，只取j左边的区间

i，i+1，… ，X-1，X，X+1 ，… ，j-1，j

以i为分割点：dp0=i+dp[i+1][j] 以j为分割点：dp1=j+dp[i][j-1] 以X为分割点：dp2=max(dp[i][X-1],dp[x+1][j])+X (其中 i<X<j)

综上：dp[i][j]=min(dp0,dp1,dp2)

代码

我的代码

class Solution {
public:
    int getMoneyAmount(int n) {
        if(n==1)return 0;
        //定义矩阵
        int dp[n+1][n+1];
        //初始化\,"\"表示正无穷
        for(int i=0;i<=n;i++){
            for(int j=0;j<=n;j++){
                dp[i][j]=INT_MAX;
            }
        }
        //定义基础值dp[i][i]
        for(int i=0;i<=n;i++){
            dp[i][i]=0;
        }
        //按列来，从第2列开始                            [ 区间的右端点 ]
        for(int j=2;j<=n;j++){
            //按行来，从下往上                             [ 区间的左端点 ]
            for(int i=j-1;i>=1;i--){
                //算除了两端的每一个分割点                   [ 区间的分割点 ]
                for(int X=i+1;X<=j-1;X++){
                    dp[i][j]=min(X+max(dp[i][X-1],dp[X+1][j]),dp[i][j]);
                }
                //算两端
                dp[i][j]=min(dp[i][j],i+dp[i+1][j]);    [ 区间端点i ]
                dp[i][j]=min(dp[i][j],j+dp[i][j-1]);    [ 区间端点j ]
            }
        }
        return dp[1][n];
    }
};