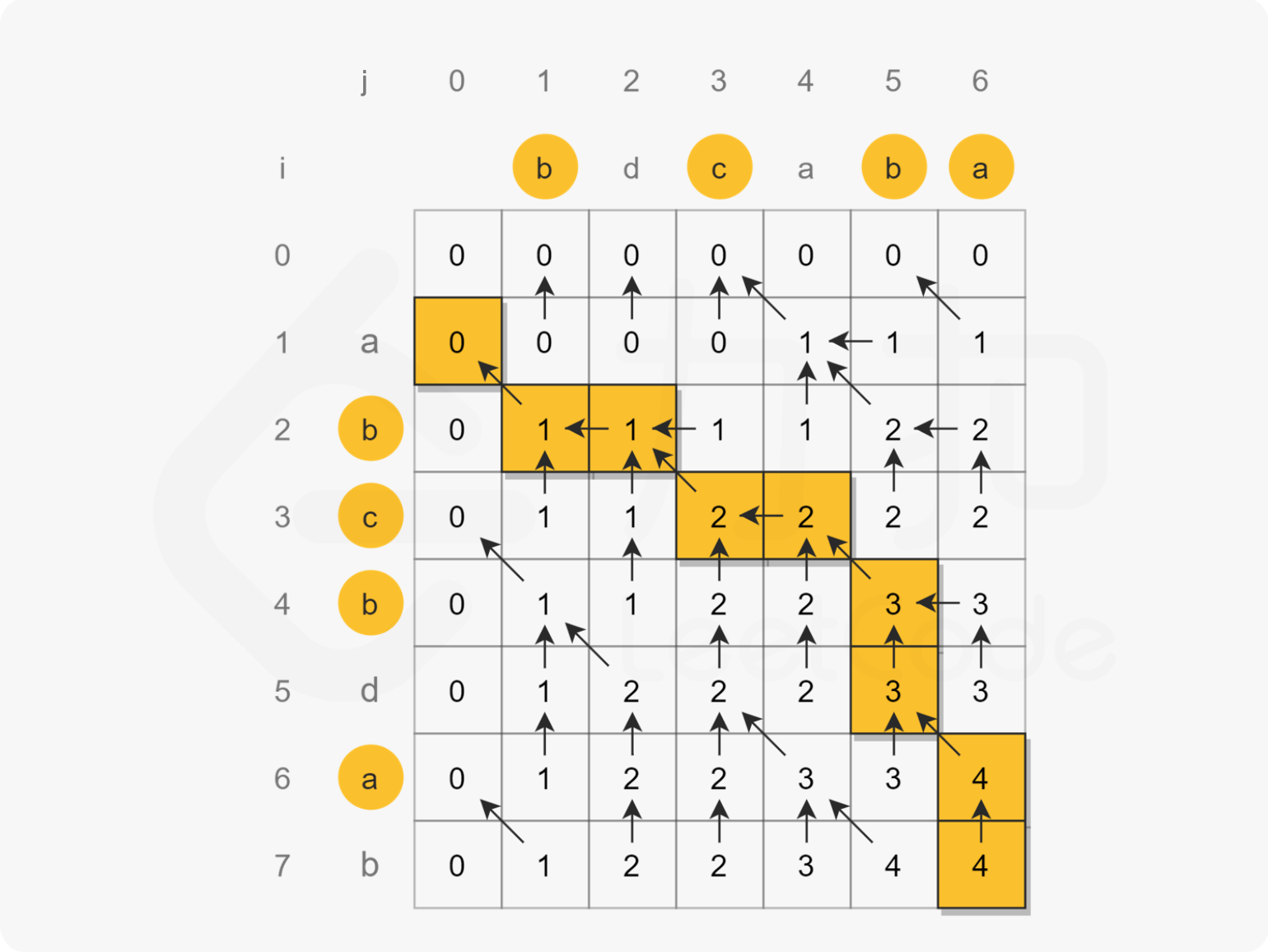
基本概念
科普下,最长公共子序列()和最长公共子串(
)不是一回事儿。
什么是子序列、子串呢?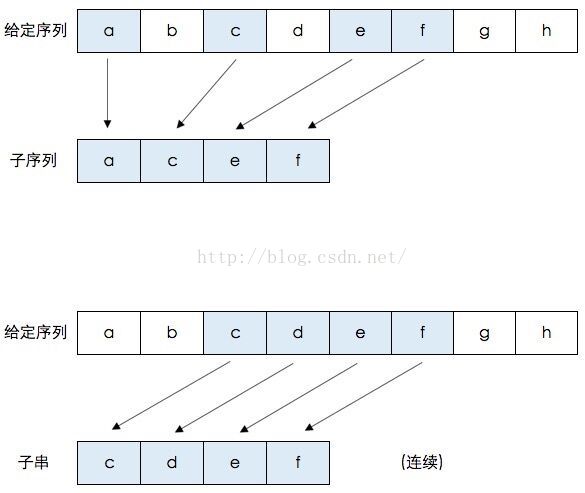
最长公共子序列(以下都简称 LCS )
解题子序列问题:动态规划
求解LCS问题,不能使用暴力搜索方法。一个长度为 的序列拥有
次方个子序列,它的时间复杂度是指数阶,太恐怖了。解决LCS问题,需要借助动态规划的思想。
假设字符串 和
的长度分别为
和
,创建
行
列的二维数组
👉 定义 表示为
和
的最长公共子序列的长度。
上述表示中
text1[0:i]表示 text1 的长度为 i 的前缀,text2[0:j]表示 text2 的长度为 j 的前缀。
考虑动态规划的边界情况:
- 当
时,
为空,空字符串和任何字符串的最长公共子序列的长度都是
,因此对任意
,有
;
- 当
时,
为空,空字符串和任何字符串的最长公共子序列的长度都是
,因此对任意
,有
;
因此动态规划的边界情况是:当 或
时,
。
当 且
时,考虑
的计算:
- 当
时,
。
- 考虑
和
的最长公共子序列,再增加一个字符(即公共字符)即可得到
和
的最长公共子序列
- 当
时,考虑以下两项:
和
的最长公共子序列
和
的最长公共子序列。
和
的最长公共子序列,取两项中较大
由此可以得到状态转移方程:
复杂度分析
时间复杂度:,其中
和
分别是字符串
和
- 二维数组  有 行和列,需要对  中的每个元素进行计算。
空间复杂度:,其中
和
分别是字符串
和
- 创建了 行和列的二维数组 
我的代码 [求解长度]
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
//1. 记录 m,n 长度
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
char c1 = text1.charAt(i - 1);
for (int j = 1; j <= n; j++) {
char c2 = text2.charAt(j - 1);
//2. 如果相等
if (c1 == c2) {
//在原来的基础上长度加1
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
//3. 不相等的话需要找到最大值
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
}
我的代码 [求解序列]
class Solution {
public static String longestCommonSubsequence(String text1, String text2) {
//1. 记录 m,n 长度
int m = text1.length(), n = text2.length();
String[][] dp = new String[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
char c1 = text1.charAt(i - 1);
for (int j = 1; j <= n; j++) {
char c2 = text2.charAt(j - 1);
//2. 如果相等
if (c1 == c2) {
//在原来的基础上长度加1
dp[i][j] = dp[i - 1][j - 1]==null? c1+"":dp[i - 1][j - 1]+c1;
} else {
//3. 不相等的话需要找到最大值
dp[i][j] = ((dp[i - 1][j]==null?0:dp[i - 1][j].length()) >
(dp[i][j - 1]==null?0:dp[i][j - 1].length()))?
dp[i - 1][j]:dp[i][j - 1];
}
}
}
return dp[m][n];
}
public static void main(String[] args) {
System.out.println(longestCommonSubsequence("abcde","ace"));//ace
}
}
解题子串问题:动态规划
假设字符串 和
的长度分别为
和
,创建
行
列的二维数组
👉 定义 表示为
和
的最长公共子串的长度。
上述表示中
text1[0:i]表示 text1 的长度为 i 的前缀,text2[0:j]表示 text2 的长度为 j 的前缀。
考虑动态规划的边界情况:
- 当
时,
为空,空字符串和任何字符串的最长公共子串的长度都是
,因此对任意
,有
;
- 当
时,
为空,空字符串和任何字符串的最长公共子串的长度都是
,因此对任意
,有
;
因此动态规划的边界情况是:当 或
时,
。
当 且
时,考虑
的计算:
- 当
时,
。
- 考虑
和
的最长公共子串,再增加一个字符(即公共字符)即可得到
和
的最长公共子串
- 考虑
- 当
时,
。
由此可以得到状态转移方程:
最终计算得到 即为
和
的最长公共子串的长度。
复杂度分析
时间复杂度:,其中
和
分别是字符串
和
- 二维数组  有 行和列,需要对  中的每个元素进行计算。
空间复杂度:,其中
和
分别是字符串
和
- 创建了 行和列的二维数组 
我的代码 [求解长度]
class Solution {
public int longestCommonSubstring(String text1, String text2) {
//1. 记录 m,n 长度
int m = text1.length(), n = text2.length();
int res=0;
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
char c1 = text1.charAt(i - 1);
for (int j = 1; j <= n; j++) {
char c2 = text2.charAt(j - 1);
//2. 如果相等
if (c1 == c2) {
//在原来的基础上长度加1
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
//3. 不相等的话需要找到最大值
dp[i][j] = 0;
}
res=Math.max(res,dp[i][j]);
}
}
return res;
}
}
我的代码 [求解序列]
class Solution {
public static String longestCommonSubstring(String text1, String text2) {
//1. 记录 m,n 长度
int m = text1.length(), n = text2.length();
String res="";
String[][] dp = new String[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
char c1 = text1.charAt(i - 1);
for (int j = 1; j <= n; j++) {
char c2 = text2.charAt(j - 1);
//2. 如果相等
if (c1 == c2) {
//在原来的基础上长度加1
dp[i][j] = dp[i - 1][j - 1]==null? c1+"":dp[i - 1][j - 1]+c1;
} else {
//3. 不相等的话需要找到最大值
dp[i][j] = "";
}
res=res.length()>dp[i][j].length()?res:dp[i][j];
}
}
return res;
}
public static void main(String[] args) {
System.out.println(longestCommonSubstring("aaacbcbceef","aaabcbceed"));//bcbcee
}
}