🚩传送门:力扣题目
题目
给你一个二叉树的根节点 ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3] 输出:true 示例 2:
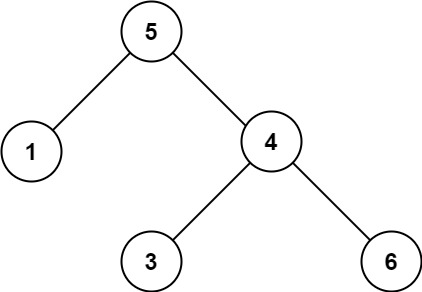
输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
解题思路:递归
- 如果该二叉树的左子树不为空,则左子树上所有节点的值均小于它的根节点的值
- 如果该二叉树的右子树不为空,则右子树上所有节点的值均大于它的根节点的值
- 它的左右子树也为二叉搜索树。
设计一个递归函数 来递归判断,表示以
为根的子树,判断子树中所有节点的值是否都在
的范围内(注意是开区间)。如果
节点的值
不在
的范围内说明不满足条件直接返回,否则我们要继续递归调用检查它的左右子树是否满足,如果都满足才说明这是一棵二叉搜索树。
在递归调用左子树时,需要把上界
改为
,即调用
因为左子树里所有节点的值均小于它的根节点的值。
同理递归调用右子树时,我们需要把下界
改为
,即调用
。
函数递归调用的入口为 ,
表示一个无穷大的值。
复杂度分析
时间复杂度:,为二叉树的节点个数。
- 二叉树的每个节点最多被访问一次,因此时间复杂度为 
空间复杂度:,为二叉树的节点个数。
- 递归函数在递归过程中需要为每一层递归函数分配栈空间,所以这里需要额外的空间且该空间取决于递归的深度,即二叉树的高度。最坏情况下二叉树为一条链,树的高度为 nn ,递归最深达到 nn 层,故最坏情况下空间复杂度为 O(n)O(n) 。
我的代码
class Solution {public boolean isValidBST(TreeNode root) {return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);}public boolean isValidBST(TreeNode node, long lower, long upper) {if (node == null)return true;if (node.val <= lower || node.val >= upper)return false;return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);}}
解题思路:中序遍历
基于二叉搜索树的性质,我们可以知道二叉搜索树「中序遍历」得到的值构成的序列一定是升序的,只要我们能确定中序遍历的序列是升序的就可以说明,整棵树是二叉搜索树。
我们在中序遍历的时候实时检查当前节点的值是否大于前一个中序遍历到的节点的值即可。如果均大于说明这个序列是升序的,整棵树是二叉搜索树,否则不是。

复杂度分析
时间复杂度:,为二叉树的节点个数。
- 二叉树的每个节点最多被访问一次,因此时间复杂度为 
空间复杂度:,为二叉树的节点个数。
- 栈最多存储  个节点,因此需要额外的  的空间。
我的代码
class Solution {public boolean isValidBST(TreeNode root) {Deque<TreeNode> stack = new LinkedList<TreeNode>();double inorder = -Double.MAX_VALUE;//#栈模拟递归while (!stack.isEmpty() || root != null) {while (root != null) {stack.push(root);root = root.left;}root = stack.pop();// 如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树if (root.val <= inorder) {return false;}inorder = root.val;root = root.right;}return true;}}

