[NC]34. 不同路径的数目 I

🚩传送门：牛客题目
力扣题目

题目

机器人在 大小的地图的左上角（起点），每次可以向下或向右移动。要到达地图的右下角（终点）。
可以有多少种不同的路径从起点走到终点？
要求：空间复杂度 ，时间复杂度
进阶：空间复杂度 ，时间复杂度

示例 1：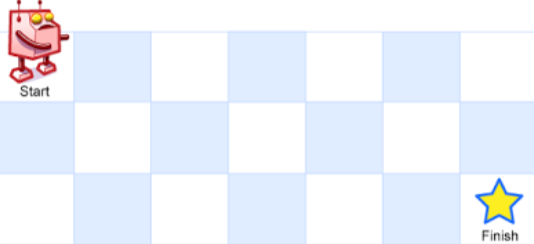

输入：m = 3, n = 7 输出：28

解题思路：动态规划

👉 定义： 表示到达坐标 的路径数量 。

我们看到这张图就明白一切：

复杂度分析

时间复杂度：，其中 为数组的行数，其中 为数组列数 。

空间复杂度：，其中 为数组的行数，其中 为数组列数 。

官方代码

public int uniquePaths (int m, int n) {
        // 定义dp数组
        int[][] dp = new int[m][n];
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                // 当 i = 0：dp[0][j] = dp[0][j-1]
                if(i == 0){
                    dp[i][j] = 1; // 都是1是因为dp[0][j] = dp[0][j-1]，所以干脆全部赋值为1
                    continue;
                }
                // 当 j = 0：dp[i][0] = dp[i-1][0]
                if(j == 0){
                    dp[i][j] = 1;
                    continue;
                }
                // 当 i > 1 && j > 1 :  dp[i][j] = dp[i][j-1] + dp[i-1][j]
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1]; // 返回到达终点的所有可行路径
    }