🍗只出现一次的合集整理

解1：第一个只出现一次的字符

题目

在字符串 s 中找出第一个只出现一次的字符。如果没有，返回一个单空格。 s 只包含小写字母。

示例 1:

输入：s = “abaccdeff” 输出：‘b’

示例 2:

输入：s = “” 输出：‘ ‘

思路

我们可以对字符串进行两次遍历。
在第一次遍历时，我们使用哈希映射统计出字符串中每个字符出现的次数。在第二次遍历时，我们只要遍历到了一个只出现一次的字符，那么就返回该字符，否则在遍历结束后返回空格。

复杂度分析

时间复杂度： ，其中 是字符串 s 的长度。我们需要进行两次遍历。

空间复杂度： ，其中 是字符集，在本题中 s 只包含小写字母，因此 。需要 的空间存储哈希映射。

官方代码

class Solution {
    public char firstUniqChar(String s) {
        Map<Character, Integer> frequency = new HashMap<Character, Integer>();
        for (int i = 0; i < s.length(); ++i) {
            char ch = s.charAt(i);
            frequency.put(ch, frequency.getOrDefault(ch, 0) + 1);
        }
        for (int i = 0; i < s.length(); ++i) {
            if (frequency.get(s.charAt(i)) == 1) {
                return s.charAt(i);
            }
        }
        return ' ';
    }
}

🚩我们可以对方法一进行修改，使得第二次遍历的对象从字符串变为哈希映射。
具体地，对于哈希映射中的每一个键值对，键 key 表示一个字符，值 value 表示为：

• 如果该字符只出现一次，值 value 为它的首次出现的**索引**
• 如果该字符出现多次，值 value 为 -1

  当我们第一次遍历字符串时，设当前遍历到的字符为 c，如果 c 不在哈希映射中，我们就将 c 与它的索引作为一个键值对加入哈希映射中，否则我们将 c 在哈希映射中对应的值修改为 −1。

在第一次遍历结束后，我们只需要再遍历一次哈希映射中的所有值，找出其中不为 −1 的最小值，即为第一个不重复字符的索引，然后返回该索引对应的字符。如果哈希映射中的所有值均为 −1，我们就返回空格。

时间复杂度： ，其中 是字符串 s 的长度。需要进行两次遍历。第一次遍历时间复杂度为 ，第二次遍历哈希映射的时间复杂度为 ，将方法一从 优化到 （此处优化的地方）。

空间复杂度： ，其中 是字符集，在本题中 s 只包含小写字母，因此 。需要 的空间存储哈希映射。

官方代码 [ 推荐 ]

class Solution {
    public char firstUniqChar(String s) {
        Map<Character, Integer> position = new HashMap<Character, Integer>();
        int n = s.length();
        for (int i = 0; i < n; ++i) {
            char ch = s.charAt(i);
            if (position.containsKey(ch)) {
                position.put(ch, -1);
            } else {
                position.put(ch, i);
            }
        }
        int first = n;
        for (Map.Entry<Character, Integer> entry : position.entrySet()) {
            int pos = entry.getValue();
            if (pos != -1 && pos < first) {
                first = pos;
            }
        }
        return first == n ? ' ' : s.charAt(first);
    }
}

解2：只出现一次的数字 I

题目

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1] 输出: 1

示例 2:

输入: [4,1,2,1,2] 输出: 4

思路

🚩我的此题解题报告
如果不考虑时间复杂度和空间复杂度的限制，这道题有很多种解法，可能的解法有如下几种。

1. 使用集合存储数字。遍历数组中的每个数字，如果集合中没有该数字，则将该数字加入集合，如果集合中已经有该数字，则将该数字从集合中删除，最后剩下的数字就是只出现一次的数字。
2. 使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数，并更新哈希表，最后遍历哈希表，得到只出现一次的数字。
3. 使用集合存储数组中出现的所有数字，并计算数组中的元素之和。由于集合保证元素无重复，因此计算集合中的所有元素之和的两倍，即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次，其余元素都出现两次，因此用集合中的元素之和的两倍减去数组中的元素之和，剩下的数就是数组中只出现一次的数字。

上述三种解法都需要额外使用 的空间，其中 是数组长度。

如何才能做到线性时间复杂度和常数空间复杂度呢 ？答案是使用位运算

对于这道题，可使用异或运算 ⊕ 。异或运算有以下三个性质

1. 任何数和 0 做异或运算，结果仍然是原来的数，即 _a_⊕0=_a_。
2. 任何数和其自身做异或运算，结果是 0，即 _a_⊕_a_=0。
3. 🚩异或运算满足交换律和结合律，即a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。

假设数组中有 2m+1 个数，其中有 m 个数各出现两次，一个数出现一次。令 为出现两次的 m 个数，为出现一次的数。

根据性质 3，数组中的全部元素的异或运算结果总是可以写成如下形式：

根据性质 2 和性质 1，上式可化简和计算得到如下结果：

因此，数组中的全部元素的异或运算结果即为数组中只出现一次的数字。

复杂度分析

时间复杂度：，其中 为数组长度，只需要对数组遍历一次。

空间复杂度：

🐛最优代码

class Solution {
    public int singleNumber(int[] nums) {
        int single = 0;
        for (int num : nums) {
            single ^= num;
        }
        return single;
    }
}

解3：只出现一次的数字 II

题目

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

示例 1：

输入：nums = [2,2,3,2] 输出：3

示例 2：

输入：nums = [0,1,0,1,0,1,99] 输出：99

基础思路

我们可以使用哈希映射统计数组中每个元素的出现次数。对于哈希映射中的每个键值对，键表示一个元素，值表示其出现的次数。
在统计完成后，我们遍历哈希映射即可找出只出现一次的元素。
时间复杂度：，其中 为数组长度

空间复杂度：，哈希映射中包含最多 个元素，即需要的空间为 。

官方代码

class Solution {
    public int singleNumber(int[] nums) {
        Map<Integer, Integer> freq = new HashMap<Integer, Integer>();
        // 1. 统计频率
        for (int num : nums) {
            freq.put(num, freq.getOrDefault(num, 0) + 1);
        }
        int ans = 0;
        // 2. 计算频率为 1 的
        for (Map.Entry<Integer, Integer> entry : freq.entrySet()) {
            int num = entry.getKey(), occ = entry.getValue();
            if (occ == 1) {
                ans = num;
                break;
            }
        }
        return ans;
    }
}

思路

为了方便叙述，我们称「只出现了一次的元素」为「答案」。

数组中的元素在 （即 32 位整数）范围内，故我们可以依次计算答案的每一个二进制位是 0 还是 1。

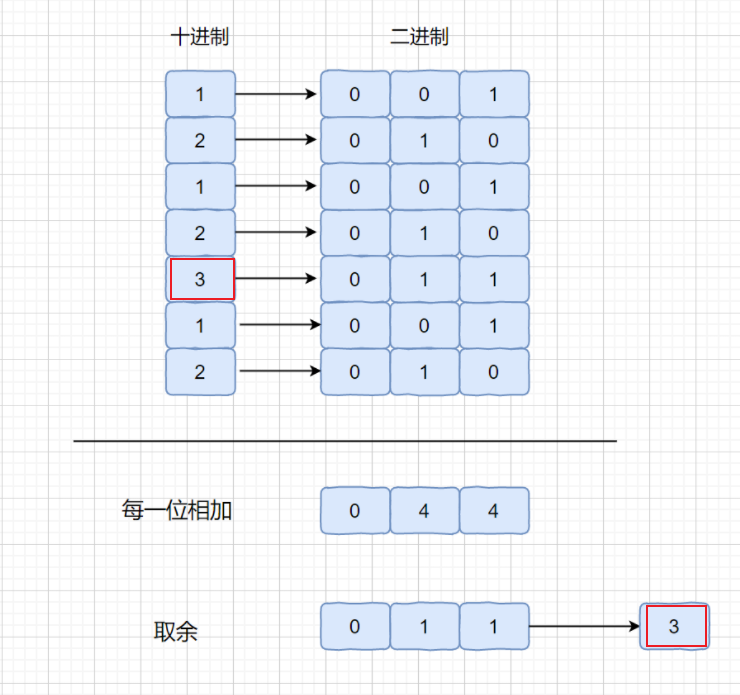
具体地，考虑答案的第 i 个二进制位（i 从 00 开始编号），它可能为 0 或 1。对于数组中非答案的元素，每一个元素都出现了 3 次，对应着第 i 个二进制位的 3 个 0 或 3 个 1，无论是哪一种情况，它们的和都是 3 的倍数（即和为 0 或 3）。因此：

🚩答案的第 i 个二进制位就是数组中所有元素的第 i 个二进制位之和除以 3 的余数

对于数组中的每一个元素 ，我们使用位运算 得到 的第 个二进制位，并将它们相加再对 3 取余，得到的结果一定为 0 或 1（不会得到2），此即为答案的第 个二进制位。

Tips：为什么不会得到 2 ，因为二进制只有 0 或者 1 ，0 加 3 次还是 0，设重复数有 m 个 1，加 3 次，值3m+独数对 3 取余 ，余数只会是 独数 。

需要注意的是，如果使用的语言对「有符号整数类型」和「无符号整数类型」没有区分，那么可能会得到错误的答案。这是因为「有符号整数类型」（即 int 类型）的第 31 个二进制位（即最高位）是补码意义下的符号位，对应着 ，而「无符号整数类型」没有符号，第 31 个二进制位对应着。

👀因此在某些语言（例如 Python）中需要对最高位进行特殊判断。

复杂度分析

时间复杂度：，其中 为数组长度， 是元素的数据范围

  - 本题中 ![](https://cdn.nlark.com/yuque/__latex/3cf3ea9596abd345c85cebc72dff9f7f.svg#card=math&code=%20%5Clog%20C%3D%5Clog%202%5E%7B32%7D%3D32&id=A4oF7)    ，也就是我们需要遍历第 `0∼31` 个二进制位。

空间复杂度：

🚩官方代码

class Solution {
    public int singleNumber(int[] nums) {
        int ans = 0;
        for (int i = 0; i < 32; ++i) {
            int total = 0;
            for (int num: nums) {
                total += ((num >> i) & 1);
            }
            if (total % 3 != 0) {
                ans |= (1 << i);
            }
        }
        return ans;
    }
}

🍗极端优化：在上述方法中，我们是依次处理每一个二进制位的，那么时间复杂度中就引入了 这一项。既然我们在对两个整数进行普通的二元运算时，都是将它们看成整体进行处理的，那么我们是否能以普通的二元运算为基础，同时处理所有的二进制位？

答案是可以的。

按照题意的要求，我们定义一种运算如果某个数出现3次，通过这种运算就让他的结果变成0，也就是说周期是3。每个数都会有下面几种状态

• 出现0次
• 出现1次
• 出现2次
• 出现3次

因为周期是3，当出现3次的时候可以认为出现了0次，也就是下面几种状态

• 出现0次
• 出现1次
• 出现2次

看到这里其实大家已经想到了，这不就是传说中的3进制吗。
在二进制中一个位置要么是1要么是0，只能表示两种状态，如果要表示3种状态我们可以使用两位数字来表示，我们选择：

• **00**表示出现**0**次
• **01**表示出现**1**次
• **10**表示出现**2**次

对于每一个数字，如果是 0 我们就不用了管他，只有是 1 的时候状态才会改变，输出是下一个状态

3 种状态

  存储    输入   结果
   ab      c     ab   （输入是1的时候，输出会变为下一个状态）
   00      1     01   （关键:如果只出现一次，结果会保存在b中，所以最后只需要返回b即可）
   01      1     10
   10      1     00

   00      0     00   （输入是0的时候，输出不变）
   01      0     01
   10      0     10

  所以可以列出下面公式
  a= ~a&b&c|a&~b&~c
  b= ~a&~b&c|~a&b&~c

代码描述

public int singleNumber(int[] nums) {
    int a = 0, b = 0;
    for (int c : nums) {
        //防止a的值被修改，在计算b的时候有影响，
        //这里在b计算完之后再对a赋值
        int tempa = ~a & b & c | a & ~b & ~c;
        b = ~a & ~b & c | ~a & b & ~c;
        a = tempa;
    }
    return b;
}

上面我们选择用00，01，01二进制表示三种状态。那么能不能选择其他状态能，当然是可以的，比如我们选择00，01，11二进制表示三种状态。

 3 种状态

  存储    输入   结果
   ab      c     ab   （输入是1的时候，输出会变为下一个状态）
   00      1     01   （关键:如果只出现一次，结果会保存在b中，所以最后只需要返回b即可）
   01      1     11
   11      1     00

   00      0     00   （输入是0的时候，输出不变）
   01      0     01
   11      0     11

  所以可以列出下面公式
  a= ~a&b&c|a&b&~c
  b= ~a&~b&c|~a&b&c|~a&b&~c|a&b&~c

代码描述

public int singleNumber(int[] nums) {
    int a = 0, b = 0;
    for (int c : nums) {
        //防止a的值被修改，在计算b的时候有影响，
        //这里在b计算完之后再对a赋值
        int tempa = ~a & b & c | a & b & ~c;
        b = ~a & ~b & c | ~a & b & c | ~a & b & ~c | a & b & ~c;
        a = tempa;
    }
    return b;
}

除了上面提到的使用两位数字，难道就不能使用三位数字吗，当然也是可以的，比如我们使用3个数字001，010，100来表示三种状态，我们来看一下：

3 种状态

  存储    输入   结果
   abc      d     abc   （输入是1的时候，输出会变为下一个状态）
   001      1     010   （关键:如果只出现一次，结果会保存在b中，所以最后只需要返回b即可）
   010      1     100
   100      1     001

   001      0     001   （输入是0的时候，输出不变）
   010      0     010
   100      0     100

  所以可以列出下面公式
  a = ~a & b & ~c & d | a & ~b & ~c & ~d
  b = ~a & ~b & c & d | ~a & b & ~c & ~d
  c = a & ~b & ~c & d | ~a & ~b & c & ~d

代码描述

public int singleNumber(int[] nums) {
    //因为默认是001，所以c的位置我们让他全部变为1
    int a = 0, b = 0, c = - 1;
    for (int d : nums) {
        int tempa = ~a & b & ~c & d | a & ~b & ~c & ~d;
        int tempb = ~a & ~b & c & d | ~a & b & ~c & ~d;
        c = a & ~b & ~c & d | ~a & ~b & c & ~d;
        a = tempa;
        b = tempb;
    }
    return b;
}

🚩公式怎么来的，其实这个很简单，就拿我下面写的状态机来说

（，）	输入	（，）输出
00	0	00
01	0	01
10	0	10
00	1	01
01	1	10
10	1	00

我们看到 有两个地方是1，用下面的表格举例子，求解新的

			，
1	0	0	10

先将 但是其值不等于 新 ，1 & 0 & 0 != 1，因此在相应部位添加 非运算 ，能够使的1 & ~0 & ~0 = 1，即对应部分如果是 0 就取反，多个是 1 的地方用运算符|表示。

👀因此不难计算出：

再比如有 4 个地方是 1，他们分别是

00      1     01        ~a & ~b &  c
01      1     11        ~a &  b &  c
01      0     01        ~a &  b & ~c
11      0     11         a &  b & ~c

所以

时间复杂度：，其中 为数组长度，只需要遍历一次数组。

空间复杂度：

🐛最优代码

public int singleNumber(int[] nums) {
    int a = 0, b = 0;
    for (int num : nums) {
        int tempa = ( a & ~b & ~num) | (~a &  b &  num);
        int tempb = (~a & ~b &  num) | (~a &  b & ~num); // 可以简化:a & (b^ num)
        a = tempa;
        b = tempb;
    }
    return b;
}

解4：只出现一次的数字 III

题目

给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。

进阶：你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现？

示例 1：

输入：nums = [1,2,1,3,2,5] 输出：[3,5] 解释：[5, 3] 也是有效的答案。

示例 2：

输入：nums = [-1,0] 输出：[-1,0]

示例 3：

输入：nums = [0,1] 输出：[1,0]

基础思路

我们可以使用一个哈希映射统计数组中每一个元素出现的次数。在统计完成后，我们对哈希映射进行遍历，将所有只出现了一次的数放入答案中。

时间复杂度：，其中 为数组长度

空间复杂度：，即为哈希映射需要使用的空间。

官方代码

class Solution {
    public int[] singleNumber(int[] nums) {
        Map<Integer, Integer> freq = new HashMap<Integer, Integer>();
        // 1. 统计次数
        for (int num : nums) {
            freq.put(num, freq.getOrDefault(num, 0) + 1);
        }
        int[] ans = new int[2];
        int index = 0;
        // 2. 查找2次
        for (Map.Entry<Integer, Integer> entry : freq.entrySet()) {
            if (entry.getValue() == 1) {
                ans[index++] = entry.getKey();
            }
        }
        return ans;
    }
}

思路

如果把 中的所有元素全部异或起来，其中出现一次的数为 和 ，得到结果 ，那么一定有：

其中 表示异或运算。这是因为 中出现偶数次的元素都会因为 被抵消掉，那么最终的结果就只剩下 和 的异或和。

🚩 显然不会等于 0，如果 ，那么说明 ，这样 和 就不是只出现一次的数字了。

🐛我们使用位运算 取出 的二进制表示中最低位的那个 ，设其为第 位， 和 异或和的第 位为 ，那么 和 中的必有一个数的二进制表示的第 位为 0，且另一个数的二进制表示的第 位为 1。因为只有在这种情况下，的二进制表示的第 位才能为 。

Tips：其实我们可以取任意的第 k 位，只要这一位二进制表示为 1 ，那么就可以用来区分

对于数组中所有出现为偶数次的元素来说，它们的二进制表示第 位只有两种可能性，要么为1要么为0，那么我们只需要将他们分成两组，第 位为1的一组，第 位为0的一组，对组内的所有元素求异或和，这样就能将两答案分到不同的组，且异或和就是答案 。

复杂度分析

时间复杂度：，其中 为数组长度

空间复杂度：

🚩官方代码

class Solution {
    public int[] singleNumber(int[] nums) {
        int xorsum = 0;
        for (int num : nums) {
            xorsum ^= num;
        }
        // 防止溢出
        int lsb = (xorsum == Integer.MIN_VALUE ? xorsum : xorsum & (-xorsum));
        int type1 = 0, type2 = 0;
        for (int num : nums) {
            if ((num & lsb) != 0) {
                type1 ^= num;
            } else {
                type2 ^= num;
            }
        }
        return new int[]{type1, type2};
    }
}