快排思想

快排类似铲土，把大于基准的铲到右边，小于基准的铲到左边，一次快排结束，会得到基准的正确位置。
其他元素的位置正不正确未知，接下来把基准两侧的数组，分别递归调用快排。直至所有元素归位

循环过程中**

先从 j 开始向左搜索，搜索比基准小的数字，**铲到 i 所在位置**
j 铲完，i开始向右搜索，搜索比基准大的数字，**铲到 j 所在的位置**
i，j 轮流互相铲“ 土元素 “，直至 i = j，**此位置放置基准**
一次循环结束

时间复杂度分析

最糟糕情况下时间复杂度是O(n²)

解释：基准取第一项时，是最糟的情况，完成每层需要的时间是 n，栈的高度是 n，时间复杂度就是n²

  - **备注：**第一项指的是基准取了**最小值 **[ **升序** ] 或者**最大值 **[ **降序** ]

平均的复杂度是O(nlogn)

解释：取中间值时候，完成每层的时间是n，调用栈的高度变成logn，这个时候时间复杂度是nlogn

  - **备注：**这里的 n 和 logn , 分别代表了**调用栈的高度**和**完成每层的时间**

快排铲土过程演示

                **起始数组**    ![image.png](https://cdn.nlark.com/yuque/0/2020/png/2955945/1608650012646-e4f459cb-b8b1-4692-81db-7d15fe61375c.png#align=left&display=inline&height=65&margin=%5Bobject%20Object%5D&name=image.png&originHeight=130&originWidth=772&size=17350&status=done&style=none&width=386)

j 从右边向左搜索，比基准小的数字，铲到 i 的位置

基准** -1**

i = j 搜索结束，将基准放入 i = j 位置

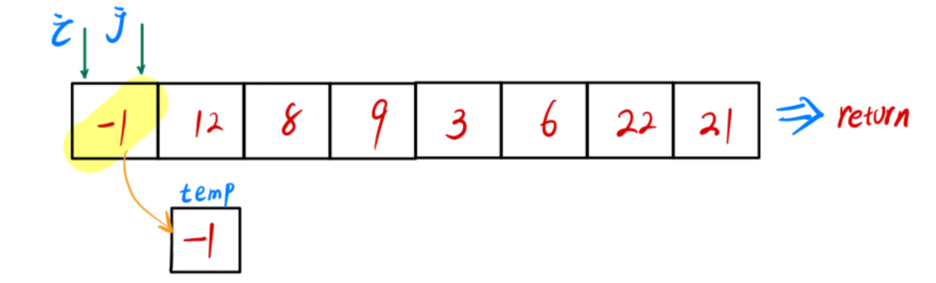
j 从右边向左搜索，比基准小的数字，铲到 i 的位置
**
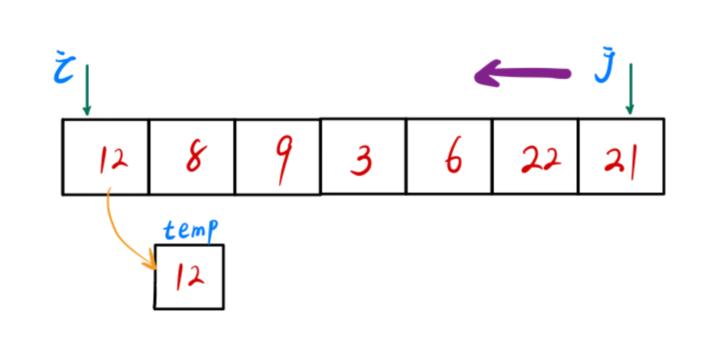2FT6$_20``(3%7]KC68F72I.png
j 铲到 i 的位置

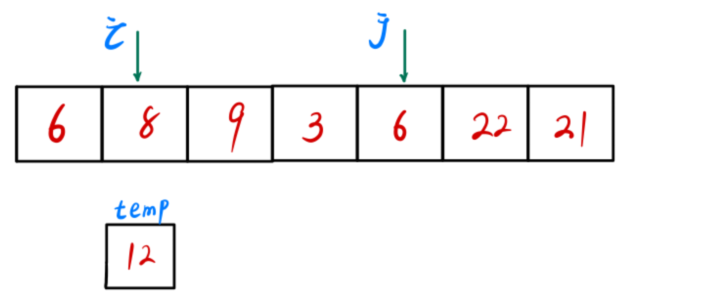
j 铲完，i 向右搜索，搜索比基准大的数字，铲到 j 处

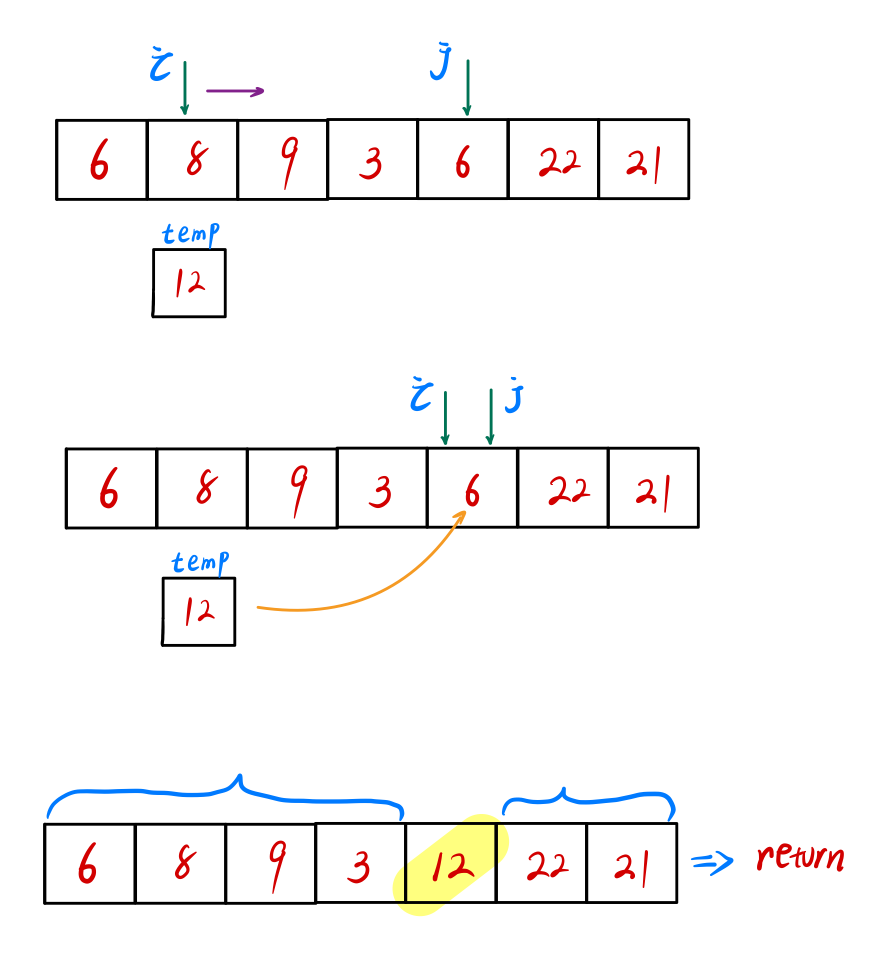
基准12位置正确**，因此将数组分成两部分，分别递归快排求解**

快排代码

铲土流快排代码

#include<iostream>
#pragma warning(disable:4996)
using namespace std;
//快速排序算法(从小到大)
//arr:需要排序的数组，begin:需要排序的区间左边界，end:需要排序的区间的右边界 [begin,end]
int partition(int arr[], int begin, int end) {
    int temp = arr[begin]; //将区间的第一个数作为基准数
    int i = begin; //从左到右进行查找时的“指针”，指示当前左位置
    int j = end;   //从右到左进行查找时的“指针”，指示当前右位置
    //不重复遍历
    while (i < j)
    {
        //当右边的数大于基准数时，略过，继续向左查找
        //不满足条件时跳出循环，此时的j对应的元素是小于基准元素的
        while (i<j && arr[j] > temp)
            j--;
        //将右边小于等于基准元素的数填入右边相应位置
        arr[i] = arr[j];
        //当左边的数小于等于基准数时，略过，继续向右查找
        //(重复的基准元素集合到左区间)
        //不满足条件时跳出循环，此时的i对应的元素是大于等于基准元素的
        while (i < j && arr[i] <= temp)
            i++;
        //将左边大于基准元素的数填入左边相应位置
        arr[j] = arr[i];
    }
    //将基准元素填入相应位置
    arr[i] = temp;
    //此时的i即为基准元素的位置
    return i;
}
void quickSort(int arr[], int begin, int end)
{
    //如果区间不只一个数
    if (begin < end)
    {    //获取基准的位置
        int i = partition(arr, begin, end);
        //对基准元素的左边子区间进行相似的快速排序
        quickSort(arr, begin, i - 1);
        //对基准元素的右边子区间进行相似的快速排序
        quickSort(arr, i + 1, end);
    }
    //如果区间只有一个数或者end>begein，则返回
    else
        return;
}
int main()
{
    int num[12] = { 23,45,17,11,13,89,72,26,3,17,11,13 };
    int n = sizeof(num) / sizeof(num[0]);//计算数组长度
    quickSort(num, 0, n - 1);
    cout << "排序后的数组为：" << endl;
    for (int i = 0; i < n; i++)
        cout << num[i] << ' ';
    cout << endl;
    system("pause");
    return 0;
}

🚩这种 Split 方式比较有趣，一个 for 循环到底，因此也放这里了
[ 解释 ] : 我的 Split** 就是互相来回铲土

下面解释这 Split 独特之处

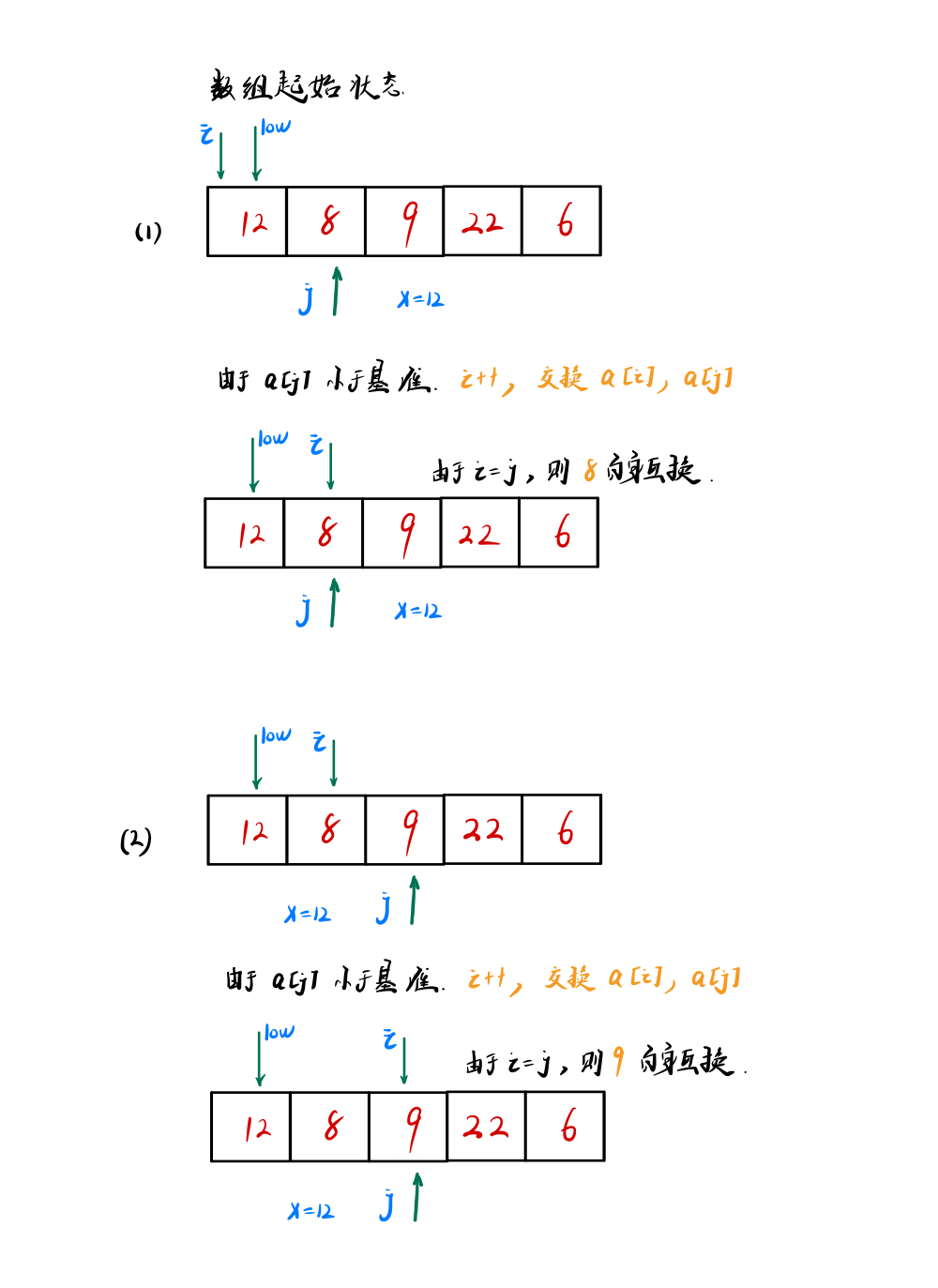
将首元素 nums[0]，当做基准
将 j 指针 从下标1开始移动至数组末尾，只处理比基准小的元素
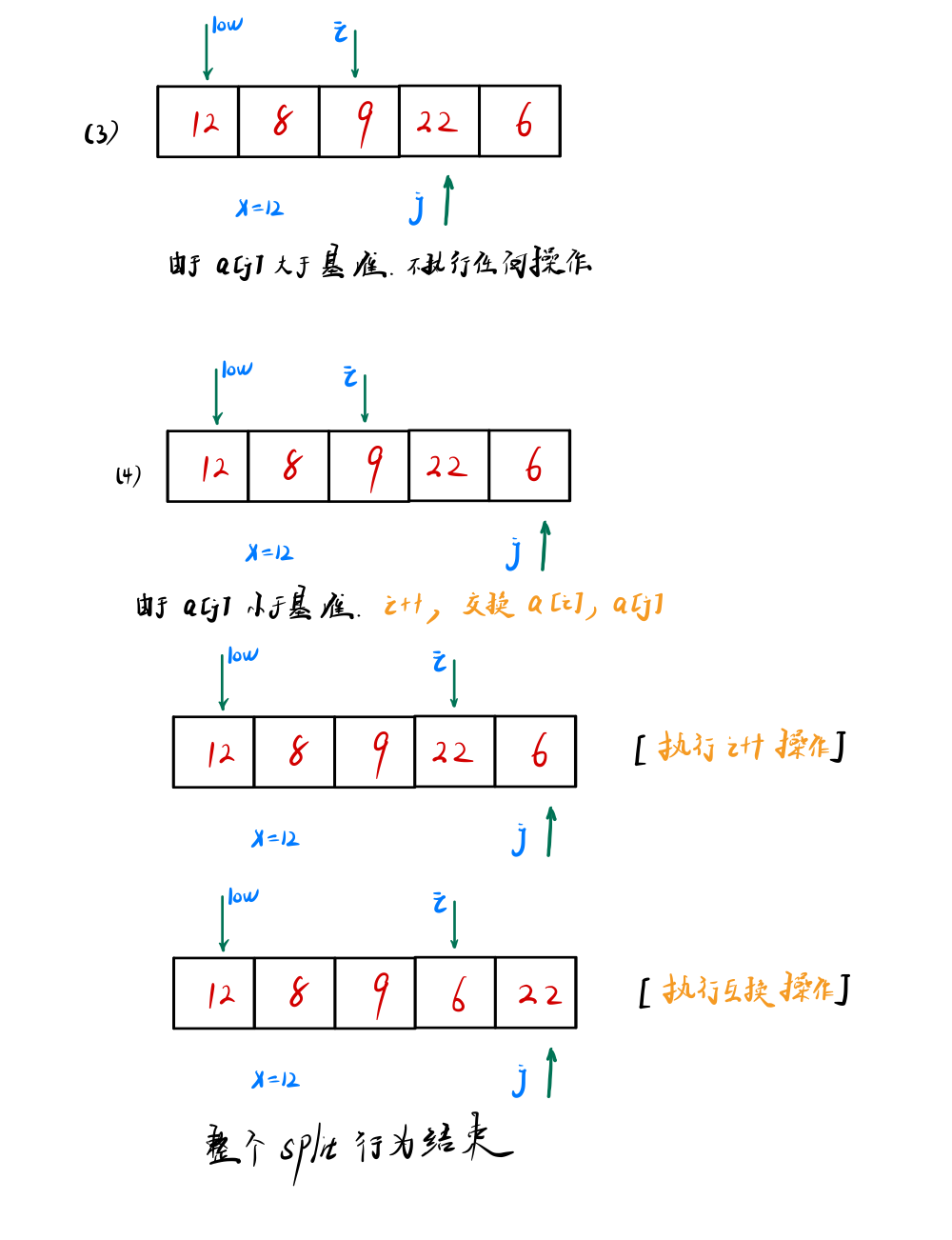
- 若 j 下标元素比基准小，则和 i++，swap( a[i] , a[j] )
循环交换 swap( a[low], a[i] )

🍖例子流程图

#include<stdio.h>
void swap(int &a, int &b)
{
    int t = a;
    a = b;
    b = t;
}
//划分数组的函数
int split(int a[], int low, int high)
{
    int i = low;    //i指向比较元素的期望位置
    int x = a[i];    //将该数组第一个元素设置为比较元素
    //从数组的第二个元素起开始遍历，若找到的元素大于比较元素，则跳过
    for(int j = low+1;j<=high;j++)
        //若找到了小于比较元素的数，则将其与前面较大的数进行交换
        if (a[j] <= x)
        {
            i++;
            swap(a[i], a[j]);
        }
    swap(a[low], a[i]);    //将比较元素交换到期望位置
    return i;
}
//快速排序
void quicksort(int a[], int low, int high)
{
    if (low < high)
    {
        int i = split(a, low, high);    //划分数组并获得比较元素位置
        quicksort(a, low, i - 1);    //对比较元素左边进行排序
        quicksort(a, i + 1, high);    //对比较元素右边进行排序
    }
}
int main()
{
    int a[] = { 5,7,1,6,4,8,3,2 };
    int length = sizeof(a) / sizeof(a[0]);
    quicksort(a, 0, length - 1);
    for (int i = 0; i < length; i++)
        printf("%d ", a[i]);
    printf("\n");
    return 0;
}

LeetCode

快排总结

快排思想

时间复杂度分析

快排铲土过程演示

快排代码