[NC]125. 和为 K 的连续子数组

🚩传送门：牛客题目
力扣题目

题目

给定一个整数数组和一个整数 ，请找到该数组中和为 的连续子数组的个数。

示例 1 :

输入:nums = [1,1,1], k = 2 输出: 2 解释: 此题 [1,1] 与 [1,1] 为两种不同的情况

示例 2 :

输入:nums = [1,2,3], k = 3 输出: 2

牛客求该数组中和为 的连续子数组的最大长度。
力扣求该数组中和为 的连续子数组的个数。

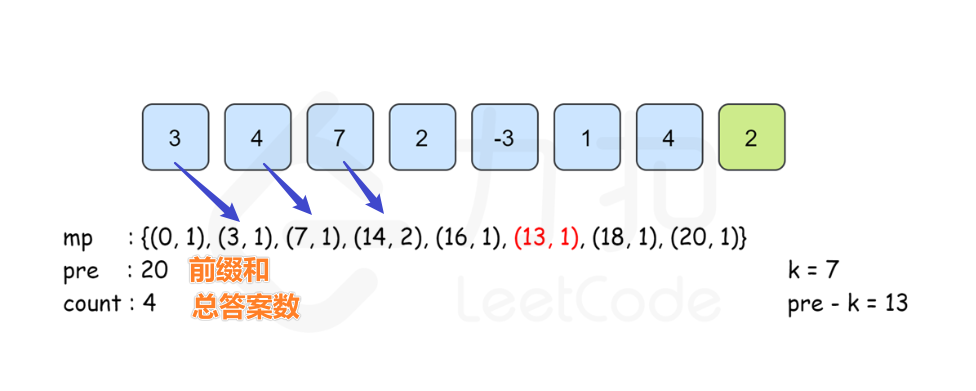
力扣思路：前缀和 + 哈希表优化

👉 定义： 为 里所有数的和，则 可以由 递推而来

那么「 这个子数组和为 」这个条件我们可以转化为

对于每个 我们需要从 中遍历，速度太慢，优化一下 将 存入 Hashmap 中

• ：为的值，即 里所有数的前缀和
• ：为个数，即 里所有数的和为的序列个数

  例如：[0，1] 、[0 ，1，2，-3] 前缀和都是 0 ，0 是做 key，2个序列数做 value

那么「 这个子数组和为 」这个条件我们可以转化为

我们只需要知道 中有多少个和为 的 就可以了

复杂度分析

时间复杂度： ，其中 是数组的长度，只需要遍历数组一次。中间利用哈希表查询删除的复杂度均为 。

空间复杂度： ，即为存储 所有状态使用的空间，哈希表在最坏情况下可能有 个不同的键值

我的代码

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int res = 0;
        int sum = 0;
        HashMap < Integer, Integer > mp = new HashMap < > ();
        mp.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            if (mp.containsKey(sum - k)) {
                res += mp.get(sum - k);
            }
            mp.put(sum, mp.getOrDefault(sum, 0) + 1);
        }
        return res;
    }
}

题目

给定一个整数数组和一个整数 ，请找到该数组中和为 的连续子数组的最大长度。

示例 1 :

输入:nums = [1,1,1], k = 2 输出: 2 解释: 此题 [1,1] 长度为 2

示例 2 :

输入:nums = [1,2,3], k = 3 输出: 2 解释: 此题 [1,2] 长度为 2

力扣思路：前缀和 + 哈希表优化

将 存入 Hashmap 中

• ：为的值，即 里所有数的前缀和

• ：为最小的下标，贪心思想：相同的 ，想让长度尽量的厂，其要尽量的小。

  public class Solution {
  
    public int maxlenEqualK (int[] arr, int k) {
        int res = 0;
        int sum = 0;
        HashMap < Integer, Integer > mp = new HashMap <> ();
        mp.put(0, -1);
        for (int i = 0; i < arr.length; i++) {
            sum += arr[i];
            if (mp.containsKey(sum - k)) {
                // 查看能否刷新答案
                res =Math.max(res,i-mp.get(sum - k));
            }
            // 如果已经存在就使用默认的,否则插入当前的i
            mp.put(sum, mp.getOrDefault(sum, i));
        }
        return res;
    }
  }