[NC]148. 几步可以从头跳到尾

🚩传送门：牛客题目

题目

给你一个长度为 的数组 。 表示从 这个位置开始最多能往后跳多少格 。求从 开始最少需要跳几次就能到达第 个格子 。
进阶： 空间复杂度 ， 时间复杂度 。

示例1:

输入：2,[1,2] 返回值：1 说明：从 1 号格子只需要跳跃一次就能到达 2 号格子

示例2:

输入：3,[2,3,1] 返回值：1 说明：从 1 号格子只需要跳一次就能直接抵达 3 号格子

解题思路：双指针

参数说明：

• _left_： 和 的边界
• _right_：的最右端边界
• _res：_保存需要返回的答案
• _[i,left]_ 区间的步长需要
• _[left,right]_ 区间的步长需要

算法说明：

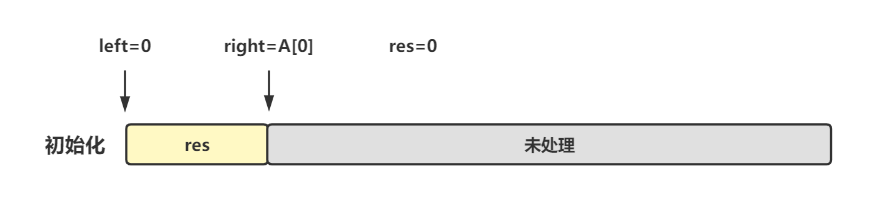
初始化内容：

指针**i** 从**0** 开始遍历至数组结尾。并查看自身当前位置所能跳到的最远距离（i+A[i]），看是否能刷新

• 不能刷新，则i继续遍历下一个位置
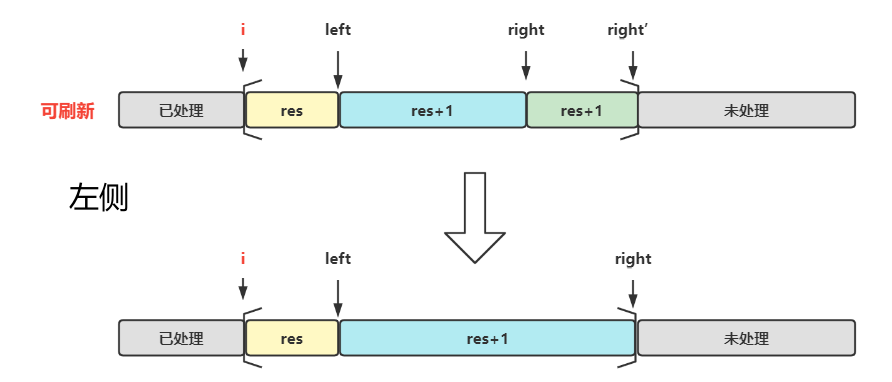
• 若能刷新，则查看当前 i 在 left 的左边还是右边
  • 左边：是说明跳跃到的地方所需步长依旧为 ，仅需要修改 指向最远边界即可
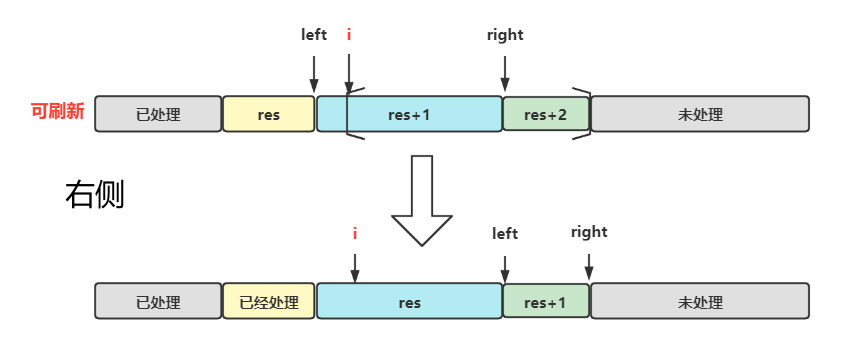
  • 右边：是说明跳跃到的地方所需步长更改为 ，此时需要修改 res，left，right

    、 、 **

图解说明：

1. 若不能刷新，无需任何操作，直接遍历查看下一个位置

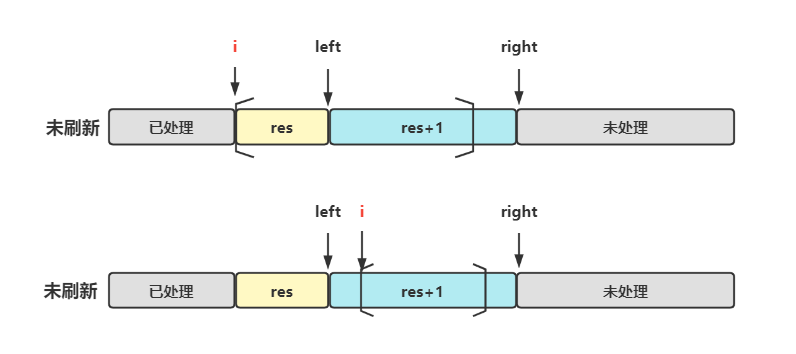
1. 若能刷新，则查看当前 i 在 left 的左边还是右边

复杂度分析

时间复杂度： ，该方法需要遍历一次数组所有元素 。

空间复杂度： ，该方法使用常数空间 。

我的代码

public int Jump (int n, int[] A) {
    int left=0,right=A[0],res=0;    //1. 初始化
    if(A[0]>n) return 1;
    for(int i=0;i<A.length;i++){
        if(i+A[i]>right){            //2. 可刷新
            if(i>left){                //3. i在left左侧
                res++;
                left=right;
                right=i+A[i];
            }else{                    //4. i在left右侧
                right=i+A[i];
            }
        }
    }
    return res;
}