🍗旋转数组问题合集

解1：[LC189]旋转数组

🚩传送门：力扣题目
给定一个数组，将数组中的元素向右移动 个位置，其中 是非负数。

进阶：

• 尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
• 你可以使用空间复杂度为 的 原地 算法解决这个问题吗 ？

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3 输出: [5,6,7,1,2,3,4] 解释: 向右旋转 1 步: [7,1,2,3,4,5,6] 向右旋转 2 步: [6,7,1,2,3,4,5] 向右旋转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2 输出：[3,99,-1,-100] 解释: 向右旋转 1 步: [99,-1,-100,3] 向右旋转 2 步: [3,99,-1,-100]

解题思路：环状替换

我们可以使用额外的数组来将每个元素放至正确的位置。使用额外数组的原因在于如果我们直接将每个数字放至它最后的位置，这样被放置位置的元素会被覆盖从而丢失。因此，从另一个角度，我们可以将被替换的元素保存在变量 temp 中，从而避免了额外数组的开销。

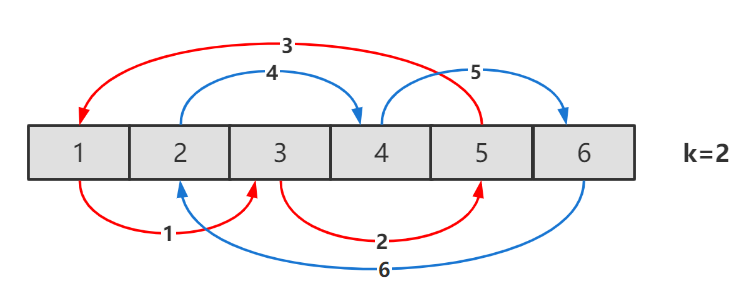
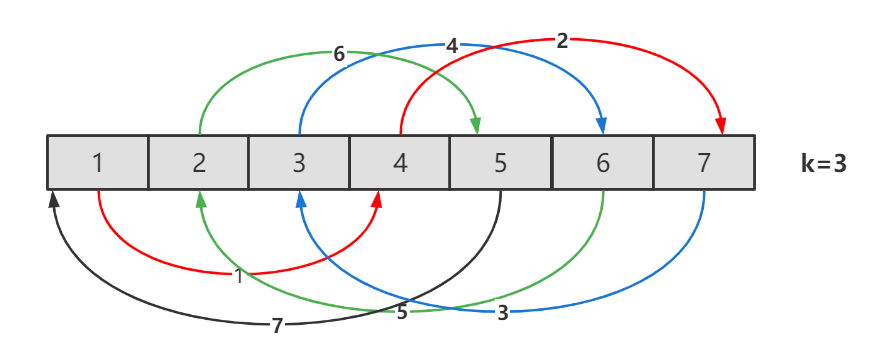
从位置 0 开始，最初令temp=nums[0]。根据规则，位置 0 的元素会放至 x=(0+k) mod n 的位置，此时交换 temp 和 nums[x]，完成位置 x 的更新。然后，我们考察位置 x，并交换 temp 和 nums[(x+k)modn]，从而完成下一个位置的更新。不断进行上述过程，直至回到初始位置 0。

容易发现，当回到初始位置 0 时，有些数字可能还没有遍历到，此时我们应该从下一个数字开始重复的过程。

可是这个时候怎么才算遍历结束呢 ？

我们不妨先考虑这样一个问题：对于 n 个元素的数组，只需要交换 n 次
其实循环的起点个数是 n 和 k 的最小公约数

复杂度分析

时间复杂度：，其中 为数组的长度。每个元素只会被遍历一次。

空间复杂度：，我们只需常数空间存放若干变量。

我的代码

class Solution {
    // usage: y = swap(x, x=y);
    public static int swap(int a, int b) {  
        return a;
    }

    //我们知道只需要交换n次就可以终止
    public void rotate(int[] nums, int k) {  
        int n=nums.length;
        for(int i=0;i<k;i++){
            int temp=nums[i];
            int x=(i+k)%nums.length;
            while(x!=i){
                nums[x]=swap(temp,temp=nums[x]);
                //每交换一次就统计是否需要终止
                if(--n==0)return ;
                x=(x+k)%nums.length;
            }
            nums[i]=temp;
            //每交换一次就统计是否需要终止
            if(--n==0)return ;
        }
    }
}

解题思路：数组翻转

该方法基于如下的事实：当我们将数组的元素向右移动 k 次后，尾部 k mod n 个元素会移动至数组头部，其余元素向后移动 k mod n 个位置。

该方法为数组的翻转：

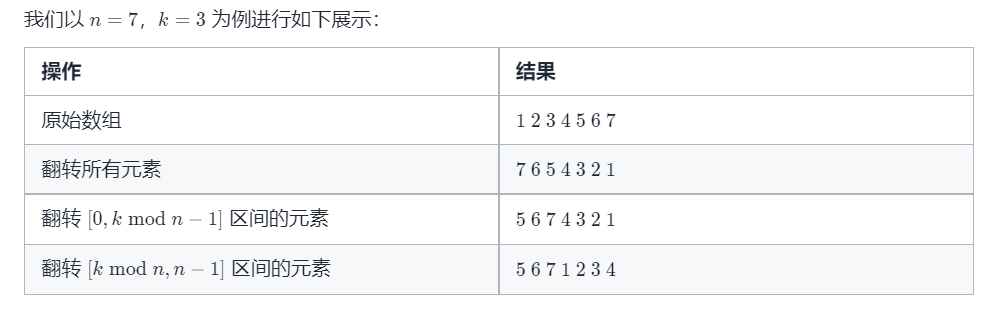
     1. 我们可以先将所有元素翻转，这样尾部的 **k mod n** 个元素就被移至数组头部
     1. 再翻转 **[0,k mod n−1]** 区间的元素
     1. 再翻转 **[k mod n,n−1]** 区间的元素即能得到最后的答案。

算法解释：

nums = “——->—>”; k =3 result = “—>——->”;

reverse “——->—>” we can get “<—<——-“ reverse “<—“ we can get “—><——-“ reverse “<——-“ we can get “—>——->” this visualization help me figure it out :

复杂度分析

时间复杂度：，其中 为数组的长度。

  - 每个元素被翻转两次，一共 **n** 个元素

空间复杂度：，我们只需常数空间存放若干变量。

我的代码

class Solution {
    public void rotate(int[] nums, int k) {
        k %= nums.length;
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }

    public void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start += 1;
            end -= 1;
        }
    }
}

解2：[LC153]寻找旋转排序数组中的最小值

🚩传送门：力扣题目
已知一个长度为 的数组，预先按照升序排列，经由 到 次 旋转 后，得到输入数组。
例如：原数组 在变化后可能得到：

  - 若旋转 4 次，则可以得到 `[4,5,6,7,0,1,2]`
  - 若旋转 7 次，则可以得到 `[0,1,2,4,5,6,7]`

注意：数组 旋转一次 的结果为数组

给你一个元素值 互不相同 的数组 ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

示例 1：

输入：nums = [3,4,5,1,2] 输出：1 解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2] 输出：0 解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17] 输出：11 解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

解题思路：二分查找 [基本有序就可使用]

一个不包含重复元素的升序数组在经过旋转之后，可以得到下面可视化的折线图：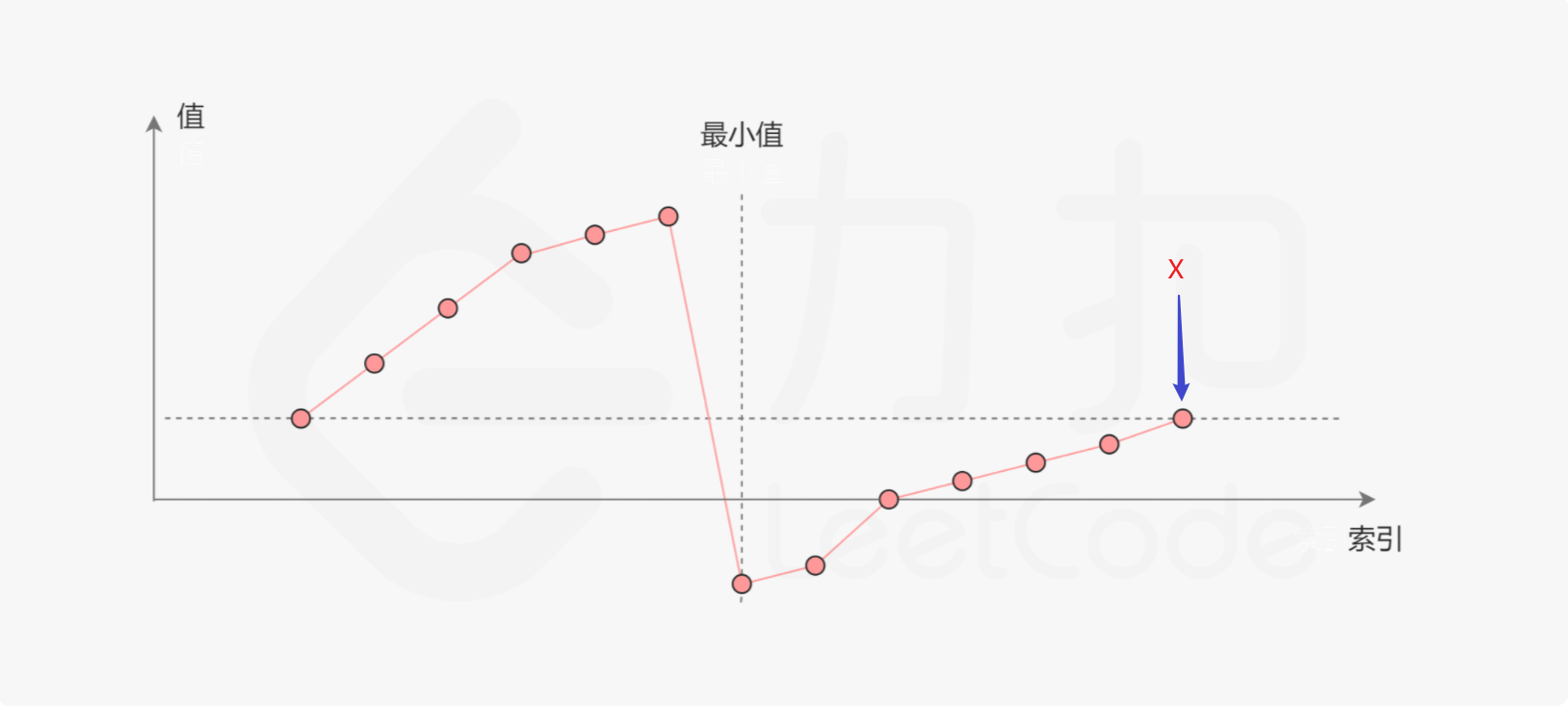

横轴表示数组元素的下标，纵轴表示数组元素的值。图中标出了最小值的位置，是我们需要查找的目标。

我们考虑数组中的最后一个元素 x ：

1. 在最小值右侧的元素（不包括最后一个元素本身），它们的值一定都严格小于 x；
2. 在最小值左侧的元素，它们的值一定都严格大于 x 。

因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。

在二分查找的每一步中，左边界为 ，右边界为 ，区间的中点为 ，最小值就在该区间内。

我们将中轴元素 与右边界元素 进行比较，可能会有以下的三种情况：

1. 第一种情况是 。

如下图所示，这说明 是最小值右侧的元素，因此我们可以忽略二分查找区间的右半部分。

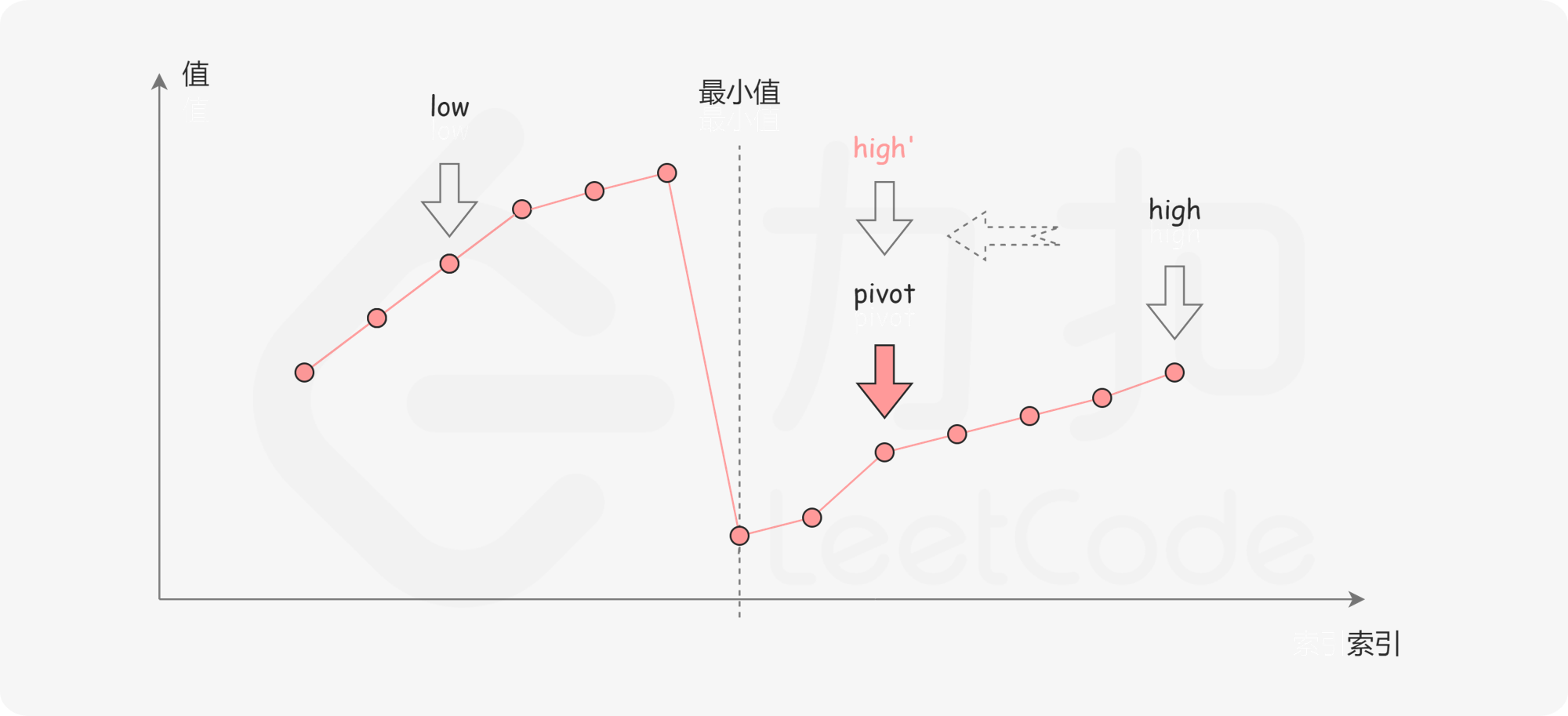
为什么 high = pivot 而不是 high = pivot-1 ？

万一pivot指向的是最小值，有可能会丢失。

1. 第二种情况是 。

如下图所示，这说明 是最小值左侧的元素，因此我们可以忽略二分查找区间的左半部分。

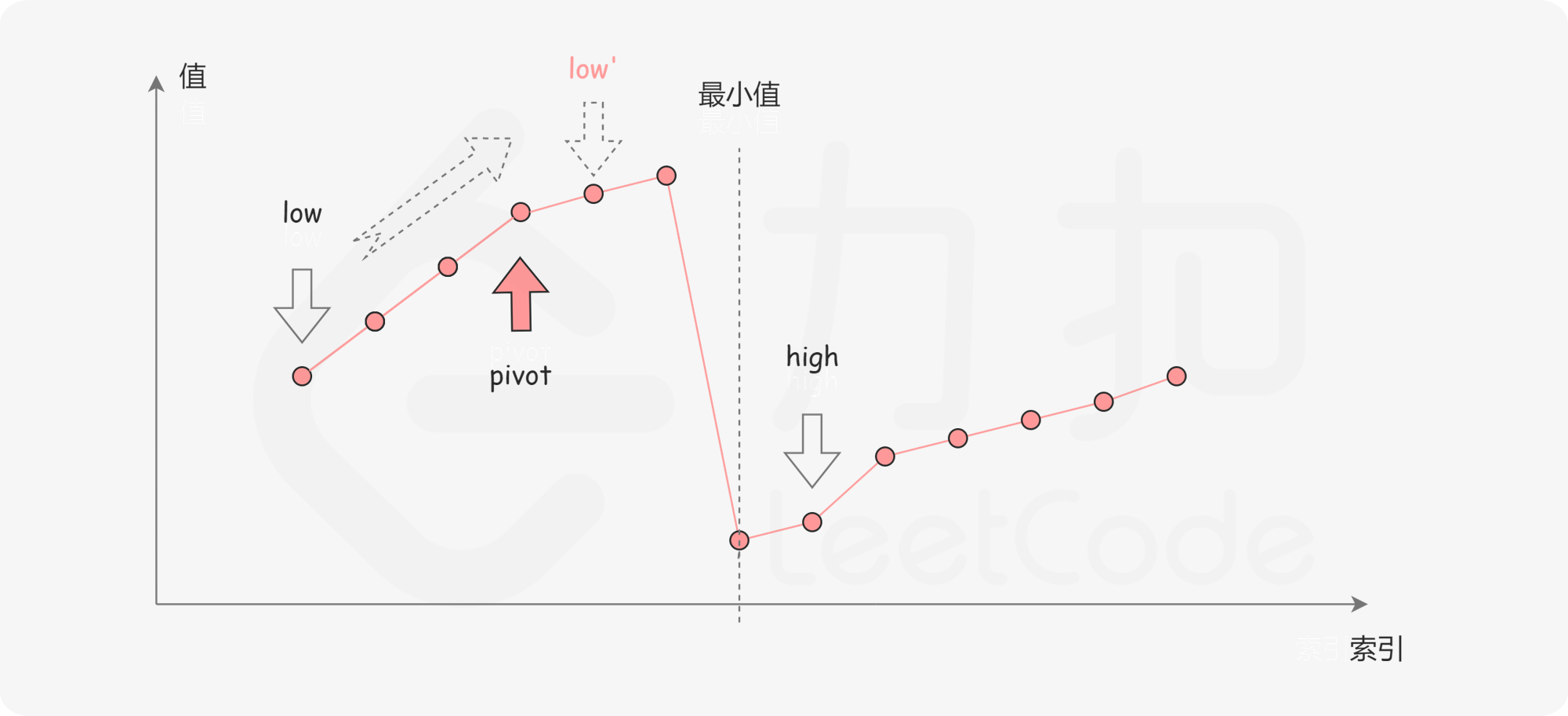
为什么 **low = pivot+1** 而不是 **low = pivot** ？

因为不会丢失最小值数据，pivot 一定不是最小值，因为 min<high<pivot

由于数组不包含重复元素，并且只要当前的区间长度不为 1， 就不会与 重合；而如果当前的区间长度为 1，这说明我们已经可以结束二分查找了。因此不会存在 的情况。

当二分查找结束时，我们就得到了最小值所在的位置。

复杂度分析

时间复杂度：，其中 为数组 的长度。二分查找的过程中，每一步会忽略一半的区间。

空间复杂度：

我的代码

class Solution {
    public int findMin(int[] nums) {
        int low = 0;
        int high = nums.length - 1;
        while (low < high) {
            int pivot = (low + high) / 2;
            if (nums[pivot] < nums[high]) {
                high = pivot;
            } else {
                low = pivot + 1;
            }
        }
        return nums[low];
    }
}

解惑：为什么while的条件是low<high,而不是low<=high呢？

解答：假如最后循环到长度为2的{10,1}的这种情况 nums[low]=10、nums[high]=1、nums[mid]=10，此时由于nums[low]=10>nums[high]=1故而low会修改为mid+1,此时low指向的就是最小值的下标，可以直接可以跳出循环了。

解3：[LC154] 寻找旋转排序数组中的最小值 II

🚩传送门：力扣题目
已知一个长度为 的数组，预先按照升序排列，经由 到 次 旋转 后，得到输入数组。
例如：原数组 在变化后可能得到：

  - 若旋转 4 次，则可以得到 `[4,5,6,7,0,1,2]`
  - 若旋转 7 次，则可以得到 `[0,1,2,4,5,6,7]`

注意：数组 旋转一次 的结果为数组

给你一个可能存在 重复 元素值的数组 ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

示例 1：

输入：nums = [1,3,5] 输出：1

示例 2：

输入：nums = [2,2,2,0,1] 输出：0

解题思路：二分查找 [基本有序就可使用]

一个包含重复元素的升序数组在经过旋转之后，可以得到下面可视化的折线图：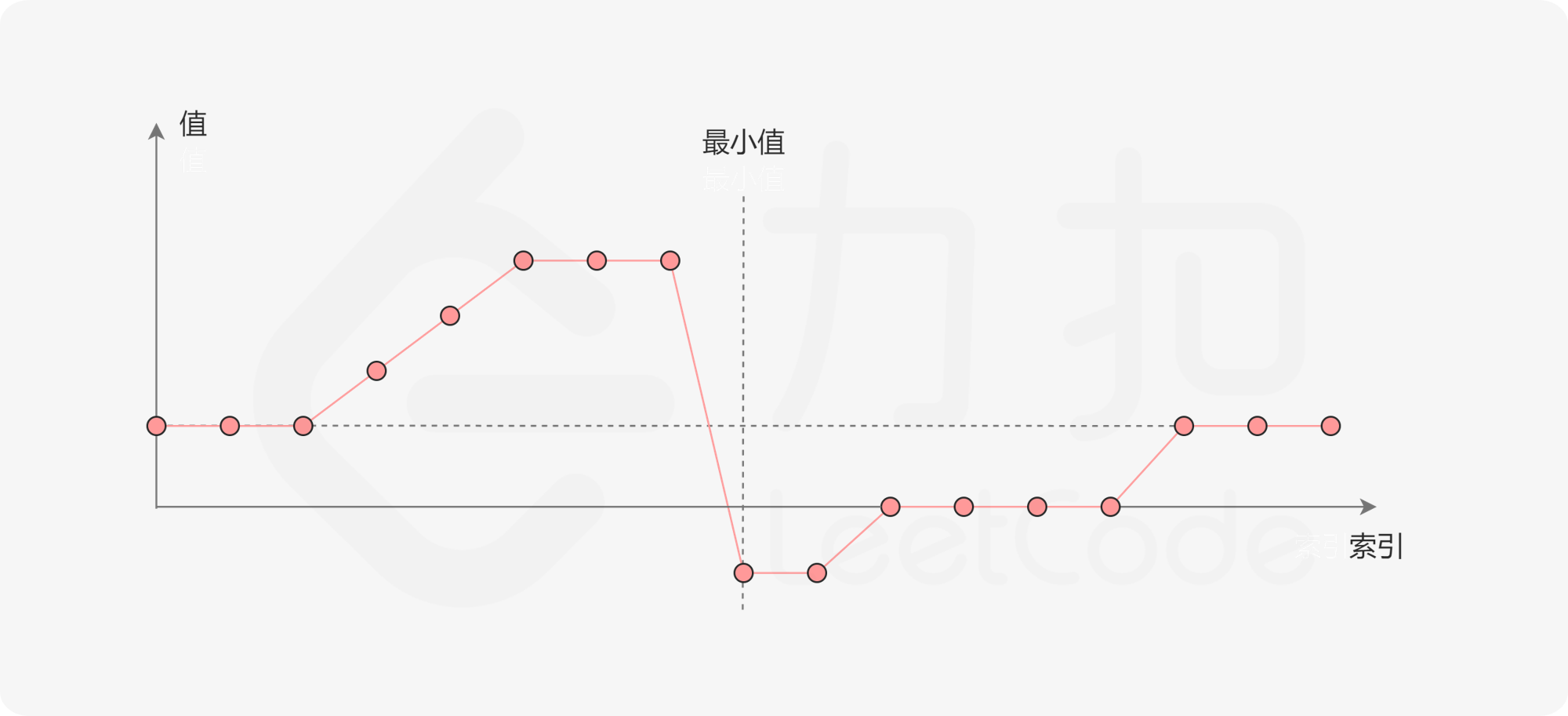

横轴表示数组元素的下标，纵轴表示数组元素的值。图中标出了最小值的位置，是我们需要查找的目标。

我们考虑数组中的最后一个元素 x ：

1. 在最小值右侧的元素（不包括最后一个元素本身），它们的值一定都严格小于 x；
2. 在最小值左侧的元素，它们的值一定都严格大于 x 。

因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。

在二分查找的每一步中，左边界为 ，右边界为 ，区间的中点为 ，最小值就在该区间内。

我们将中轴元素 与右边界元素 进行比较，可能会有以下的三种情况：

1. 第一种情况是 。

如下图所示，这说明 是最小值右侧的元素，因此我们可以忽略二分查找区间的右半部分。

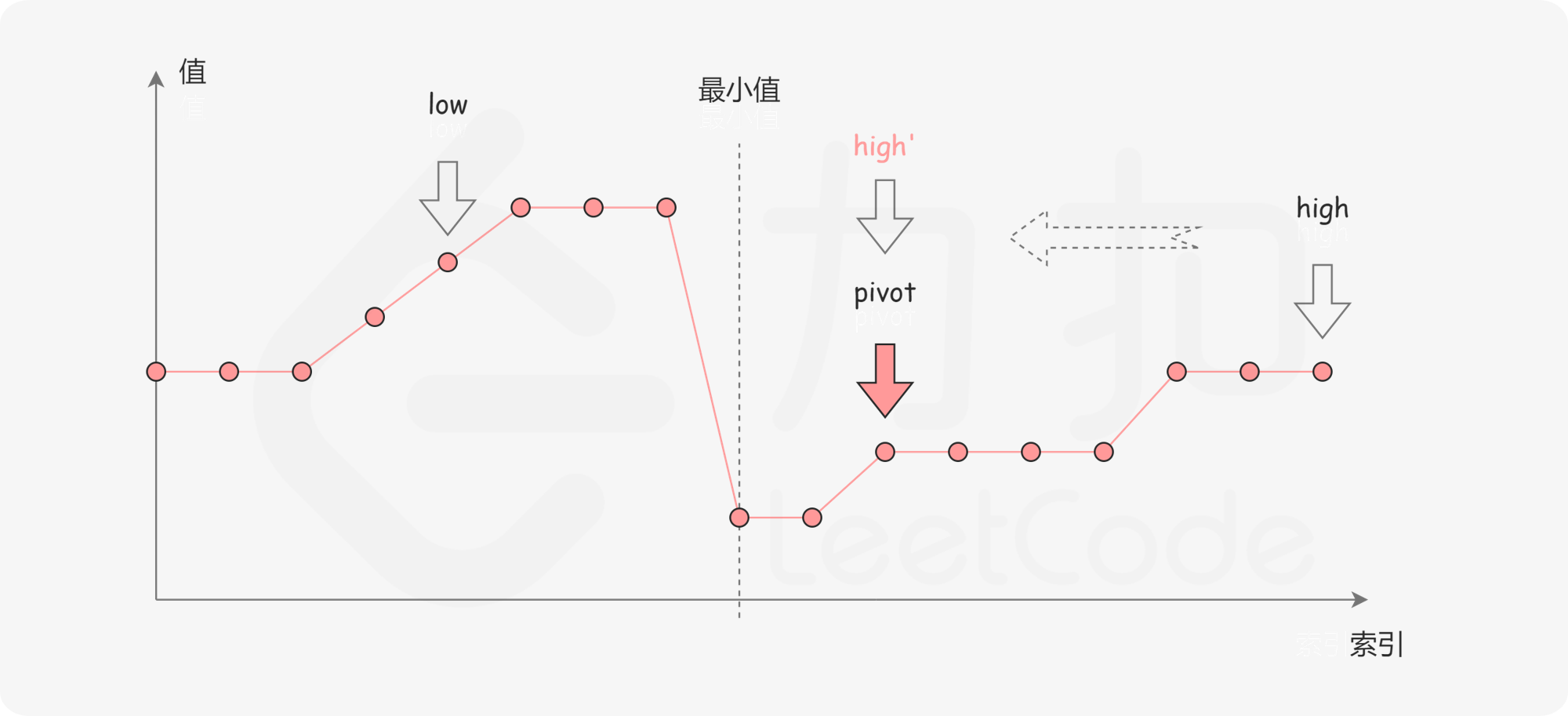
1. 第二种情况是 。

如下图所示，这说明 是最小值左侧的元素，因此我们可以忽略二分查找区间的左半部分。

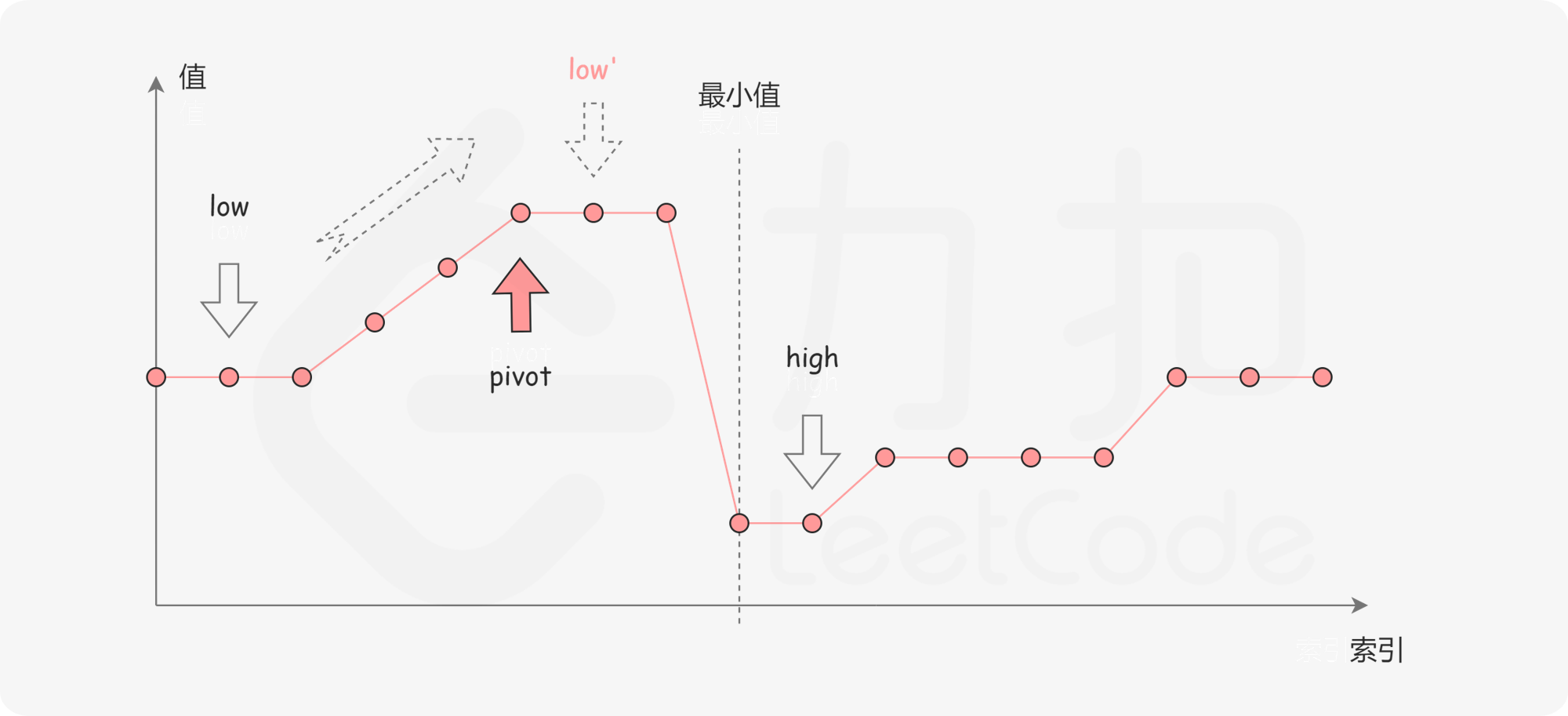
1. 第三种情况是 。

如下图所示，由于重复元素的存在，我们并不能确定 究竟在最小值的左侧还是右侧，因此我们不能莽撞地忽略某一部分的元素。我们唯一可以知道的是，由于它们的值相同，所以无论 是不是最小值，都有一个它的「替代品」 ，因此我们可以忽略二分查找区间的右端点。

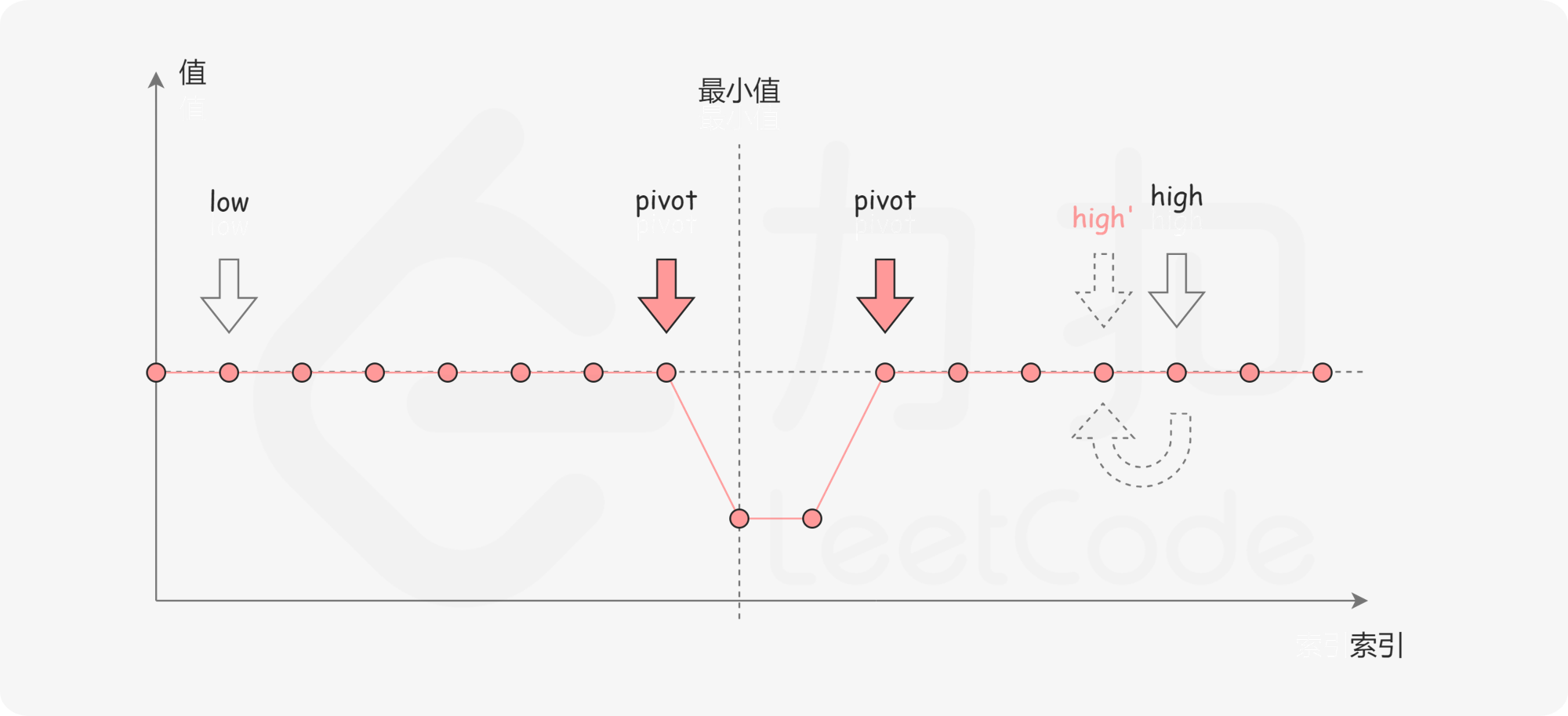
当二分查找结束时，我们就得到了最小值所在的位置。

复杂度分析

时间复杂度：，其中 为数组 的长度。

  - 若数组是随机生成的，那么数组中包含相同元素的概率很低，在二分查找的过程中，大部分情况都会忽略一半的区间。而在最坏情况下，如果数组中的元素完全相同，那么 **while **就需要执行 **n **次，每次忽略区间的右端点，时间复杂度为 ![](https://cdn.nlark.com/yuque/__latex/bf7c2e3ac858e1c3496fd2f47a300139.svg#card=math&code=%5Csmall%20O%28n%29&height=23&id=Txl0b)

空间复杂度：

我的代码

class Solution {
    public int findMin(int[] nums) {
        int low = 0;
        int high = nums.length - 1;
        while (low < high) {
            int pivot = low + (high - low) / 2;
            if (nums[pivot] < nums[high]) {
                high = pivot;
            } else if (nums[pivot] > nums[high]) {
                low = pivot + 1;
            } else {
                high -= 1;
            }
        }
        return nums[low];
    }
}

解4：[LC33] 搜索旋转排序数组 （非重元素）

🚩传送门：力扣题目

整数数组 按升序排列，数组中的值 互不相同 。

在传递给函数之前，在预先未知的某个下标 （）上进行了 旋转，使数组变为 （下标 从 开始 计数）。

例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为[4,5,6,7,0,1,2]。

给你 旋转后 的数组 和一个整数 ，若数组存在目标值 ，则返回它的下标，否则返回 。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0 输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3 输出：-1

示例 3：

输入：nums = [1], target = 0 输出：-1

解题思路：二分查找 [基本有序就可使用]

将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。 此时有序部分用二分法查找。无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。就这样循环.

对于有序数组，可以使用二分查找的方法查找元素。

但是这道题中，数组本身不是有序的，进行旋转后只保证了数组是局部有序的，这还能进行二分查找吗？可以的

可以发现的是，我们将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的。

拿示例来看，我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分，其中的左边 [4, 5, 6] 这个部分的数组是有序的，其他也是如此。

这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的，并根据有序的那个部分确定我们该如何改变二分查找的上下界，因为我们能够根据有序的那部分判断出 target 在不在这个部分：

1. 如果 [l, mid - 1] 是有序数组，且 target 的大小满足
   • 则将搜索范围缩小至 [l, mid - 1]，否则在 [mid + 1, r] 中寻找。
2. 如果 [mid, r] 是有序数组，且 target 的大小满足
   • 则将搜索范围缩小至 [mid + 1, r]，否则在 [l, mid - 1] 中寻找。

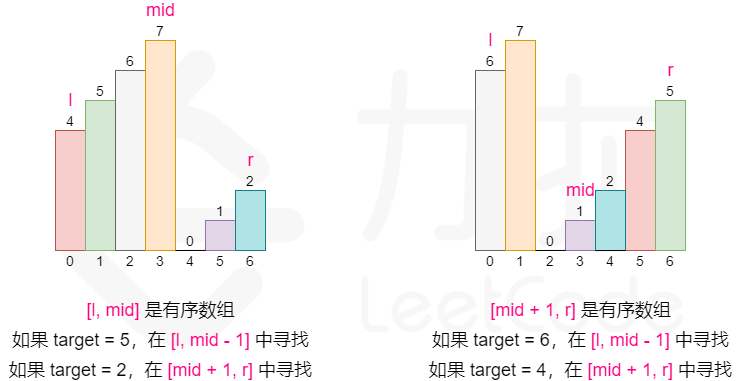
注意：二分的写法有很多种，所以在判断 target 大小与有序部分的关系的时候可能会出现细节上的差别。

复杂度分析

时间复杂度：，其中 为数组 的长度。

  - 整个算法时间复杂度即为二分查找的时间复杂度

空间复杂度：，我们只需要常数级别的空间存放变量。

我的代码

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        if (n == 0) return -1;
        if (n == 1)  return nums[0] == target ? 0 : -1;
        int l = 0, r = n - 1;
        # 这里控制条件取等号，取等号大多是为了在while中直return mid，不取等号就跳出while返回l的值。
        while (l <= r) {
            int mid = (l + r) / 2;
            # 中间值即为target，直接返回
            if (nums[mid] == target) return mid;
            # 左半部分是有序
            if (nums[l] <= nums[mid]) {
                # target落在左半部分有序区域内
                if (nums[l] <= target && target < nums[mid]) 
                    r = mid - 1;
                else 
                    # target落在右半部分无序区域内
                    l = mid + 1;
            }
            # 右半部分是有序
            else {
                # target落在右半部分有序区域内
                if (nums[mid] < target && target <= nums[n - 1]) 
                    l = mid + 1;
                else 
                    # target落在左半部分无序区域内
                    r = mid - 1;
            }
        }
        return -1;
    }
}

解5：[LC81] 搜索旋转排序数组II （重复元素）

🚩传送门：力扣题目
已知存在一个按非降序排列的整数数组 nums ，数组中的值 可以重复 。

在传递给函数之前，nums 在预先未知的某个下标 k（）上进行了 旋转，使数组变为 （下标 从 0 开始 计数）。

例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为[4,5,6,6,7,0,1,2,4,4]。

给你 旋转后 的数组 nums 和一个整数 target ，若数组存在目标值 target ，则返回 true，否则返回 false 。

示例 1：

输入：nums = [2,5,6,0,0,1,2], target = 0 输出：true

示例 2：

输入：nums = [2,5,6,0,0,1,2], target = 3 输出：false

解题思路：二分查找 [基本有序就可使用]

数组中有重复元素的情况，二分查找时可能会有
此时无法判断区间 [l,mid] 和区间 [mid+1,r] 哪个是有序的。
对于这种情况，我们只能将当前二分区间的左边界加一，右边界减一，然后在新区间上继续二分查找。

例如 nums=[3,1,2,3,3,3,3]，target=2，首次二分时无法判断区间 [0,3] 和区间 [4,6] 哪个是有序的。缩小边界

虽不知道那边有序，但是我们知道，答案肯定不是 nums[l] 和 nums[r]

复杂度分析

时间复杂度：，其中 为数组 的长度。

  - 最坏情况下数组元素均相等且不为 _**target**_，我们需要访问所有位置才能得出结果。

空间复杂度：，我们只需要常数级别的空间存放变量。

我的代码

class Solution {
    public boolean search(int[] nums, int target) {
        int n = nums.length;
        if (n == 0) {
            return false;
        }
        if (n == 1) {
            return nums[0] == target;
        }
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            if (nums[mid] == target) {
                return true;
            }
            //比问题4:多了一个特殊情况
            if (nums[l] == nums[mid] && nums[mid] == nums[r]) {
                ++l;
                --r;
            } else if (nums[l] <= nums[mid]) {
                if (nums[l] <= target && target < nums[mid]) {
                    r = mid - 1;
                } else {
                    l = mid + 1;
                }
            } else {
                if (nums[mid] < target && target <= nums[n - 1]) {
                    l = mid + 1;
                } else {
                    r = mid - 1;
                }
            }
        }
        return false;
    }
}

解6：[面试题 10.03] 搜索旋转数组

🚩传送门：力扣题目
搜索旋转数组。给定一个排序后的数组，包含 n 个整数，但这个数组已被旋转过很多次了，次数不详。

找出数组中的某个元素，假设数组元素原先是按升序排列的。若有多个相同元素，返回索引值最小的一个。

示例1:

输入: arr = [15, 16, 19, 20, 25, 1, 3, 4, 5, 7, 10, 14], target = 5 输出: 8（元素5在该数组中的索引）

示例2:

输入：arr = [15, 16, 19, 20, 25, 1, 3, 4, 5, 7, 10, 14], target = 11 输出：-1 （没有找到）

解题思路：二分查找 [基本有序就可使用]

1. nums[l]==target 直接返回, 因为 left 找的是最小的索引

2. nums[mid] == target 当中间值等于目标值，将右边界移到中间，因为左边可能还有相等的值

   如果 r=mid-1 则会丢失 r=mid 的信息

3. nums[l]<nums[mid] 左区间有序，target 在左区间就去左区间，不在就去右区间

4. nums[l]>nums[mid] 右区间有序，target 在右区间就去右区间，不在就去左区间
5. nums[l]=nums[mid] 当中间数字与左边数字相等时，将左边界右移

复杂度分析

时间复杂度：，其中 为数组 的长度。

  - 最坏情况下数组元素均相等且不为 _**target**_，我们需要访问所有位置才能得出结果。

空间复杂度：，我们只需要常数级别的空间存放变量。

我的代码

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        if (n == 0) return -1;
        if (n == 1) return nums[0] == target?0:-1;
        int l = 0 , r = n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            # 重点1：当left符合时直接返回, 因为找的是最小的索引
            if(nums[l]==target)
                return l;
            # 重点2：当中间值等于目标值，将右边界移到中间，因为左边可能还有相等的值
            if (nums[mid] == target){
                r=mid;
            }
            //左区间有序
            else if (nums[l]<nums[mid]){
                //目标值在左区间
                if (nums[l] <= target && target < nums[mid]) 
                    r = mid - 1;
                //目标值在右区间
                else 
                    l = mid + 1;
            }
            //右区间有序
            else if(nums[l]>nums[mid]){
                //目标值在右区间
                if (nums[mid] < target && target <= nums[n - 1]) 
                    l = mid + 1;
                //目标值在左区间
                else 
                    r = mid - 1;
            }
            # 重点3：当中间数字与左边数字相等时，将左边界右移
            else
                l++;
        }
        return -1;
    }
}

题目4，题目5，题目6，通解：

题目 6 的代码可以 解题目 4 ，题目 5

可以解非重复、重复元素的 target  
public int search (int[] nums, int target) {
        // write code here
        if(nums.length==0)return -1;
        if(nums.length==1)return nums[0]==target?0:-1;
        int n=nums.length,l=0,r=n-1;
        while(l<=r){
            int mid=l+(r-l)/2;
            if(nums[l]==target)return l;
            if(nums[mid]==target) r=mid;
            else if(nums[l]<nums[mid]){//左边有序
                if(nums[l]<=target&&target<nums[mid])//在左区间
                    r=mid-1;
                else 
                    l=mid+1;
            }
            else if(nums[l]>nums[mid]){//右区间有序
                if(nums[mid]<target&&target<=nums[r])//在右区间
                    l=mid+1;
                else
                    r=mid-1;
            }
            else //nums[l]==nums[mid]
                l++;
        }
        return -1;
    }
}