🚩传送门：牛客题目

题目

给出一组区间，请合并所有重叠的区间。请保证合并后的区间按区间起点升序排列。

要求：空间复杂度 [NC]37. 合并区间 - 图1，时间复杂度 [NC]37. 合并区间 - 图2
进阶：空间复杂度 [NC]37. 合并区间 - 图3，时间复杂度 [NC]37. 合并区间 - 图4

解题思路：双指针

对原区间进行排序，按照 [NC]37. 合并区间 - 图5 升序， [NC]37. 合并区间 - 图6 相等按 [NC]37. 合并区间 - 图7 升序 。

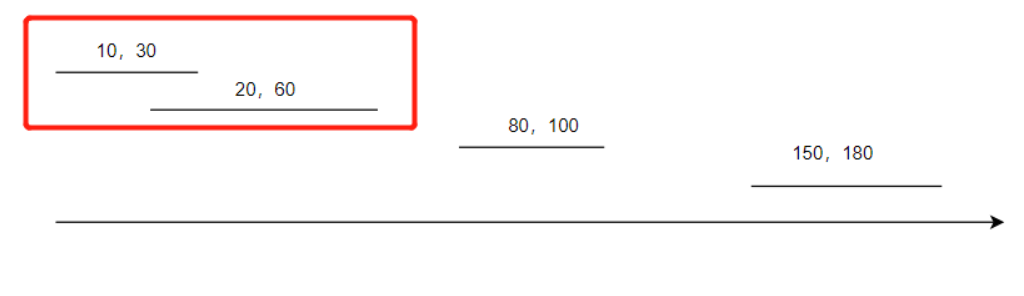
  • **后 start <= 前 end** 说明可以合并，合并后需要确定 **新end**

    例如： 后20 < 前30 ，需要确定 新end 是因为若前区间是 [10,60] 后区间是 [20,30] ，则新区间[10,60]

  • 不可以合并，已合并的存入答案集合，当前区间成为 **新start**和 **新end**

    例如：后80 > 前60，则 [10,60] 存入答案，80 成为 新 start ，100 成为 新 end

image.png

复杂度分析

时间复杂度：[NC]37. 合并区间 - 图9，其中 [NC]37. 合并区间 - 图10 为区间数量。

  1.   - 除去排序的开销，我们只需要一次线性扫描，所以主要的时间开销是排序的

空间复杂度：[NC]37. 合并区间 - 图11，其中 [NC]37. 合并区间 - 图12 为合并完成后的区间数

  1.   - 这里计算的是存储答案之外，使用的额外空间。![](https://cdn.nlark.com/yuque/__latex/0088a3edf69d254b157c0266960eded3.svg#card=math&code=O%28log%5C%20n%29&height=20&id=fnLbP)为排序所需要的空间复杂度

我的代码

public class Solution {
    //#区间类
    public class Interval {
        int start;
        int end;

        Interval() {
            start = 0;
            end = 0;
        }

        Interval(int s, int e) {
            start = s;
            end = e;
        }
    }
    //#合并函数
    public ArrayList<Interval> merge(ArrayList<Interval> intervals) {
        //1. 存储合并后答案的集合
        ArrayList<Interval> res = new ArrayList<>();
        //2. 判空操作
        if (intervals == null || intervals.size() == 0) return res;
        //3. 对原区间进行排序,按照start升序,start相等按end升序
        Collections.sort(intervals, new Comparator<Interval>() {
            @Override
            public int compare(Interval o1, Interval o2) {
                if (o1.start == o2.start) {
                    return o1.end - o2.end;
                }
                return o1.start - o2.start;
            }
        });
        int start = intervals.get(0).start;
        int end = intervals.get(0).end;
        //4. 后start<前end 说明可以合并
        for (int i = 1; i < intervals.size(); i++) {
            if (intervals.get(i).start <= end)
                end = Math.max(end, intervals.get(i).end); //可以合并需要确定新的end
            else {    //不可以合并,已合并的存入答案集合
                res.add(new Interval(start, end));
                start = intervals.get(i).start;
                end = intervals.get(i).end;
            }
        }
        res.add(new Interval(start, end));
        return res;
    }
}