[NC]246. 杨辉三角 II

🚩传送门：牛客题目
力扣题目

题目

给定一个非负索引 ，其中 ，返回杨辉三角的第 行。

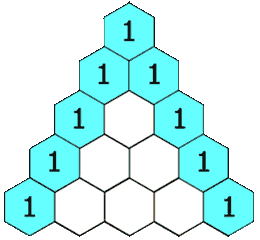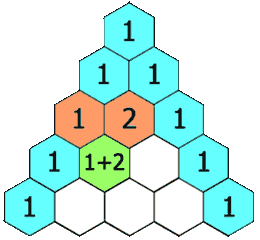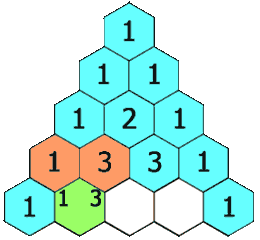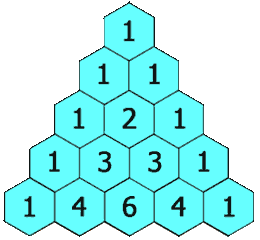
在杨辉三角中，每个数是它左上方和右上方的数的和。

示例：

输入：3 输出：[1,3,3,1]

进阶：
你可以优化你的算法到 空间复杂度吗？

解题思路：递推

根据杨辉三角性质，第 行的第 个数等于第 行的第 个数和第 个数之和。即 ，可以线性递推

初始版本代码

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<List<Integer>> C = new ArrayList<List<Integer>>();
        for (int i = 0; i <= rowIndex; ++i) {
            List<Integer> row = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                if (j == 0 || j == i) {
                    row.add(1);
                } else {
                    row.add(C.get(i - 1).get(j - 1) + C.get(i - 1).get(j));
                }
            }
            C.add(row);
        }
        return C.get(rowIndex);
    }
}

优化版本代码

注意到对第 行的计算仅用到了第 行的数据，因此可以使用滚动数组的思想优化空间复杂度。

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> pre = new ArrayList<Integer>();
        for (int i = 0; i <= rowIndex; ++i) {
            List<Integer> cur = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                if (j == 0 || j == i) {
                    cur.add(1);
                } else {
                    cur.add(pre.get(j - 1) + pre.get(j));
                }
            }
            pre = cur;
        }
        return pre;
    }
}

更优版本代码

能否只用一个数组呢？
递推式 表明，当前行第 项的计算只与上一行第 项及第 项有关。

因此我们可以倒着计算当前行，这样计算到第 项时，第 项仍然是上一行的值。（不会发生覆盖）

复杂度分析

时间复杂度：

空间复杂度： 。不考虑返回值的空间占用。

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> row = new ArrayList<Integer>();
        row.add(1);
        for (int i = 1; i <= rowIndex; ++i) {
            row.add(0);
            for (int j = i; j > 0; --j) {
                row.set(j, row.get(j) + row.get(j - 1));
            }
        }
        return row;
    }
}

解题思路：线性递推

由组合数公式 ，可以得到同一行的相邻组合数的关系 ，由于，利用上述公式我们可以在线性时间计算出第 行的所有组合数。

复杂度分析

时间复杂度：

空间复杂度： 。不考虑返回值的空间占用。

我的代码

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> row = new ArrayList<Integer>();
        row.add(1);
        for (int i = 1; i <= rowIndex; ++i) {
            row.add((int) ((long) row.get(i - 1) * (rowIndex - i + 1) / i));
        }
        return row;
    }
}