[LC]238. 除自身以外数组的乘积

🚩传送门：力扣题目

题目

给你一个整数数组 ，返回 数组 ，其中 等于 中除 之外其余各元素的乘积 。

题目数据 保证 数组 之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请不要使用除法，且在 时间复杂度内完成此题。

示例 1:

输入: nums = [1,2,3,4] 输出: [24,12,8,6]

示例 2:

输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]

解题思路：左右乘积列表

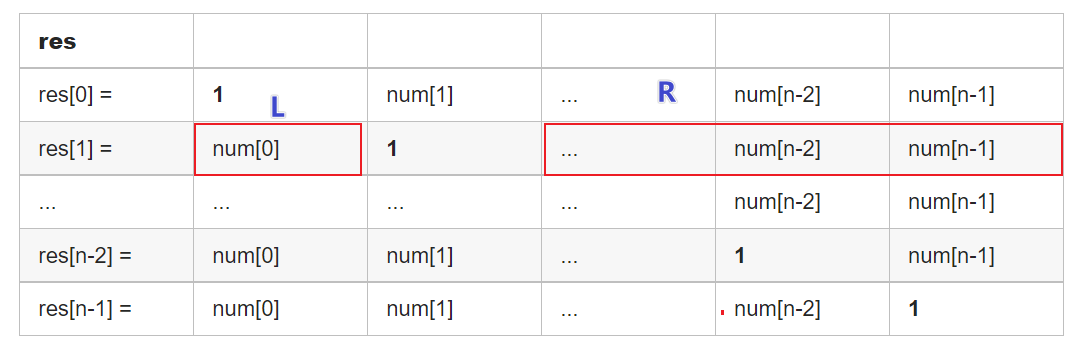
对于给定索引 ，我们将使用它左边所有数字的乘积乘以右边所有数字的乘积

复杂度分析

时间复杂度：，其中 指的是数组 的大小。

空间复杂度：，输出数组不算进空间复杂度中，因此我们只需要常数的空间存放变量。

官方代码

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int[] res = new int[nums.length];
        int L = 1, R = 1;
        // 计算 L 部分的答案
        for (int i = 0; i < nums.length; i++) {
            res[i] = L;
            L *= nums[i];
        }
        // 计算 R 部分的答案
        for (int i = nums.length - 1; i >= 0; i--) {
            res[i] *= R;
            R *= nums[i];
        }
        return res;
    }
}