[LeetCode]Dp120 三角形最小路径和 [ 漂亮在倒推 ]

传送门：https://leetcode-cn.com/problems/triangle/

题目

给定一个三角形 triangle ，找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。如(i,j) 可以移动到 (i+1,j) 或 (i+1,j+1)

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]] 输出：11 解释：如下面简图所示： 2 3 4 6 5 7 4 1 8 3

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]] 输出：-10

解题思路：动态规划 -> 降维

如果将每一行的左端对齐，那么会形成一个等腰直角三角形，如下所示：

[2]
[3,4]
[6,5,7]
[4,1,8,3]

用 dp[i][j] 表示从三角形顶部 (0,0) 走到位置 (i,j) 的最小路径和。triangle[i][j] 表示 (i,j) 元素。
这里的位置 (i, j) 指的是三角形中第 i 行第 j 列（均从 0 开始编号）的位置。

• 要想走到位置 (i,j)，上一步就只能在位置 (i-1,j) 或者位置 (i-1,j-1) ，我们在这两个位置中选择一个路径和较小的来进行转移。
• 当在 j=0 时，(i,0)只能从 (i-1,0) 过来，故 dp[i][0]=dp[i-1][0]
• 当在 j= i_jlast 时，(i,i_jlast)只能从 (i-1,i-1_jlast) 过来

因此 dp[i][j]=dp[i-1][i-1_jlast]

状态转移方程：

复杂度分析

时间复杂度：

空间复杂度：，即为存储所有状态需要的空间。

代码

下图也是为啥需要分 3 类讨论的原因，因为有 3 种类型，比较繁琐。
若用反向只有一种情况

我的代码

public class Demo {
    //动态规划,状态转移方程dp[i][j]=Min(dp[i-1][j]+nums[i][j],dp[i-1][j-1]+nums[i][j])
    public static int minimumTotal(List<List<Integer>> triangle) {
        if(triangle==null&&triangle.size()==0)return Integer.MIN_VALUE;
        if(triangle.size()==1)return triangle.get(0).get(0);
        int[][]dp=new int[triangle.size()][triangle.get(triangle.size()-1).size()];
        dp[0][0]=triangle.get(0).get(0);
        int res=Integer.MAX_VALUE;
        for (int i = 1; i < triangle.size(); i++) {
            for (int j = 0; j < triangle.get(i).size(); j++) {
                if(j==0)
                    dp[i][j]=triangle.get(i).get(j)+dp[i-1][0];
                else if(j==(triangle.get(i).size()-1))
                    dp[i][j]=triangle.get(i).get(j)+dp[i-1][j-1];
                else
                    dp[i][j]=Math.min(dp[i-1][j-1]+triangle.get(i).get(j),dp[i-1][j]+triangle.get(i).get(j));
                if(i==triangle.size()-1)
                     res=Math.min(dp[i][j],res);
            }
        }
        return res;
    }
      public static void main(String[] args) {
            List<List<Integer>>triangle=new ArrayList<List<Integer>>();
            //.....省略生成 triangle
            System.out.println(minimumTotal(triangle));
        }
}

我的优化 -> 一维数组降维

当从下向上推时，只有一种情况，不需要分类讨论，且 dp[0][0] 就是答案，一维数组下就是dp[0]

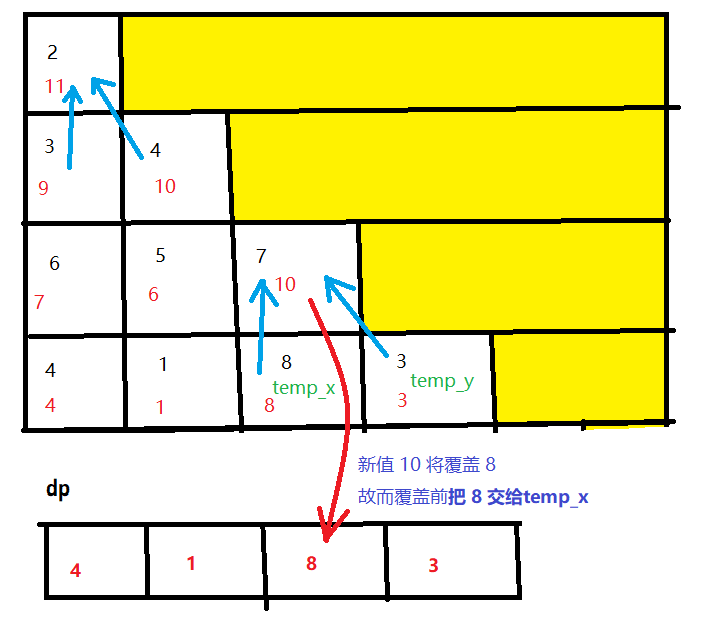
public class Demo {
    //动态规划,空间优化,必须从下向上
    public static int minimumTotal(List<List<Integer>> triangle) {
        if(triangle==null&&triangle.size()==0)return Integer.MIN_VALUE;
        if(triangle.size()==1)return triangle.get(0).get(0);
        int LENGTH=triangle.get(triangle.size()-1).size();
        int []dp=new int[LENGTH];//dp数组的长度为最后一行的元素个数
        int temp_x=0,temp_y=0;//temp_x保存会被覆盖的dp[j],temp_y保存 temp_x的右边值
        for (int i = triangle.size()-1; i >=0 ; i--) {
            if(i!=triangle.size()-1)
                temp_y=dp[triangle.get(i+1).size()-1];
            for (int j = triangle.get(i).size()-1; j >=0 ; j--) {
                if(i==triangle.size()-1) dp[j]=triangle.get(i).get(j);//dp初始化
                else{
                    temp_x=dp[j];//修改前拿出来
                    dp[j]=Math.min(dp[j]+triangle.get(i).get(j),temp_y+triangle.get(i).get(j));
                    temp_y=temp_x;
                }
            }
        }
        return dp[0];
    }
    public static void main(String[] args) {
        List<List<Integer>>triangle=new ArrayList<List<Integer>>();
        //.....省略生成 triangle
        System.out.println(minimumTotal(triangle));
    }
}

优化解释：