[LC]343. 整数拆分

🚩传送门：力扣题目

题目

给定一个正整数 ，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

示例 1:

输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

说明：你可以假设 不小于 且不大于 。

解题思路：数学推导

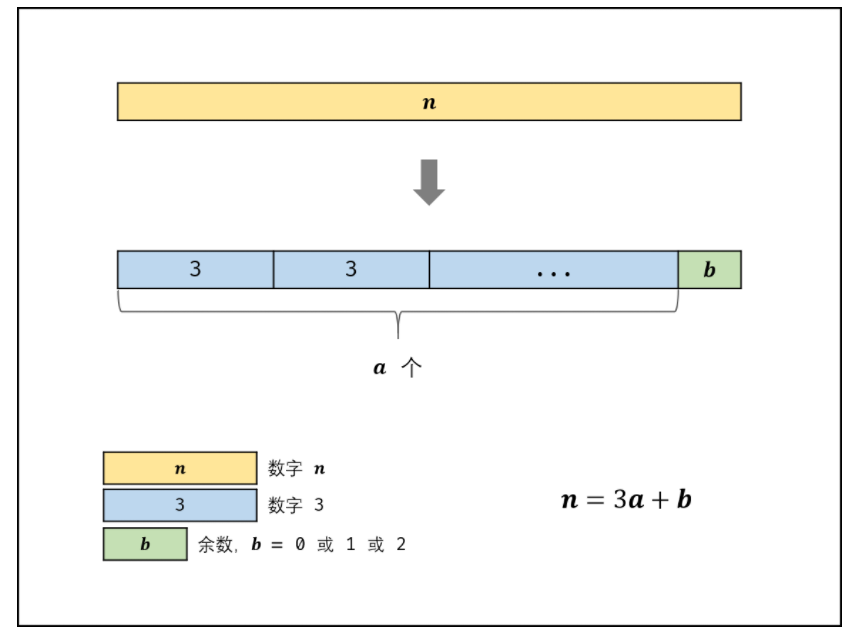
设将整数 拆分为 个小数字：

本题求解：

以下数学推导总体分为两步： ① 当所有拆分出的数字相等时，乘积最大。 ② 最优拆分数字为 3 。

数学推导

以下公式为 “算术几何均值不等式” ，等号当且仅当 时成立。

推论一：若拆分的数量 确定， 则 各拆分数字相等时，乘积最大。

推论二：将数字 尽可能以因子 等分时，乘积最大。

推论证明

  - 设将数字以因子 ![](https://cdn.nlark.com/yuque/__latex/712ecf7894348e92d8779c3ee87eeeb0.svg#card=math&code=x&id=nCmKc)_ _等分为 ![](https://cdn.nlark.com/yuque/__latex/26fdbf8e53cb0e48da5f4ddd4aaf5a5c.svg#card=math&code=a&id=bru9k) 个，即 ![](https://cdn.nlark.com/yuque/__latex/e5bce13b8aa62f0cb33754c926c7499d.svg#card=math&code=n%3Dax&id=fi2JS) [ **解释：**![](https://cdn.nlark.com/yuque/__latex/60c205404e823c5402f8506f1349fe1c.svg#card=math&code=%5Csmall%7B%5Cfrac%7Bn%7D%7Ba%7D%3Dx%7D&id=Sadcq) ] ，则乘积为 ![](https://cdn.nlark.com/yuque/__latex/b0453ceda6faa81663f03d66d0d385a6.svg#card=math&code=x%5Ea&id=EXrRW)。

由于 为常数，当 取最大值时，乘积达到最大值。

  - 根据分析，可将分体转化为求 ![](https://cdn.nlark.com/yuque/__latex/22f6ddd79568df89ddc4e176283a253c.svg#card=math&code=y%3Dx%5E%7B%5Cfrac%7B1%7D%7Bx%7D%7D&id=tx5aq) 的极大值，故而对 ![](https://cdn.nlark.com/yuque/__latex/712ecf7894348e92d8779c3ee87eeeb0.svg#card=math&code=x&id=xqcEB) 求导

取对数 (1)

对 x 求导 (2)

整理可得 (3)

  - 令 ![](https://cdn.nlark.com/yuque/__latex/85e8f65be9616c1ba437affe9d60e27f.svg#card=math&code=y%5E%7B%27%7D%3D0%20&id=Tj41F) ,则 ![](https://cdn.nlark.com/yuque/__latex/db5dfd650baa9b9b878c3f24550ad7c0.svg#card=math&code=1-ln%20x%3D0&id=hS7bN) ，易得驻点 ![](https://cdn.nlark.com/yuque/__latex/17b49eda5cf9450d8ed5169946d57a4b.svg#card=math&code=x_0%3De%20%5Capprox%202.7&id=ZZCdw) ，可知 ![](https://cdn.nlark.com/yuque/__latex/85dc97ce1d819eacb00f66dbe120b56f.svg#card=math&code=x_0%20&id=y7IBh) 处取得极大值 。
  - 由于 ![](https://cdn.nlark.com/yuque/__latex/085d987d07cedb28f45177a783c7a3bc.svg#card=math&code=x%20&id=mZJUi) 必须为整数，最接近 ![](https://cdn.nlark.com/yuque/__latex/c9a277d40d3a0b3afb85cdb557908945.svg#card=math&code=e&id=UEc0u) 的整数为 `2` 或者 `3` 。代入发现 `x=3` 时乘积最大。

拆分规则

1. 最优： 。把数字 可能拆为多个因子，余数可能为 三种情况 。
2. 次优： 。若余数为 ；则保留，不再拆为 。
3. 最差： 。若余数为 ；则应把一份 替换为 ，因为 。

备注：[ 我们希望全拆成 3 ，但是显然不可能全都符合 ]

我们能证明当 取最大值，但是我们如何保证在不完全取 的情况下余数 的正解性呢 ？

1. 首先余数为 ，说明全是 。 [ 正解 ]
2. 其次余数为 ，说明全是 一个 。
   • 全取 部分一定是最大的 。剩余的 部分也是最大的 。
   • 本身 ， 必须是整数，一定在 处取极大。 [ 正解 ]
3. 最后余数为 ，说明全是 一个 。
   • 将其拆成 个 ，一个 ，一个 ， 部分一定最大。
   • 和部分，拆成更大 [ 正解 ]

算法流程

1. 当 时，按照规则应不拆分，但题目要求必须拆分，因此拆出因子，即返回 。

2. 当 时，求 除以 的 整数部分和 余数部分 （即 ），并分类讨论

   • 当 时，直接返回 ；
   • 当 时，要将一个 转换为 ,因此返回

   • 当 时，返回

      ![image.png](https://cdn.nlark.com/yuque/0/2021/png/2955945/1618842120946-098c3071-aefa-4ed8-8e46-f85d17920c0e.png#clientId=u3759d510-ff12-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=481&id=uaec17008&margin=%5Bobject%20Object%5D&name=image.png&originHeight=641&originWidth=854&originalType=binary&ratio=1&rotation=0&showTitle=false&size=44080&status=done&style=none&taskId=u866b2c7f-d7d1-4a02-aaad-cdae8872145&title=&width=641)

复杂度分析

时间复杂度：，仅有求证、求余、次方运算 。

空间复杂度：， 和 使用常数大小额外空间 。

官方代码

class Solution {
    public int integerBreak(int n) {
        if (n <= 3) return n - 1;
        int a = n / 3, b = n % 3;
        if (b == 0) return (int) Math.pow(3, a);
        if (b == 1) return (int) Math.pow(3, a - 1) * 4;
        return (int) Math.pow(3, a) * 2;
    }
}