排序算法

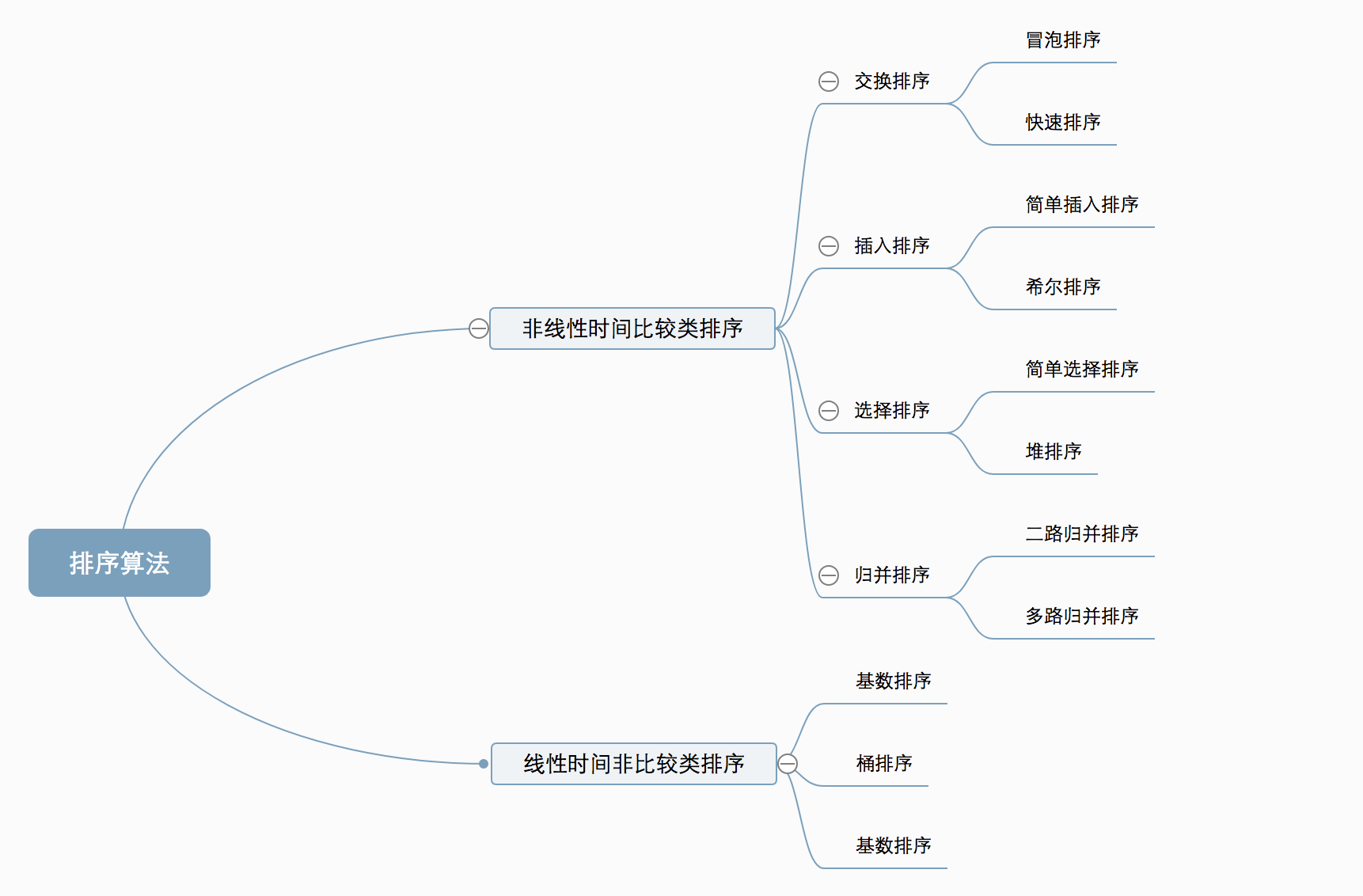
选择排序

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int len = nums.size();
        for(int i=0;i<len-1;i++){
            int k = i;
            for(int j=i+1;j<len;j++){
                if(nums[j]<nums[k]){
                    k = j;
                }
            }
            if(k!=i){
                swap(nums[i],nums[k]);
            }
        }
        return nums;
    }
};

冒泡排序

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int len = nums.size();
        for(int i=0;i<len-1;i++){
            for(int j=0;j<len-i-1;j++){
                if(nums[j]>nums[j+1]){
                    swap(nums[j],nums[j+1]);
                }
            }
        }
        return nums;
    }
};

• 时间复杂度 O(n^2)

• 空间复杂度 O(1)

  快速排序

  class Solution {
  public:
    vector<int> sortArray(vector<int>& nums) {
        q_sort(nums,0,nums.size()-1);
        return nums;
    }
    void q_sort(vector<int>& nums,int low, int high){
        if(low<high){
            int part = partation(nums,low,high);
            q_sort(nums,low,part-1);
            q_sort(nums,part+1,high);
        }
    }
    int partation(vector<int>&nums, int low,int high){
        int pivot = nums[low];
        int i=low,j=high;
        while(i<j){
            while(i<j&&nums[j]>=pivot) j--;
            nums[i] = nums[j];
            while(i<j&&nums[i]<=pivot) i++;
            nums[j] = nums[i];
        }
        nums[i] = pivot;
        return i;
    }
  };
  

• 时间复杂度 O(n^2)

• 空间复杂度 O(1)

  堆排序

  堆排序的思想就是先将待排序的序列建成大根堆，使得每个父节点的元素大于等于它的子节点。此时整个序列最大值即为堆顶元素，我们将其与末尾元素交换，使末尾元素为最大值，然后再调整堆顶元素使得剩下的 n-1 个元素仍为大根堆，再重复执行以上操作我们即能得到一个有序的序列。

如下两个动图展示了对 [4, 6, 8, 5, 9] 这个数组堆排序的过程：

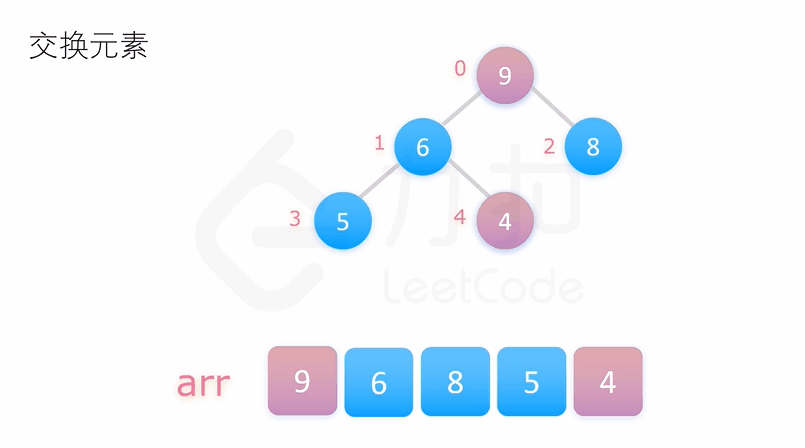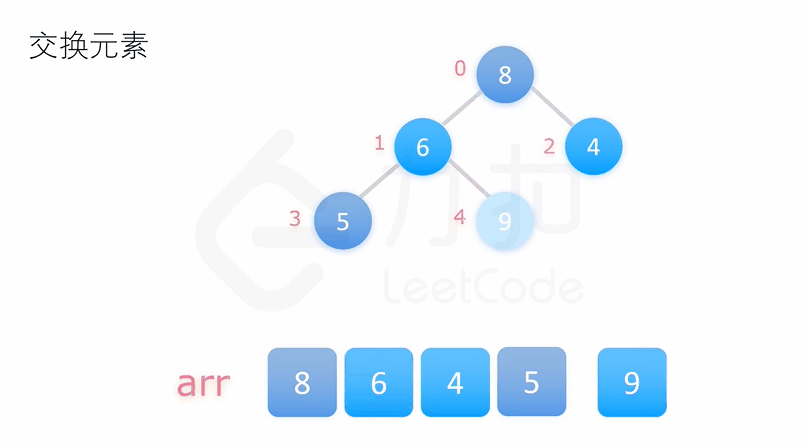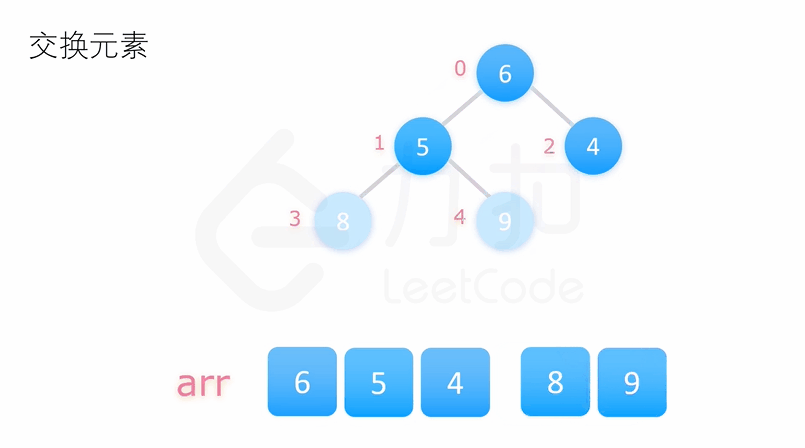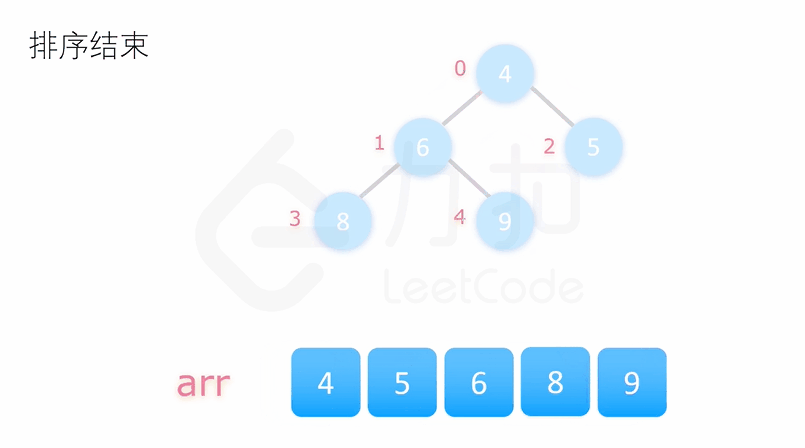
class Solution {
    void maxHeapify(vector<int>& nums, int i, int len) {
        for (; (i << 1) + 1 <= len;) {
            int lson = (i << 1) + 1;
            int rson = (i << 1) + 2;
            int large;
            if (lson <= len && nums[lson] > nums[i]) {
                large = lson;
            } else {
                large = i;
            }
            if (rson <= len && nums[rson] > nums[large]) {
                large = rson;
            }
            if (large != i) {
                swap(nums[i], nums[large]);
                i = large;
            } else {
                break;
            }
        }
    }
    void buildMaxHeap(vector<int>& nums, int len) {
        for (int i = len / 2; i >= 0; --i) {
            maxHeapify(nums, i, len);
        }
    }
    void heapSort(vector<int>& nums) {
        int len = (int)nums.size() - 1;
        buildMaxHeap(nums, len);
        for (int i = len; i >= 1; --i) {
            swap(nums[i], nums[0]);
            len -= 1;
            maxHeapify(nums, 0, len);
        }
    }
public:
    vector<int> sortArray(vector<int>& nums) {
        heapSort(nums);
        return nums;
    }
};

归并排序

class Solution {
    vector<int> tmp;
    void mergeSort(vector<int>& nums, int l, int r) {
        if (l >= r) return;
        int mid = (l + r) >> 1;
        mergeSort(nums, l, mid);
        mergeSort(nums, mid + 1, r);
        int i = l, j = mid + 1;
        int cnt = 0;
        while (i <= mid && j <= r) {
            if (nums[i] <= nums[j]) {
                tmp[cnt++] = nums[i++];
            }
            else {
                tmp[cnt++] = nums[j++];
            }
        }
        while (i <= mid) {
            tmp[cnt++] = nums[i++];
        }
        while (j <= r) {
            tmp[cnt++] = nums[j++];
        }
        for (int i = 0; i < r - l + 1; ++i) {
            nums[i + l] = tmp[i];
        }
    }
public:
    vector<int> sortArray(vector<int>& nums) {
        tmp.resize((int)nums.size(), 0);
        mergeSort(nums, 0, (int)nums.size() - 1);
        return nums;
    }
};