题目链接

牛客网
LeetCode

题目描述

给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent，求 base 的 exponent 次方。

解题思路

快速幂

递归法

下面的讨论中 x 代表 base，n 代表 exponent。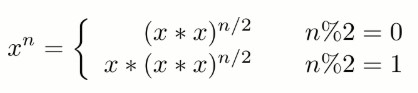
image.png
因为 (x*x)n/2 可以通过递归求解，并且每次递归 n 都减小一半，因此整个算法的时间复杂度为 O(logN)。

  1. class Solution {
  2. public:
  3.     double q_power(double b, int n)
  4.     {
  5.         if(n == 0)
  6.             return 1;
  7.         double ret  = q_power(b, n/2);
  8.         if(n % 2 ==1)
  9.             return ret * ret *b;
  10.         return ret * ret;
  11.     }
  12.     double Power(double base, int exponent) {
  13.         if(base == 0)
  14.             return 0;
  15.         if(exponent<0)//如果幂数为负
  16.         {
  17.             base = 1/base;
  18.             exponent = -exponent;
  19.         }
  20.         return q_power(base, exponent);
  21.     }
  22. };

LeetCode解法：

  1. class Solution {
  2.     public double myPow(double x, int n) {
  3.         long N = n;
  4.         if(N == 0){
  5.             return 1;
  6.         }
  7.         if(x == 0 || x == 1){
  8.             return x;
  9.         }
  10.         if(N < 0){
  11.             N = - N;
  12.             x = 1/x;
  13.         }
  14.         return Pow(x, N);
  15.     }
  16.     private double Pow(double x, long n){
  17.         if(n == 0){
  18.             return 1;
  19.         }
  20.         if(x == 0 || x == 1){
  21.             return x;
  22.         }
  23.         double res = Pow(x, n / 2);
  24.         if((n & 1) == 1){
  25.             return x * res * res;
  26.         }
  27.         return res * res;
  28.     }
  29. }
  • 时间复杂度： O(logN)。

    非递归法：

    假设求16. 数值的整数次方（快速幂） - 图2 ,已知6可以表示成二进制110可以表示成16. 数值的整数次方（快速幂） - 图3 ,所以16. 数值的整数次方（快速幂） - 图4 可以表示成16. 数值的整数次方（快速幂） - 图5 所以，对于二进制数，遇到位数是1的就乘到答案中。 ```cpp class Solution { public:
  1. double Power(double base, int exponent) {
  2.     if(exponent < 0)
  3.     {
  4.         base = 1/base;
  5.         exponent = -exponent;
  6.     }
  7.     double x = base;
  8.     double ret = 1.0;
  9.     while(exponent)
  10.     {
  11.         // exponent为奇数if判断会成立两次，第一次和最后一次
  12.         // exponent为偶数if判断会成立一次，最后一次
  13.         if(exponent&1) // 判断当前最后一位是否为1(是否为奇数)
  14.         {
  15.             ret *= x;
  16.         }
  17.         x *=x;//x不断翻倍
  18.         exponent >>=1;//右移，去掉最低位
  19.     }
  20.     return ret;
  21. }

};

/// class Solution { public: double Power(double base, int exponent) { if(exponent==0) return 1; if(exponent==1) return base; if(base==0) return 0; if(exponent<0){ exponent = -exponent; base = 1/base; } double x = base; while(exponent>1){ x = x; exponent >>=1; } if(exponent&1) return xbase; return x; } }; ``` 上述方法相当于遍历n的二进制位，是1就乘进结果（如x的6次方，x为1次,2次，4次，当exponent&1为1时，即2次，4次，乘入x的2次，4次）。

  • 时间复杂度：O(logn)，因为n的二进制位个数为logn
  • 空间复杂度：O(1)