题目链接

LeetCode

题目描述

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入： nums = [1,2,3]
输出： [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入： nums = [0,1]
输出： [[0,1],[1,0]]

示例 3：

输入： nums = [1]
输出： [[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同
解题思路
方法一：回溯法+dfs
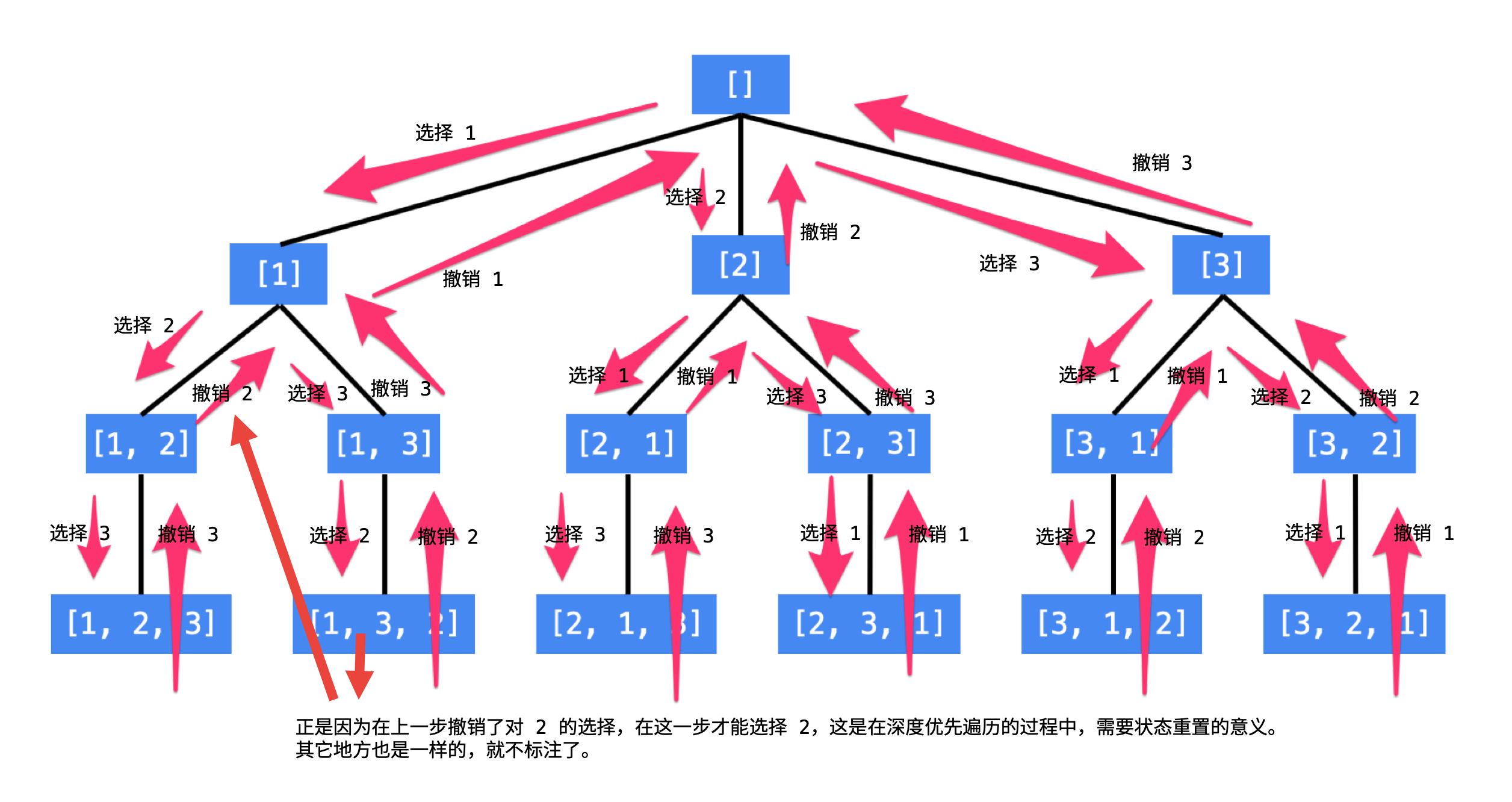
这个问题可以看作有 n 个排列成一行的空格，我们需要从左往右依此填入题目给定的 n 个数，每个数只能使用一次。那么很直接的可以想到一种穷举的算法，即从左往右每一个位置都依此尝试填入一个数，看能不能填完这 n 个空格，在程序中我们可以用「回溯法」来模拟这个过程。

我们定义递归函数 backtrack(first, output) 表示从左往右填到第 first 个位置，当前排列为 output。那么整个递归函数分为两个情况：

如果 first==n，说明我们已经填完了 n 个位置（注意下标从 0 开始），找到了一个可行的解，我们将output 放入答案数组中，递归结束。
如果 first<n，我们要考虑这第 first 个位置我们要填哪个数。根据题目要求我们肯定不能填已经填过的数，因此很容易想到的一个处理手段是我们定义一个标记数组 vis[] 来标记已经填过的数，那么在填第 first 个数的时候我们遍历题目给定的 n 个数，如果这个数没有被标记过，我们就尝试填入，并将其标记，继续尝试填下一个位置，即调用函数 backtrack(first + 1, output)。回溯的时候要撤销这一个位置填的数以及标记，并继续尝试其他没被标记过的数。

46. 全排列** - 图1

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        reback(nums,0,nums.size());
        return res;
    }
private:
    vector<vector<int>> res;
    void reback(vector<int>& path,int pos,int len){
        if(pos==len){
            res.push_back(path);
            return;
        }
        for(int i=pos;i<len;i++){
            swap(path[i],path[pos]);
            reback(path,pos+1,len);
            swap(path[i],path[pos]);
        }
    }
};

class Solution {
    List<List<Integer>> res;
    List<Integer> path;
    public List<List<Integer>> permute(int[] nums) {
        res = new LinkedList<List<Integer>>();
        path = new LinkedList<Integer>();
        backstrack(nums, 0);
        return res;
    }
    private void backstrack(int[] nums, int pos){
        if(pos == nums.length){
            res.add(new LinkedList<Integer>(path));    // 重点代码
            return;
        }
        for(int i = pos; i < nums.length; ++i){
            swap(nums, pos, i);
            path.add(nums[pos]);  // 重点代码
            backstrack(nums, pos + 1);    // 重点代码
            path.remove(path.size()-1);    // 重点代码
            swap(nums, pos, i);
        }
    }
    private void swap(int[] nums, int i, int j){
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

时间复杂度 O(n*n!)
空间复杂度 O(n)

46. 全排列**

题目链接

题目描述

解题思路

方法一：回溯法+dfs