题目链接

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：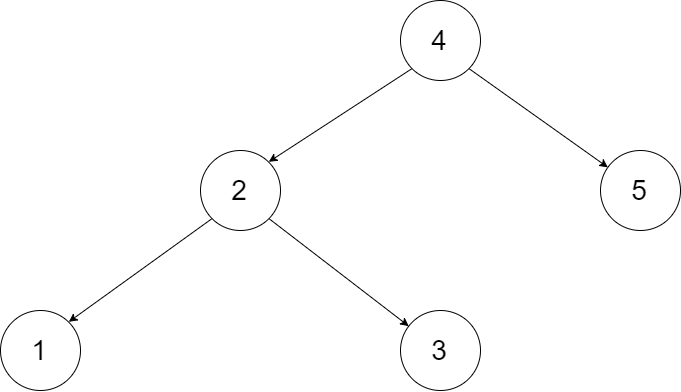
36. 二叉搜索树与双向链表** - 图1
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。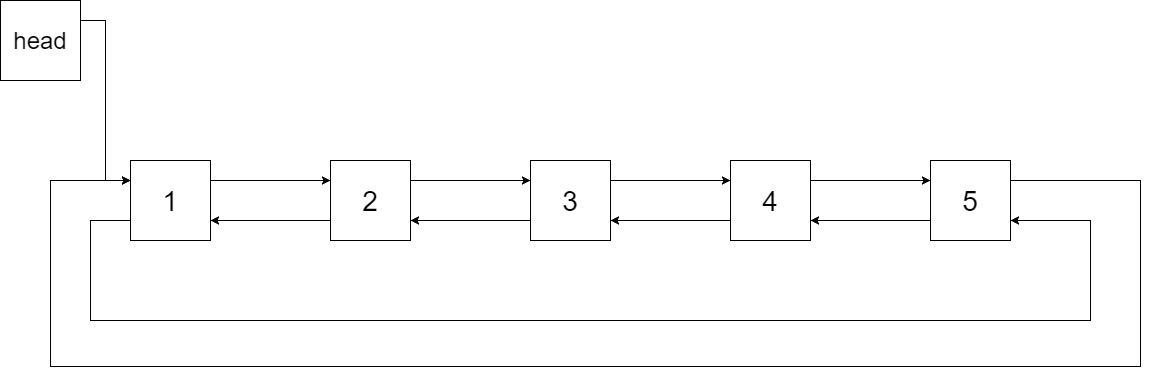
36. 二叉搜索树与双向链表** - 图2
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

解题思路

本文解法基于性质：二叉搜索树的中序遍历为 递增序列 。
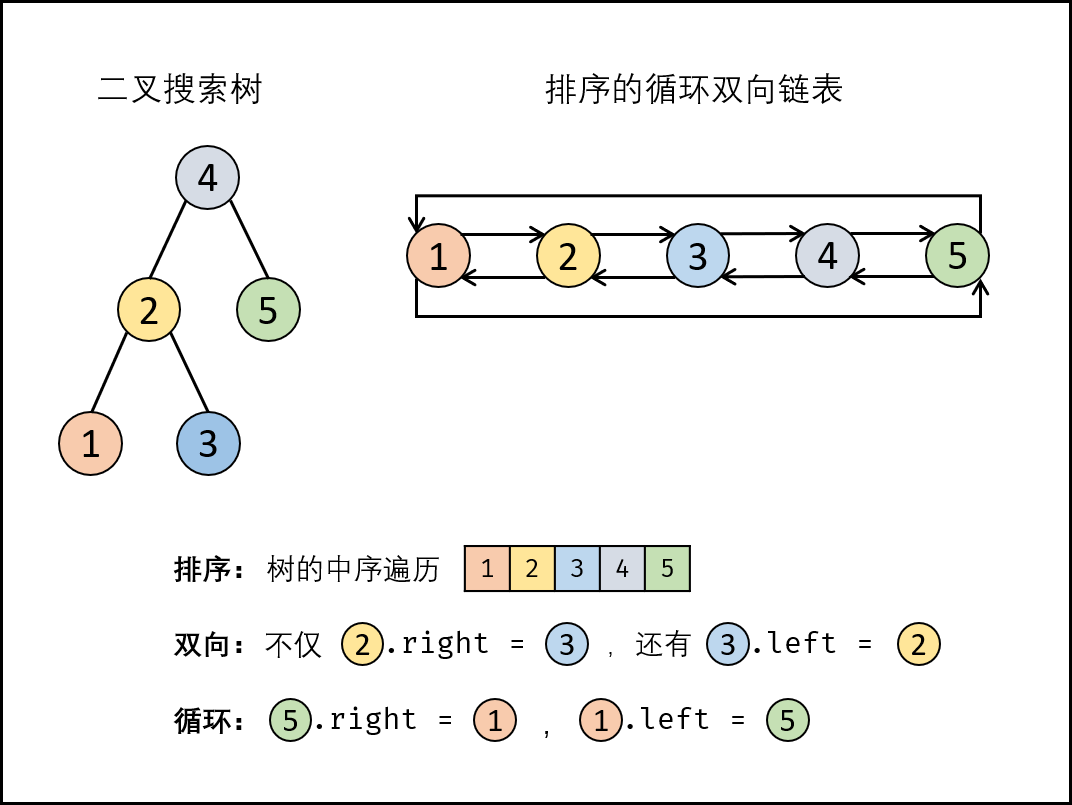
将二叉搜索树转换成一个 “排序的循环双向链表” ，其中包含三个要素：

排序链表： 节点应从小到大排序，因此应使用 中序遍历 “从小到大”访问树的节点；
双向链表： 在构建相邻节点（设前驱节点 pre ，当前节点 cur ）关系时，不仅应 pre.right=cur ，也应 cur.left = pre 。
循环链表： 设链表头节点 head 和尾节点 tail ，则应构建 head.left=tail 和 tail.right=head 。

36. 二叉搜索树与双向链表** - 图3

考虑使用中序遍历访问树的各节点 cur ；并在访问每个节点时构建 cur 和前驱节点 pre 的引用指向；中序遍历完成后，最后构建头节点和尾节点的引用指向即可。

算法流程：

**dfs(cur):** 递归法中序遍历；

终止条件： 当节点 cur 为空，代表越过叶节点，直接返回；
递归左子树，即 dfs(cur.left) ；
构建链表：
1. 当 pre 为空时： 代表正在访问链表头节点，记为 head 。
2. 当 pre 不为空时： 修改双向节点引用，即 pre.right=cur， cur.left=pre ；
3. 保存 cur ： 更新 pre=cur ，即节点 cur 是后继节点的 pre ；
递归右子树，即 dfs(cur.left) ；

**treeToDoublyList(root)：**

特例处理： 若节点 root 为空，则直接返回；
初始化： 空节点 pre ；
转化为双向链表： 调用 dfs(root) ；
构建循环链表： 中序遍历完成后，head 指向头节点， pre 指向尾节点，因此修改 head 和 pre 的双向节点引用即可。
返回值： 返回链表的头节点 head 即可。

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node() {}
    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }
    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        if(root==NULL) return NULL;
        dfs(root);
        head->left = pre;
        pre->right = head;
        return head;
    }
private:
    Node* head;
    Node* pre;
    void dfs(Node* cur){
        if(cur==NULL)
            return;
        dfs(cur->left);
        if(pre!=NULL)
            pre->right = cur;// 当 pre 不为空时： 修改双向节点引用，即 pre.right=cur， cur.left=pre ；
        else
            head = cur;// 当 pre 为空时： 代表正在访问链表头节点，记为 head 。
        cur->left = pre;
        pre = cur;// 保存 cur ： 更新 pre=cur ，即节点 cur 是后继节点的 pre ；
        dfs(cur->right);
    }
};

时间复杂度 O(N) ： N 为二叉树的节点数，中序遍历需要访问所有节点。

空间复杂度 O(N) ： 最差情况下，即树退化为链表时，递归深度达到 N，系统使用 O(N) 栈空间。

中序遍历法

/*
// Definition for a Node.
class Node {
public:
  int val;
  Node* left;
  Node* right;
  Node() {}
  Node(int _val) {
      val = _val;
      left = NULL;
      right = NULL;
  }
  Node(int _val, Node* _left, Node* _right) {
      val = _val;
      left = _left;
      right = _right;
  }
};
*/
class Solution {
public:
  Node* treeToDoublyList(Node* root) {
      if(root==NULL)
          return NULL;
     dfs(root);
     Node *head = new Node();
     Node *cur = new Node(res[0]);
     head->right = cur;
     Node *first = cur;
      for(int i=1;i<res.size();i++){
          Node *tmp = new Node(res[i]);
          cur->right = tmp;
          tmp->left = cur;
          cur = tmp;
      }
      cur->right = first;
      first->left = cur; 
      return first;
  }
private:
  vector<int> res;
  // 中序遍历
  void dfs(Node* root){
      if(root==NULL)
          return;
      dfs(root->left);
      res.push_back(root->val);
      dfs(root->right);
  }
};