题目链接

牛客网
LeetCode

题目描述

请实现一个函数用来匹配包括 ‘.’ 和 ‘‘的正则表达式。模式中的字符’.’表示任意一个字符，而’‘ 表示它前面的字符可以出现任意次（包含 0 次）。

在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串 “aaa” 与模式 “a.a” 和 “abaca”匹配，但是与”aa.a”和”ab*a” 均不匹配。

示例1

输入
"aaa","a*a"
返回值
true

解题思路

方法一：递归

假设主串为s，长度为sn， 模式串为p，长度为pn，对于模式串p当前的第i位来说，有'正常字符'、'*'、'.'三种情况。我们针对这三种情况进行讨论：

1. 如果p[i]为正常字符， 那么我们看s[i]是否等于p[i], 如果相等，说明第i位匹配成功,接下来看s[i+1...sn-1] 和 p[i+1...pn-1]
2. 如果p[i] 为'.', 它能匹配任意字符，直接看s[i+1...sn-1] 和 p[i+1...pn-1]
3. 如果p[i]为'*'， 表明p[i-1]可以重复0次或者多次，需要把p[i-1] 和 p[i]看成一个整体.
   • 如果p[i-1]重复0次，则直接看s[i...sn-1] 和 p[i+2...pn-1]
   • 如果p[i-1]重复一次或者多次,则直接看s[i+1...sn-1] 和p[i...pn-1]，但是有个前提：s[i]==p[i] 或者 p[i] == '.'

三种情况如下图：




显然上述的过程可以递归进行计算。
则递归三部曲为：

1. 递归函数功能：match(s, p) -> bool, 表示p是否可以匹配s
2. 递归终止条件：
   • 如果s 和 p 同时为空，表明正确匹配
   • 如果s不为空，p为空，表明，不能正确匹配
   • 如果s为空，p不为空，需要计算，不能直接给出结果
3. 下一步递归：
   • 对于前面讨论的情况1，2进行合并，如果*s == *p || *p == '.',则match(s+1, p+1)
   • 对于情况3，如果重复一次或者多次，则match(s+1,p),如果重复0次，则match(s, p+2)

具体代码如下：

class Solution {
public:
    bool match(char* s, char* p)
    {    // 如果 s 和 p 同时为空
        if (*s == '\0' && *p == '\0') return true;
        // 如果 s不为空， 但是 p 为空
        if (*p == '\0') return false;
        // 如果没有 '*'
        if (*(p+1) != '*') {
            if (*s != '\0' && (*s == *p || *p == '.'))
                return match(s+1, p+1);
            else
                return false;
        }
        // 如果有 '*'
        else {
            bool ret = false;
            // 重复 1 次或多次
            if (*s != '\0' && (*s == *p || *p == '.'))
                ret = match(s+1, p);
            // 重复 0 次
            return ret || match(s, p+2);
        }
    }
};

class Solution {
    private int slen, plen;
    public boolean isMatch(String s, String p) {
        this.slen = s.length();
        this.plen = p.length();
        return recur(s, p, 0, 0);
    }
    private boolean recur(String s, String p, int i, int j){
        // 两个字符串都为空，匹配成功，返回true
        if(i == slen && j == plen){
            return true;
        }
        // 正则表达式已经匹配完，但是字符串还没匹配完，匹配失败，返回false
        if(j == plen){
            return false;
        }
        // 正则表达式下一个字符为 '*'，说明当前字符可能重复0-n次
        if(j+1 < plen && p.charAt(j+1) == '*' ){
            boolean res = false;
            // 重复 1-n 次的结果，当前的字符串和正则表达式匹配
            if(i < slen && (s.charAt(i) == p.charAt(j) ||(p.charAt(j) == '.'))){
                res = recur(s, p, i+1, j);
            }
            // recur(s, p, i, j+2)表示当前字符重复0次的结果
            return res || recur(s, p, i, j+2);
        // 当前字符不重复
        }else{
            if(i < slen && s.charAt(i) == p.charAt(j)|| p.charAt(j) == '.'){
                return recur(s, p, i+1,j+1);
            }else{
                return false;
            }
        }
    }
}

方法二：动态规划

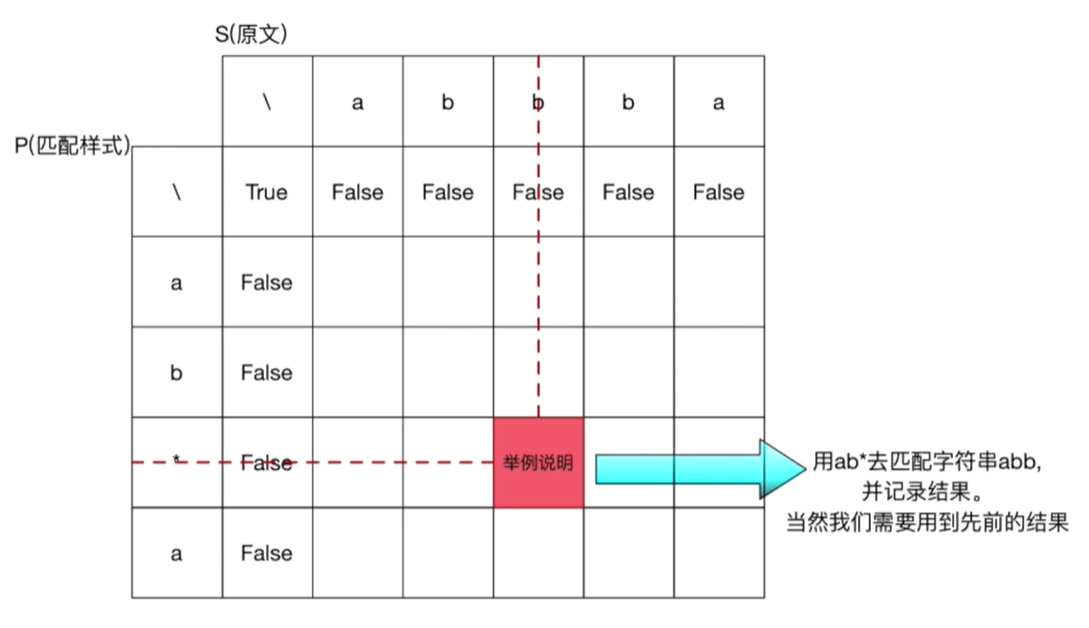
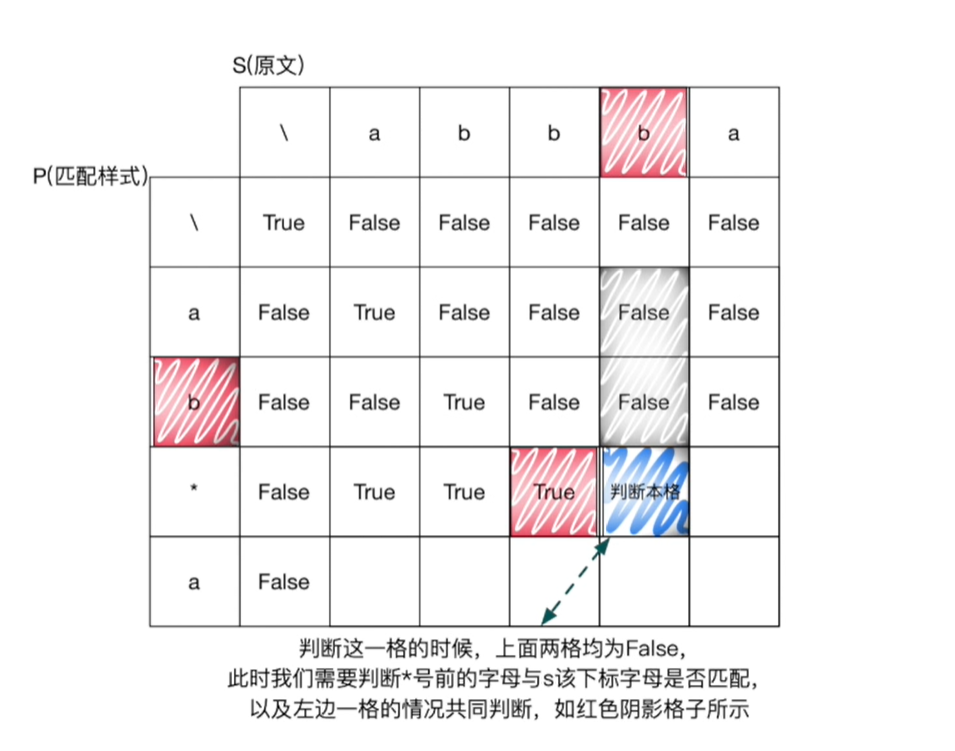
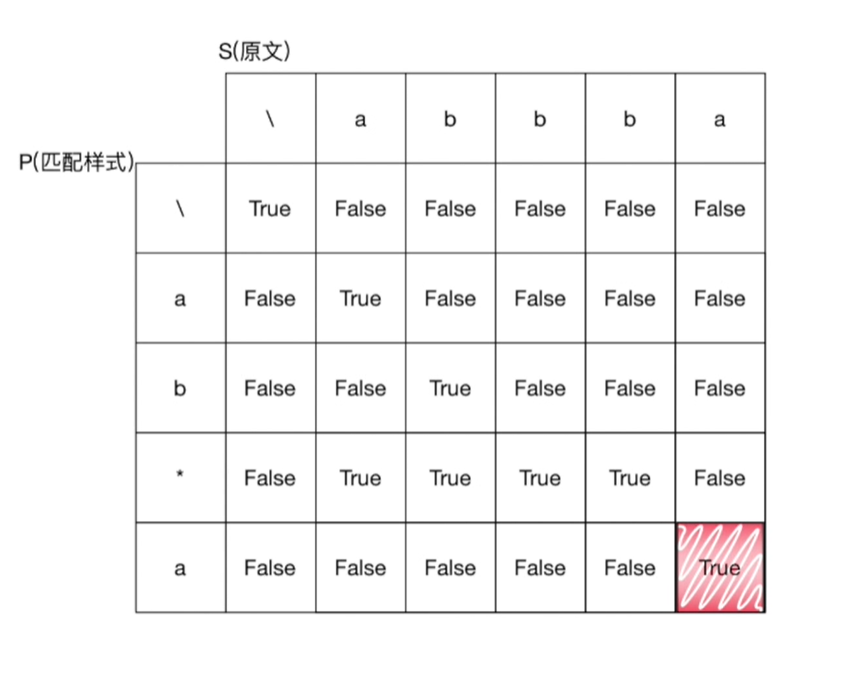
方法一的递归代码属于自顶向下，而动态规划的代码属于自底向上。

1. 动态规划转移方程：
   f[i][j]表示s的前i个和p的前j个能否匹配

• 对于方法一种的1,2两种情况可知：f[i][j] = f[i-1][j-1]
• 对于第3种情况可知：
  • 如果重复0次，f[i][j] = f[i][j-2]
  • 如果重复1次或者多次，f[i][j] = f[i-1][j]

1. 动态规划初始条件：

• s为空且p为空，为真: f[0][0] = 1
• s不为空且p为空,为假: f[1..sn][0] = 0

代码如下：

class Solution {
public:
    bool match(char* s, char* p)
    {
        int sn = strlen(s), pn = strlen(p);
        vector<vector<char>> f(sn+1, vector<char>(pn+1, 0));
        for (int i=0; i<=sn; ++i) {
            for (int j=0; j<=pn; ++j) {
                // 初始条件
                if (j == 0) 
                    f[i][j] = (i == 0);
                else {
                    // 如果没有 '*'
                    if (p[j-1] != '*') {
                        if (i >= 1 && (s[i-1] == p[j-1] || p[j-1] == '.')) {
                            f[i][j] = f[i-1][j-1];
                        }
                    }
                    // 如果有 '*'
                    else {
                        // 重复 0 次
                        if (j >= 2) {
                            f[i][j] = f[i][j-2];
                        }
                        // 重复 1 次或者多次
                        // 这里要用 | 连接， 不然重复 0 次的会直接覆盖
                        if (i >= 1 && j>=2 && (s[i-1] == p[j-2] || p[j-2] == '.')) {
                            f[i][j] = f[i][j] | f[i-1][j];
                        }
                    }
                }

            }
        }
        return f[sn][pn];
    }
};

class Solution {
    public boolean isMatch(String s, String p) {
        int slen = s.length();
        int plen = p.length();
        // dp[i][j]表示s的前i个和p的前j个能否匹配
        // 下标为字符串长度为0 - slen  0- plen之间
        // 默认所有为false
        boolean[][] dp = new boolean[slen+1][plen+1];
        for(int i = 0; i <= slen; ++i){
            for(int j = 0; j <= plen; ++j){
                // 当正则表达式长度为0时,只有 字符串也为0为true;
                if(j == 0){
                    dp[i][j] = (i == 0);
                }else{
                    // 正则表达式第 j 个字符为 '*'
                    if(p.charAt(j-1) == '*'){
                        // 正则表达式长度大于等于 2
                        if(j >= 2){
                            dp[i][j] = dp[i][j-2];  // '*' 前字符重复0次的结果
                        }
                        // '*' 前字符重复 n 次的结果
                        if(i >= 1 && j >= 2 && (s.charAt(i-1) == p.charAt(j-2) || p.charAt(j-2) == '.')){
                            dp[i][j] = dp[i][j] || dp[i-1][j]; // 两种可能取与
                        }
                    // // 正则表达式第 j 个字符不为 '*'
                    }else{
                        // 当前字符匹配成功
                        if(i >= 1 && (s.charAt(i-1) == p.charAt(j-1) || p.charAt(j-1) == '.')){
                            dp[i][j] = dp[i-1][j-1];
                        }
                    }
                }
            }
        }
        return dp[slen][plen];

    }
}

• 时间复杂度：O(mn)，其中 m 和 n 分别是字符串 s 和 p 的长度。我们需要计算出所有的状态，并且每个状态在进行转移时的时间复杂度为 O(1)。
• 空间复杂度：O(mn)，即为存储所有状态使用的空间。