题目链接

LeetCode

题目描述

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数即 999。

解题思路

方法一：暴力法

暴力遍历所有数

  1. class Solution {
  2. public:
  3.     vector<int> printNumbers(int n) {
  4.         if(n<1)
  5.             return {};
  6.         int index = 1;
  7.         for(int i=0;i<n;i++)
  8.             index *=10;
  9.         vector<int> res;
  10.         for(int i=1;i<index;i++)
  11.             res.push_back(i);
  12.         return res;
  13.     }
  14. };
  • 时间复杂度 O(10^n) ： 生成长度为 10^n 的列表需使用 O(10^n)时间。
  • 空间复杂度 O(1) ： 建立列表需使用 O(1) 大小的额外空间（ 列表作为返回结果，不计入额外空间 ）。

方法二：用字符串模拟数字加法。

  1. class Solution {
  2. public:
  3.     vector<int> output;
  4.     vector<int> printNumbers(int n) {
  5.         // 以下注释的前提：假设 n = 3
  6.         if(n <= 0) return vector<int>(0);
  7.         string s(n, '0'); // s最大会等于999，即s的长度为n
  8.         while(!overflow(s)) 
  9.             inputNumbers(s);
  10.         return output;
  11.     }
  12.     bool overflow(string& s)
  13.     {
  14.         // 本函数用于模拟数字的累加过程，并判断是否越界（即 999 + 1 = 1000，就是越界情况）
  15.         bool isOverFlow = false;
  16.         int carry = 0; // carry表示进位
  17.         for(int i=s.length()-1; i>=0; --i)
  18.         {
  19.             int current = s[i] - '0' + carry; // current表示当前这次的操作
  20.             if(i == s.length() - 1) current ++; // 如果i此时在个位，current执行 +1 操作
  21.             if(current >= 10)
  22.             {
  23.                 // 假如i已经在最大的那一位了，而current++之后>=10，说明循环到头了，即999 + 1 = 1000
  24.                 if(i == 0) isOverFlow = true;
  25.                 else
  26.                 {
  27.                     // 只是普通进位，比如current从9变成10
  28.                     carry = 1;
  29.                     s[i] = current - 10 + '0'; 
  30.                 }
  31.             }
  32.             else
  33.             {
  34.                 // 如果没有进位，更新s[i]的值，然后直接跳出循环，这样就可以回去执行inputNumbers函数了，即往output里添加元素
  35.                 s[i] = current + '0';
  36.                 break;
  37.             }
  38.         }
  39.         return isOverFlow;
  40.     }
  41.     void inputNumbers(string s)
  42.     {
  43.         // 本函数用于循环往output中添加符合传统阅读习惯的元素。比如001，我们会添加1而不是001。
  44.         bool isUnwantedZero = true; // 判断是否是不需要添加的0，比如001前面的两个0
  45.         string temp = "";
  46.         for(int i=0; i<s.length(); ++i)
  47.         {
  48.             if(isUnwantedZero && s[i] != '0') isUnwantedZero = false;
  49.             if(!isUnwantedZero) temp += s[i];
  50.         }
  51.         output.push_back(stoi(temp));
  52.     }
  53. };
  • 时间复杂度 O(10^n)

    方法三：递归+回溯(考虑到大数问题)

    由于 n 可能会非常大，因此不能直接用 int 表示数字，而是用 char 数组进行存储。
    使用回溯法得到所有的数。

1. 表示大数的变量类型：

  • 无论是 short / int / long … 任意变量类型，数字的取值范围都是有限的。因此，大数的表示应用字符串 String 类型。

    2. 生成数字的字符串集：

  • 使用 int 类型时，每轮可通过 +1 生成下个数字，而此方法无法应用至 String 类型。并且， String 类型的数字的进位操作效率较低，例如 “9999” 至 “10000” 需要从个位到千位循环判断，进位 4 次。

  • 观察可知，生成的列表实际上是 n 位 0 - 9 的 全排列 ，因此可避开进位操作，通过递归生成数字的 String 列表。

    3. 递归生成全排列：

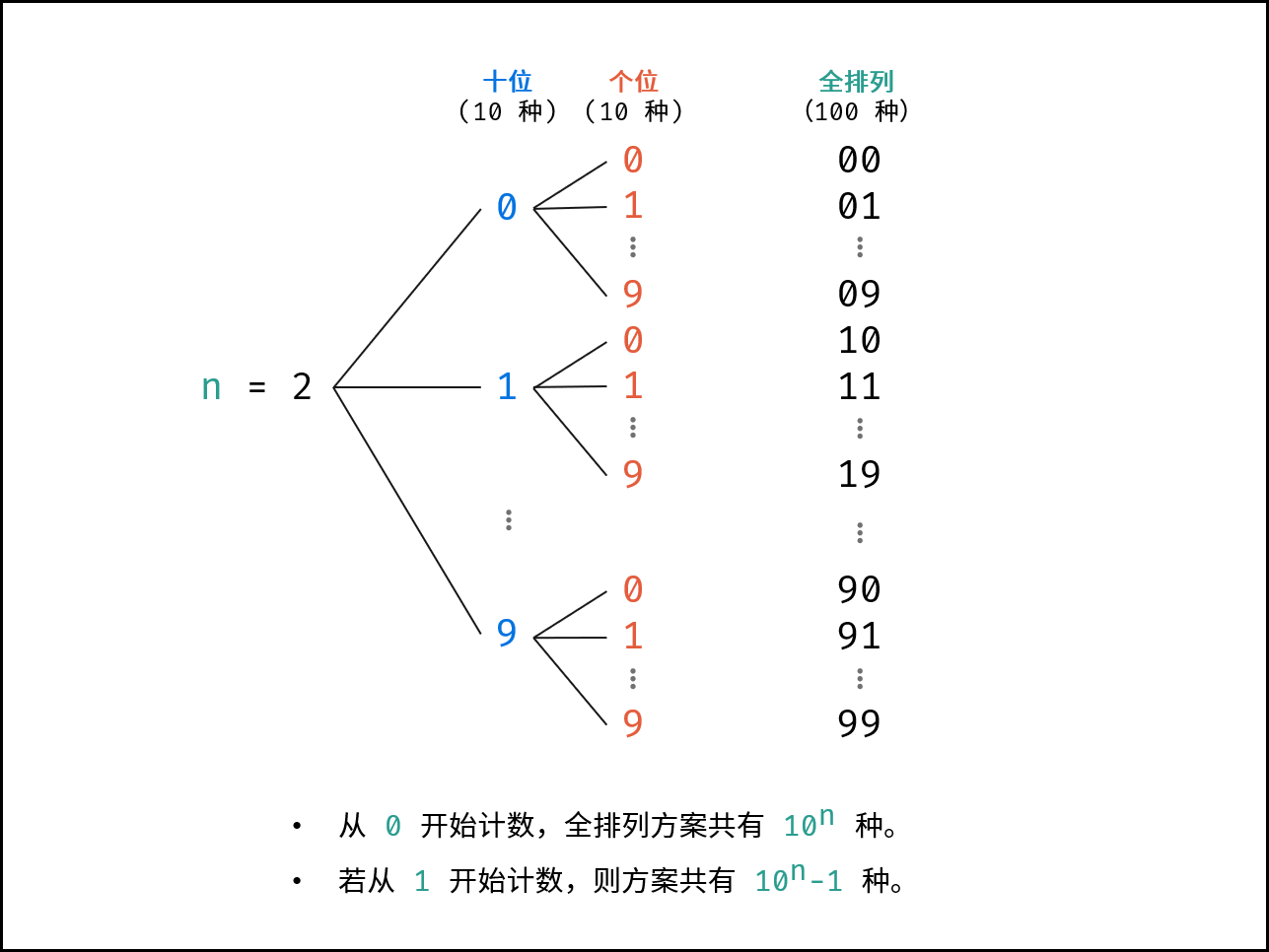
  • 基于分治算法的思想，先固定高位，向低位递归，当个位已被固定时，添加数字的字符串。例如当 n = 2 时（数字范围 1 - 9 ），固定十位为 0 - 9 ，按顺序依次开启递归，固定个位 0 - 9 ，终止递归并添加数字字符串。

17. 打印从 1 到最大的 n 位数 - 图1

class Solution {
public:
    vector<int> output;
    vector<int> printNumbers(int n) {
        if(n <= 0) return vector<int>(0);
        string s(n, '0');
        for(int i=0; i<=9; ++i)
        {
            s[0] = i + '0';
            permutation(s, s.length(), 1);
        }
        return output;
    }
    void permutation(string& s, int length, int pos)
    {
        // 这个函数的执行机制我想了好久才弄明白，mark一下，对带有循环的递归有时候还挺绕的
        if(pos == length)
        {
           inputNumbers(s);
           return; 
        }
        for(int i=0; i<=9; ++i)
        {
            s[pos] = i + '0';
            permutation(s, length, pos + 1);
        }
    }
    void inputNumbers(string s)
    {
        // 本函数与方法二的同名函数基本一样
        bool isUnwantedZero = true;
        string temp = "";
        for(int i=0; i<s.length(); ++i)
        {
            if(isUnwantedZero && s[i] != '0') isUnwantedZero = false;
            if(!isUnwantedZero) temp += s[i];
        }
        if(temp != "") 
            output.push_back(stoi(temp)); // 如果 s = "000"，则temp会是空，stoi无法执行，会报错
    }
};
  • 时间复杂度 O(10^n)
  • 空间复杂度 O(10^n)