题目链接

LeetCode

题目描述

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

示例 1:

输入: num1 = “2”, num2 = “3”
输出: “6”

示例 2:

输入: num1 = “123”, num2 = “456”
输出: “56088”

说明：

1. num1 和 num2 的长度小于 110。
2. num1 和 num2 只包含数字 0-9。
3. num1 和 num2 均不以零开头，除非是数字 0 本身。
4. 不能使用任何标准库的大数类型（比如 BigInteger）或直接将输入转换为整数来处理。

   解题思路

   方法一：模拟竖式乘法

   

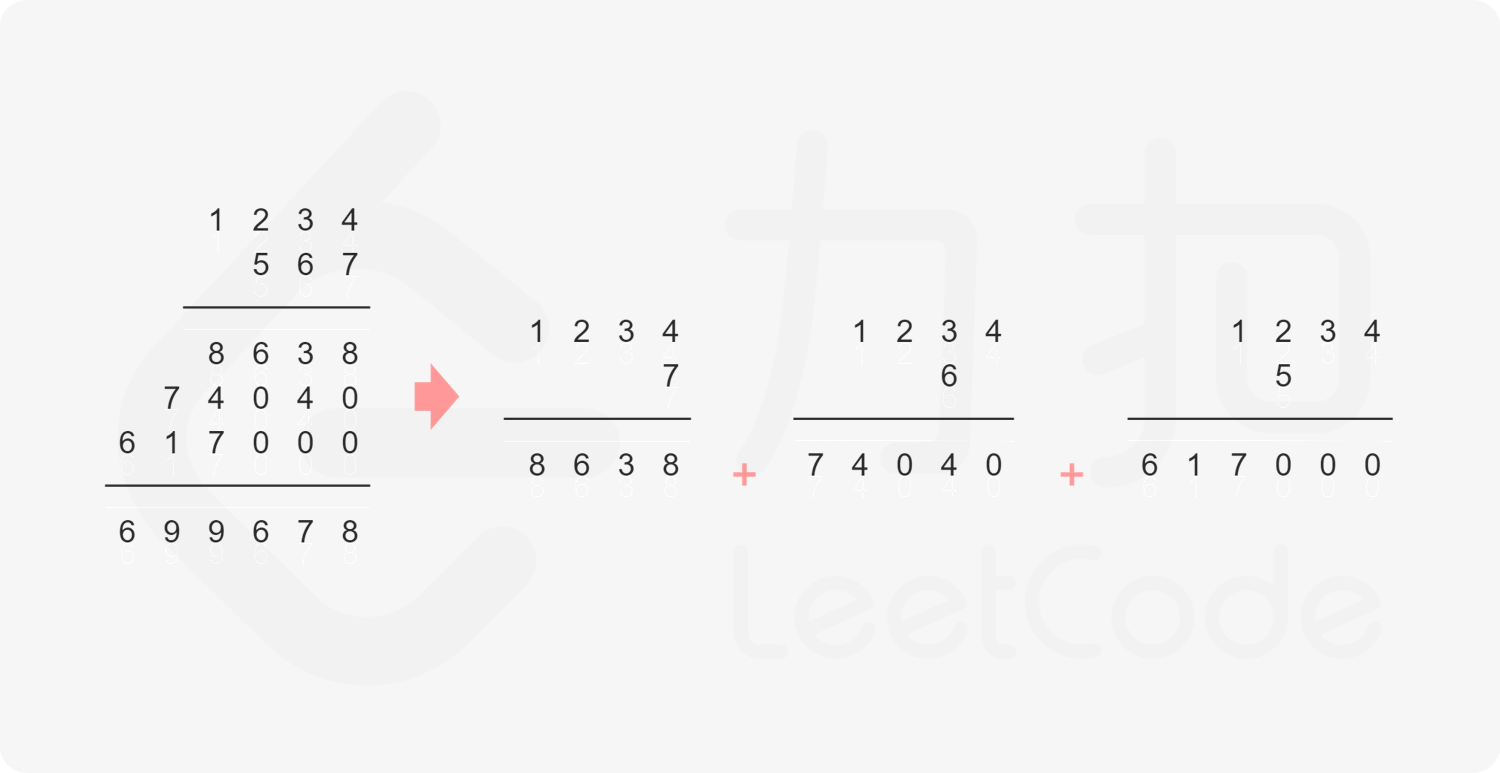
   class Solution {
    public String multiply(String num1, String num2) {
        // 特殊情况，某个数为0
        if(num1.equals("0")||num2.equals("0")){
            return "0";
        }
        String tmp;
        String res = "";
        // num2从高位到低位，先乘结果*10加后面的结果
        for(int i = 0;i<num2.length();++i){
            // 当前位和num1相乘
            tmp = multi(num1, num2.charAt(i));
            // 加上之前的结果
            res = add(res,tmp);
        }
        return res;
    }
    // 字符串乘法
    private String multi(String s,char c){
        StringBuilder sb = new StringBuilder();
        int tmp;
        int x = 0;
        for(int i = s.length()-1;i>=0;--i){
            tmp = (s.charAt(i)-'0')*(c-'0') + x;
            sb.append(tmp%10);
            x = tmp/10;
        }
        if(x!=0){
            sb.append(x);
        }
        return sb.reverse().toString();
    }
    // 字符串加法
    private String add(String s,String c){
        StringBuilder sb = new StringBuilder();
        // 先把c的最后一位加上，相当于s*10,个位结果是0+c[c.length()-1]
        sb.append(c.charAt(c.length()-1));
        int tmp;
        int x = 0;
        int i = s.length()-1,j = c.length()-2;
        while(i>=0||j>=0){
            int x1 = i>=0? s.charAt(i--) - '0':0;
            int x2 = j>=0? c.charAt(j--) - '0':0;
            tmp = x1 + x2 + x;
            sb.append(tmp%10);
            x = tmp/10;
        }
        if(x!=0){
            sb.append(x);
        }
        return sb.reverse().toString();
    }

• 时间复杂度 O(mn + n^2) m和n分别是num1和num2的长度
• 空间复杂度 O(m + n)

  方法二：乘法 数组保存

class Solution {
    public String multiply(String num1, String num2) {
        // 特殊情况，某个数为0
        if(num1.equals("0")||num2.equals("0")){
            return "0";
        }
        int m = num1.length(),n = num2.length();
        // 两个数相乘 结果长度最大为m+n最小为m+n-1
        int[] res = new int[m+n];
        for(int i = m - 1;i>=0;--i){
            // num1中第i位数和num2中所有数相乘
            int x = num1.charAt(i) - '0';
            for(int j = n-1;j>=0;--j){
                int y = num2.charAt(j) - '0';
                // 结果加入相应的位置
                // 第一个数对应m+n-1的位置 以此向前移动
                res[i+j+1] += x * y;
            }
        }
        // 将各个位置的数分配，使之成为10进制
        for(int i = m+n-1;i>0;--i){
            res[i-1] += res[i]/10;
            res[i] %= 10;
        }
        // 如果第一位为0 则从第二位开始遍历字符串
        int index = res[0] == 0? 1:0;
        StringBuilder sb = new StringBuilder();
        while(index<m+n){
            sb.append(res[index++]);
        }
        return sb.toString();
    }
}

class Solution {
    public String multiply(String num1, String num2) {
        if(num1.length() == 0 || num2.length() == 0){
            return "0";
        }
        char[] arr1 = num1.toCharArray();
        char[] arr2 = num2.toCharArray();
        if(arr1[0] == '0' || arr2[0] == '0'){
            return "0";
        }
        int[] res = new int[arr1.length + arr2.length];
        // 竖式乘法
        for(int x = arr1.length - 1; x >= 0; --x){
            int i = arr1[x] - '0';
            for(int y = arr2.length - 1; y >= 0; --y){
                int j = arr2[y] - '0';
                res[x + y] += (res[x + y + 1] + i * j)/10;
                res[x + y + 1] = (res[x + y + 1] + i * j)%10;
            }
        }
        StringBuilder sb = new StringBuilder();
        int pos = 0;
        if(res[0] == 0){
            ++pos;
        }
        while(pos < res.length){
            sb.append(res[pos++]);
        }
        return sb.toString();
    }
}

• 时间复杂度 O(mn)
• 空间复杂度 O(m + n)