题目链接

LeetCode
LeetCode

题目描述

数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中，第5位（从下标0开始计数）是5，第13位是1，第19位是4，等等。

请写一个函数，求任意第n位对应的数字。

解题思路

将 101112⋯ 中的每一位称为 数位 ，记为 n ；
将 10, 11, 12, ⋯ 称为 数字 ，记为 num ；
数字 10 是一个两位数，称此数字的 位数 为 2 ，记为 digit ；
每 digit 位数的起始数字（即：1, 10, 100,⋯），记为 start 。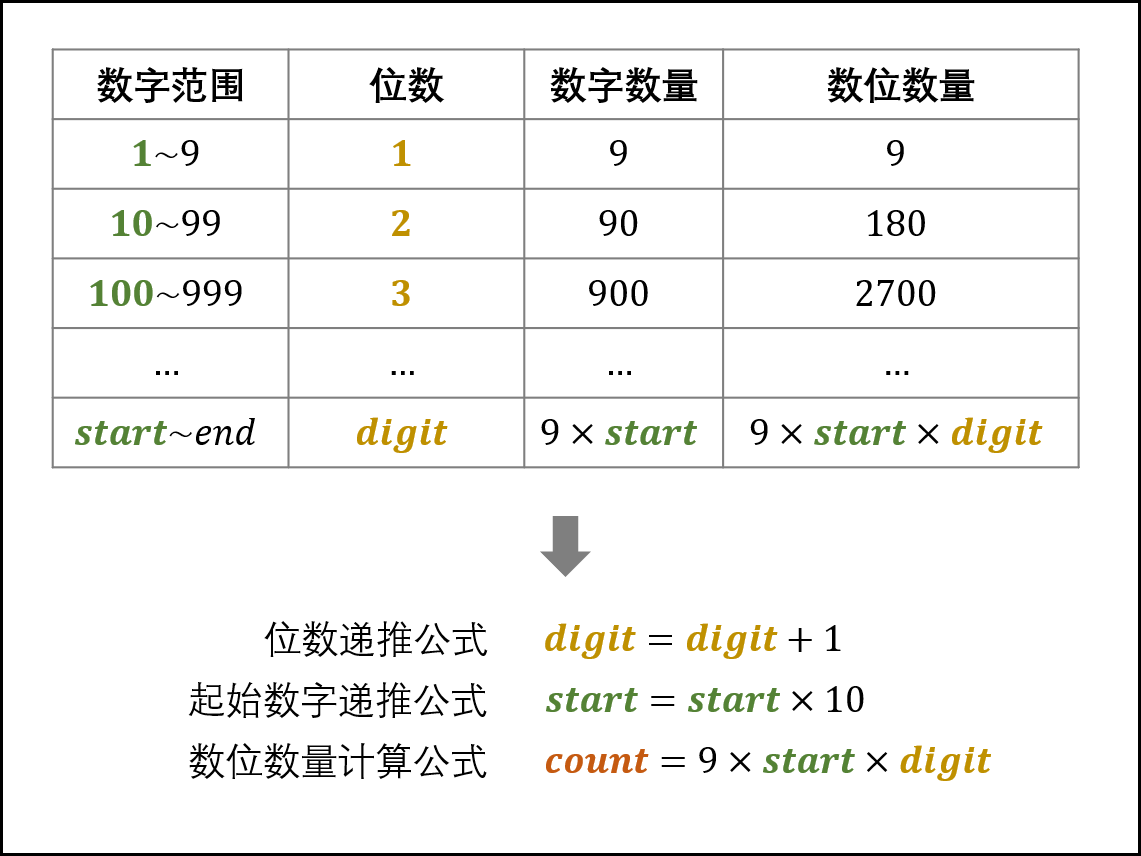

观察上表，可推出各 digit 下的数位数量 count 的计算公式：
count=9×start×digit
根据以上分析，可将求解分为三步：

1. 确定 n 所在 数字 的 位数 ，记为 digit ；
2. 确定 n 所在的 数字 ，记为 num ；
3. 确定 n 是 num 中的哪一数位，并返回结果。

1. 确定所求数位的所在数字的位数

如下图所示，循环执行 n 减去 一位数、两位数、… 的数位数量 count ，直至 n≤count 时跳出。

由于 n 已经减去了一位数、两位数、…、(digit-1) 位数的 数位数量 count ，因而此时的 n 是从起始数字 start 开始计数的。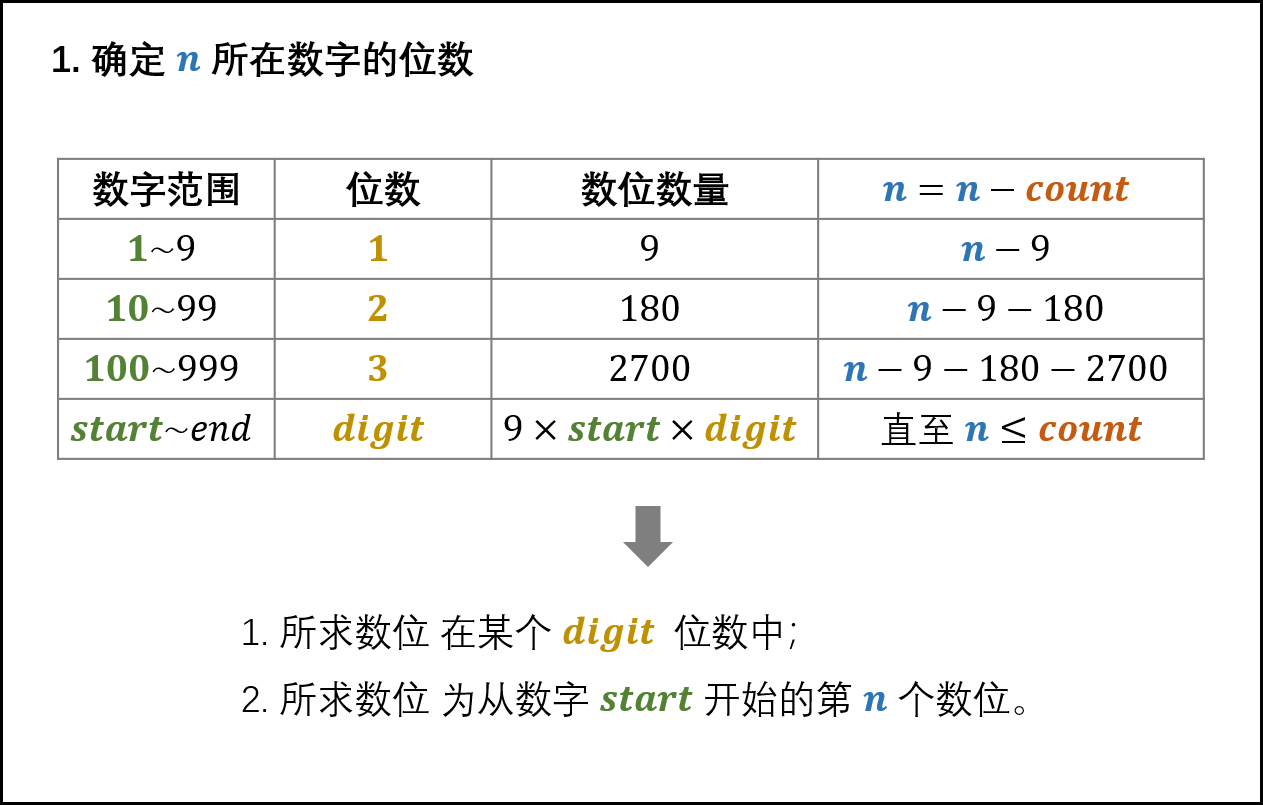

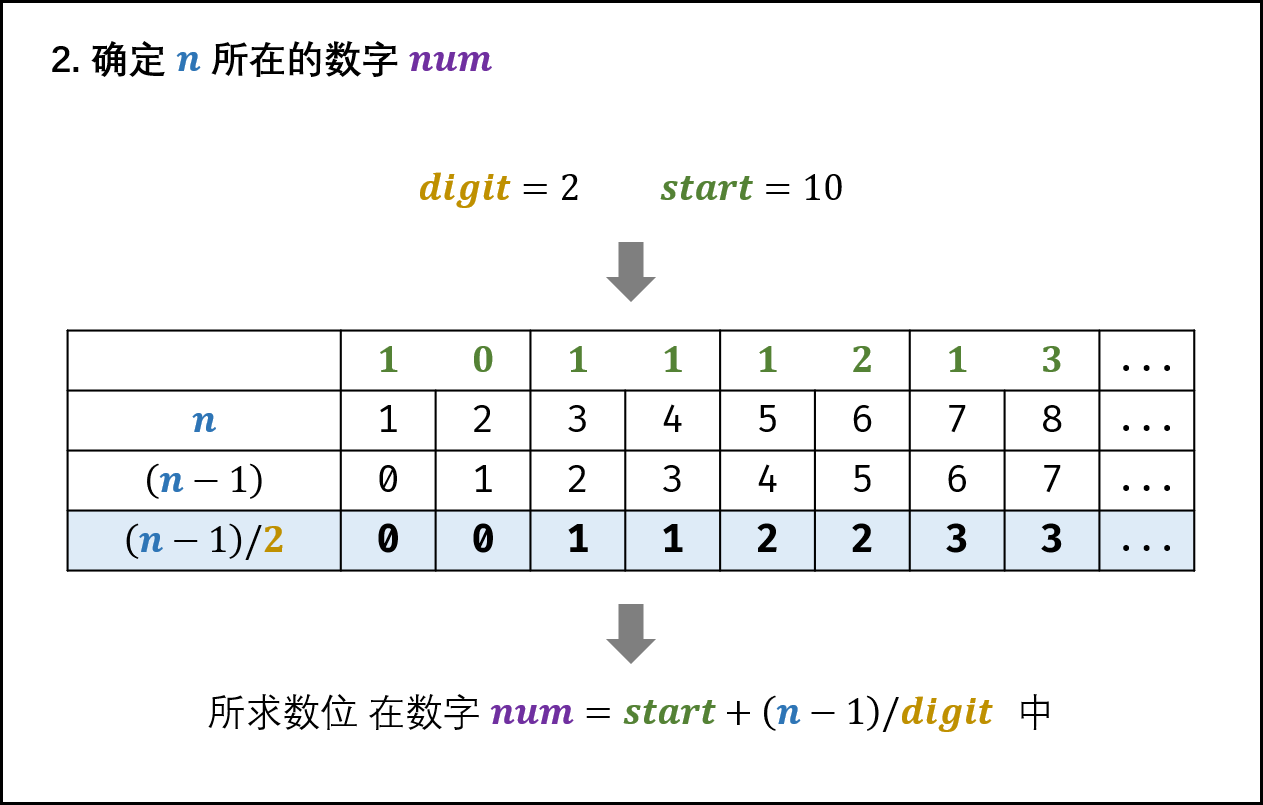
2. 确定所求数位所在的数字

如下图所示，所求数位 在从数字 start 开始的第 [(n - 1) / digit] 个 数字 中（ start 为第 0 个数字）。

num = start + (n - 1) / digit

结论： 所求数位在数字 num 中。

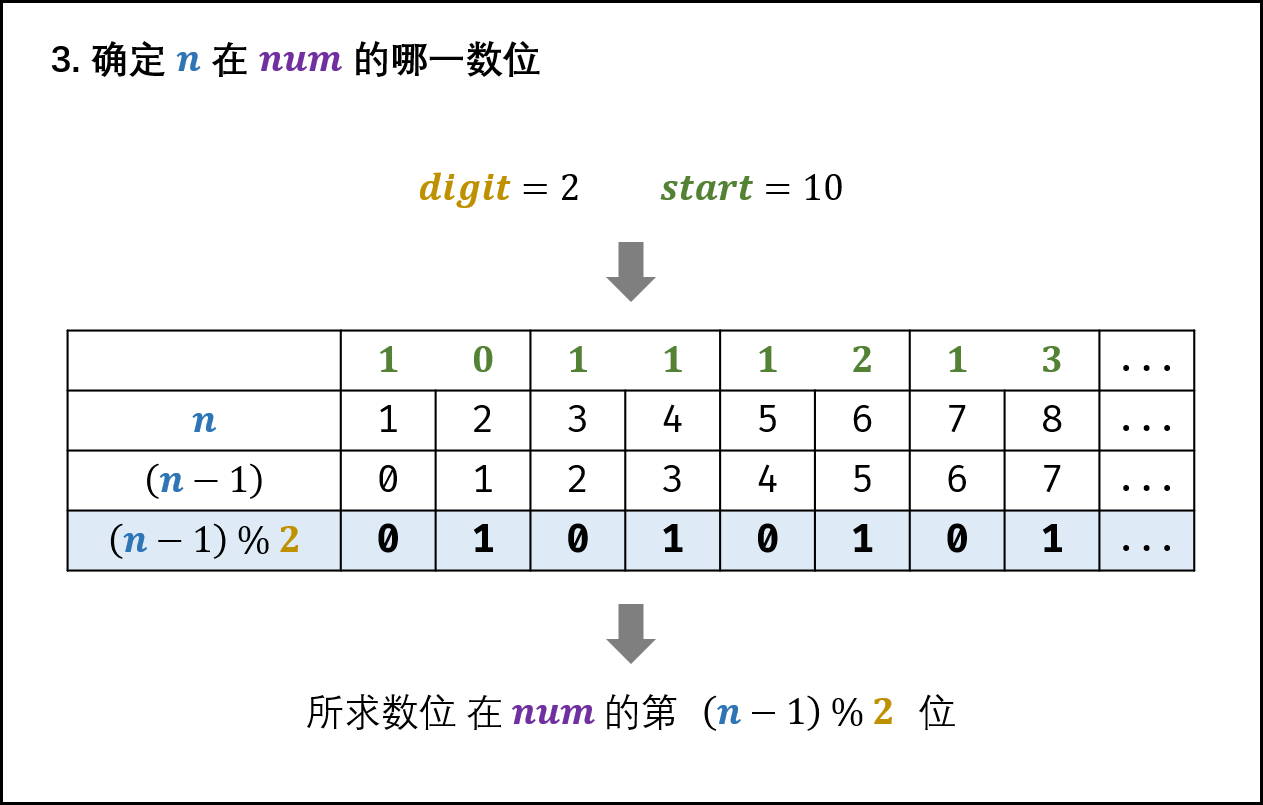
3. 确定所求数位在 num 的哪一数位

如下图所示，所求数位为数字 num 的第 (n−1)%digit 位（ 数字的首个数位为第 0 位）。

s = str(num) # 转化为 string
res = int(s[(n - 1) % digit]) # 获得 num 的 第 (n - 1) % digit 个数位，并转化为 int

结论： 所求数位是 res 。

class Solution {
public:
    int findNthDigit(int n) {
        if(n==0) return 0;
        int digit = 1; // 数位
        long start = 1; // 每 digit 位数的起始数字（即：1, 10, 100,⋯）
        long count = 9; // 每 digit 位数的结束数字（即：9, 99, 999,⋯）
        // 确定 n 所在 数字 的 位数
        while(n>count){
            n-=count; // 减去 
            digit+=1; // 位数递推 digit = digit + 1;
            start*=10; // 起始数字递推 start = start * 10 
            count=digit*start*9; // 计算当前位数数量
        }
        // 确定 n 所在的 数字
        long num  = start + (n-1) / digit;
        // 确定 n 是 num 中的哪一数位 从 0 开始
        int index = (n-1) % digit;
        string s = to_string(num);
        return s[index] - '0';
    }
};

class Solution {
    public int findNthDigit(int n) {
        long ten = 1, digit = 1;
        while(9 * ten * digit < n){
            n -= 9 * ten * digit;
            ten = ten * 10;
            ++digit;
        }
        long num = ten + (n - 1) / digit;
        n -= digit * ((n - 1) / digit);
        for(int i = 0; i < digit - n; ++i){
            num = num / 10;
        }
        return (int)num % 10;
    }
}

• 时间复杂度 O(logn) ： 所求数位 n 对应数字 num 的位数 digit 最大为 O(logn) ；第一步最多循环 O(logn) 次；第三步中将 num 转化为字符串使用 O(logn) 时间；因此总体为 O(logn) 。
• 空间复杂度 O(logn) ： 将数字 num 转化为字符串 str(num) ，占用 O(logn) 的额外空间。