题目链接

LeetCode

题目描述

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

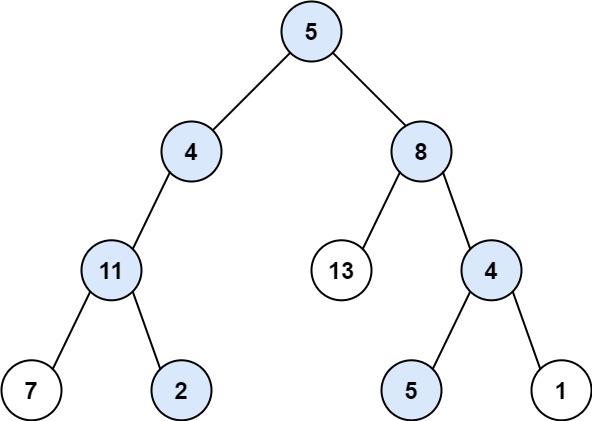
113. 路径总和 II - 图1

输入： root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出： [[5,4,11,2],[5,8,4,5]]

示例 2：

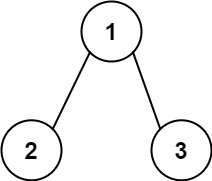
113. 路径总和 II - 图2

输入： root = [1,2,3], targetSum = 5
输出： []

示例 3：

输入： root = [1,2], targetSum = 0
输出： []

提示：

  • 树中节点总数在范围 [0, 5000] 内
  • -1000 <= Node.val <= 1000
  • -1000 <= targetSum <= 1000

解题思路：

方法一：深度优先遍历

我们可以采用深度优先搜索的方式，枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径。

  1. /**
  2.  * Definition for a binary tree node.
  3.  * struct TreeNode {
  4.  *     int val;
  5.  *     TreeNode *left;
  6.  *     TreeNode *right;
  7.  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  8.  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  9.  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  10.  * };
  11.  */
  12. class Solution {
  13. public:
  14.     vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
  15.         vector<int> v;
  16.         recur(root,targetSum,0);
  17.         return res;
  18.     }
  19.     void recur(TreeNode* root, int target,int sum){
  20.         if(root==nullptr)
  21.             return;
  22.         sum = sum + root->val;
  23.         path.push_back(root->val);
  24.         if(root->left==nullptr&&root->right==nullptr&&sum==target)
  25.             res.push_back(path);
  26.         recur(root->left,target,sum);
  27.         recur(root->right,target,sum);
  28.         path.pop_back();
  29.     }
  30. private:
  31. vector<vector<int>> res;
  32. vector<int> path;
  33. };
  1. class Solution {
  2.     List<List<Integer>> res;
  3.     List<Integer> path;
  4.     public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
  5.         res = new LinkedList<List<Integer>>();
  6.         path = new LinkedList<Integer>();
  7.         recur(root, targetSum);
  8.         return res;
  9.     }
  10.     private void recur(TreeNode root, int target){
  11.         if(root == null){
  12.             return;
  13.         }
  14.         path.add(root.val);
  15.         target = target - root.val;
  16.         if(root.left == null && root.right == null){
  17.             if(target == 0){
  18.                 res.add(new LinkedList<Integer>(path));
  19.             }
  20.         }else{
  21.             recur(root.left, target);
  22.             recur(root.right, target);
  23.         }
  24.         path.remove(path.size() - 1);
  25.     }
  26. }
  • 时间复杂度 O(n^2)：其中N是树的节点数
  • 空间复杂度 O(n)

    方法二：广度优先遍历

    我们也可以采用广度优先搜索的方式，遍历这棵树。当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径。
    为了节省空间，我们使用哈希表记录树中的每一个节点的父节点。每次找到一个满足条件的节点，我们就从该节点出发不断向父节点迭代，即可还原出从根节点到当前节点的路径。
    不怎么推荐