题目链接

LeetCode

题目描述

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

• s = s1 + s2 + ... + sn
• t = t1 + t2 + ... + tm
• |n - m| <= 1
• 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...

提示： a + b 意味着字符串 a 和 b 连接。

示例 1：

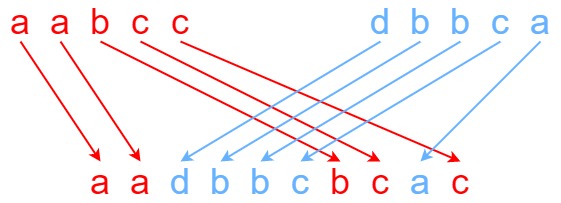
输入： s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
输出： true

示例 2：

输入： s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc”
输出： false

示例 3：

输入： s1 = “”, s2 =””, s3 = “”
输出： true

提示：

• 0 <= s1.length, s2.length <= 100
• 0 <= s3.length <= 200

• s1、s2、和 s3 都由小写英文字母组成
  

  解题思路

  方法一：动态规划

  我们定义 f(i, j) 表示 s_1的前 i 个元素和 s2的前 j 个元素是否能交错组成 s3的前 i + j 个元素。如果 s1的第 i 个元素和 s3的第 i + j 个元素相等，那么 s1的前 i 个元素和 s2的前 j 个元素是否能交错组成 s3的前 i + j 个元素取决于 s1的前 i - 1 个元素和 s2的前 jj 个元素是否能交错组成 s3的前 i + j - 1 个元素，即此时 f(i, j) 取决于 f(i - 1, j)，在此情况下如果 f(i - 1, j) 为真，则 f(i, j) 也为真。同样的，如果 s2的第 j 个元素和 s3 的第 i + j 个元素相等并且 f(i, j - 1) 为真，则 f(i, j) 也为真。于是我们可以推导出这样的动态规划转移方程：
  
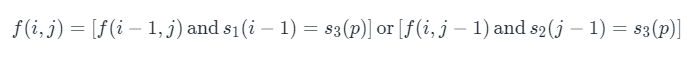
  其中 p = i + j - 1。边界条件为 f(0,0)=True。

  class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        if(s1.length() + s2.length() != s3.length()){
            return false;
        }
        boolean[][] dp = new boolean[s1.length() + 1][s2.length() + 1];
        dp[0][0] = true;
        for(int i = 0; i <= s1.length() ;++i){
            for(int j = 0; j <= s2.length(); ++j){
                int p = i + j - 1;
                if(i > 0){
                    dp[i][j] |= dp[i-1][j]&&s1.charAt(i-1) == s3.charAt(p);
                } 
                if(j > 0){
                    dp[i][j] |= dp[i][j-1]&&s2.charAt(j-1) == s3.charAt(p);
                }
            }
        }
        return dp[s1.length()][s2.length()];
    }
  }

  
  

• 时间复杂度 O(nm)

• 空间复杂度 O(nm)