题目链接

LeetCode

题目描述

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

  • 每个孩子至少分配到 1 个糖果。
  • 评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果。

那么这样下来，老师至少需要准备多少颗糖果呢？

示例 1：

输入： [1,0,2]
输出： 5
解释： 你可以分别给这三个孩子分发 2、1、2 颗糖果。

示例 2：

输入： [1,2,2]
输出： 4
解释： 你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果，这已满足上述两个条件。

解题思路

方法一：两遍遍历

第一遍从左到右遍历 如果当前坐标左边的值小于当前值 当前糖果需要 左边分发的糖果数加一，否则可以发一个
第二遍从右向左遍历 如果当前坐标右边的值小于当前值 当前糖果需要 右边分发的糖果数加一，否则可以发一个
每个位置取两次遍历需要发的最小糖果数中的最大值（因为需要满足评分比左右高的同学得到的糖果比左右多条件）

  1. class Solution {
  2.     public int candy(int[] ratings) {
  3.         int n = ratings.length;
  4.         int res = 0;
  5.         int[] left = new int[n];
  6.         for(int i = 0; i < n; ++i){
  7.             if(i > 0 && ratings[i] > ratings[i - 1]){
  8.                 left[i] = left[i - 1] + 1;
  9.             }else{
  10.                 left[i] = 1;
  11.             }
  12.         }
  13.         // int[] right = new int[n];
  14.         // for(int i = n-1; i >= 0; --i){
  15.         //     if(i < n-1 && ratings[i] > ratings[i + 1]){
  16.         //         right[i] = right[i + 1] + 1;
  17.         //     }else{
  18.         //         right[i] = 1;
  19.         //     }
  20.         //     res += Math.max(left[i],right[i]);
  21.         // }
  22.         int right = 0;
  23.         for(int i = n-1; i >= 0; --i){
  24.             if(i < n-1 && ratings[i] > ratings[i + 1]){
  25.                 right = right + 1;
  26.             }else{
  27.                 right = 1;
  28.             }
  29.             res += Math.max(left[i],right);
  30.         }
  31.         return res;
  33.     }
  34. }
  • 时间复杂度 O(n)
  • 空间复杂度 O(n)

    方法二：常数空间遍历

思路及解法
注意到糖果总是尽量少给，且从 1 开始累计，每次要么比相邻的同学多给一个，要么重新置为 1。依据此规则，我们可以画出下图：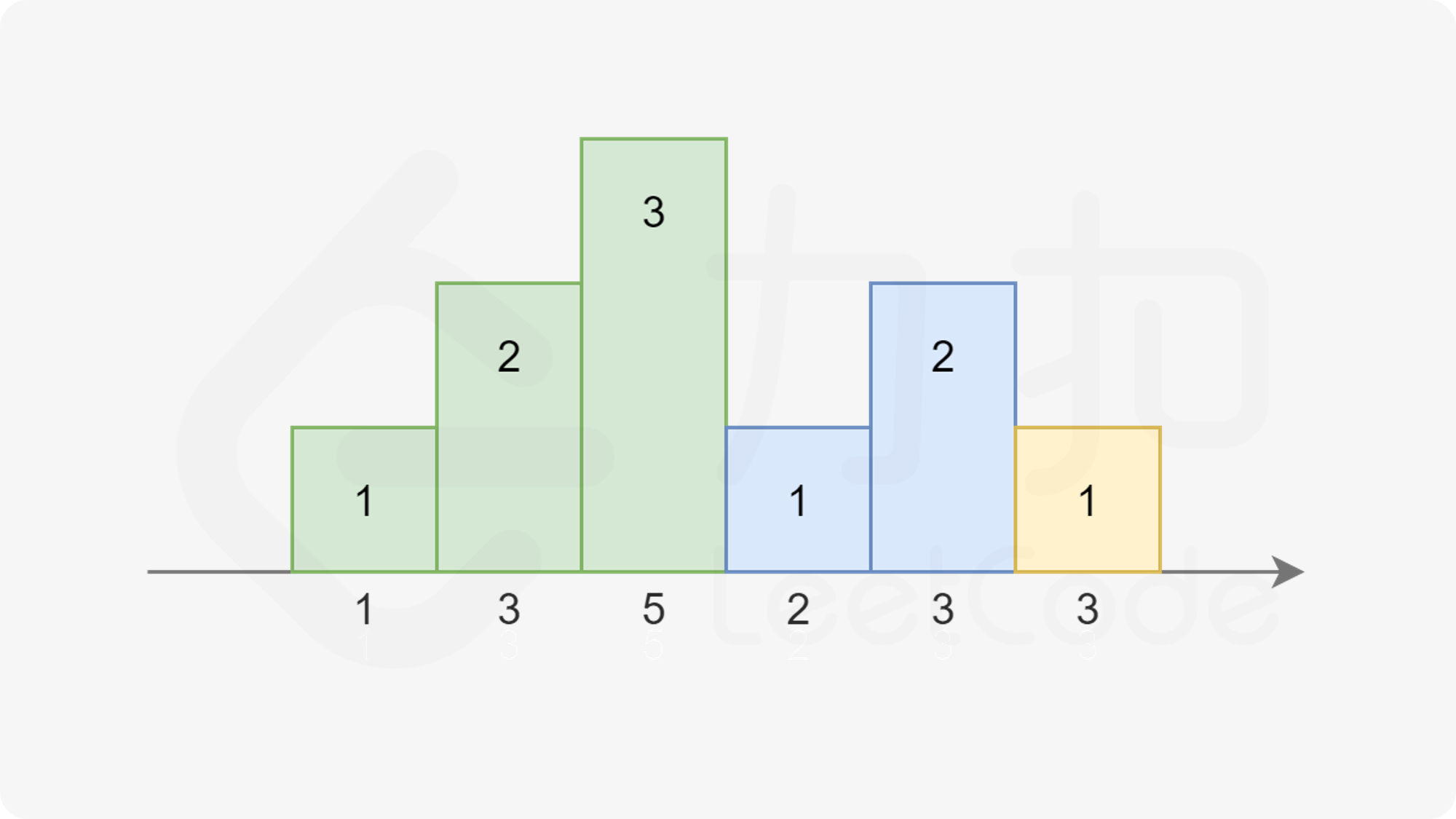
135. 分发糖果** - 图1
其中相同颜色的柱状图的高度总恰好为 1,2,3…。
而高度也不一定一定是升序，也可能是 3,2,1… 的降序：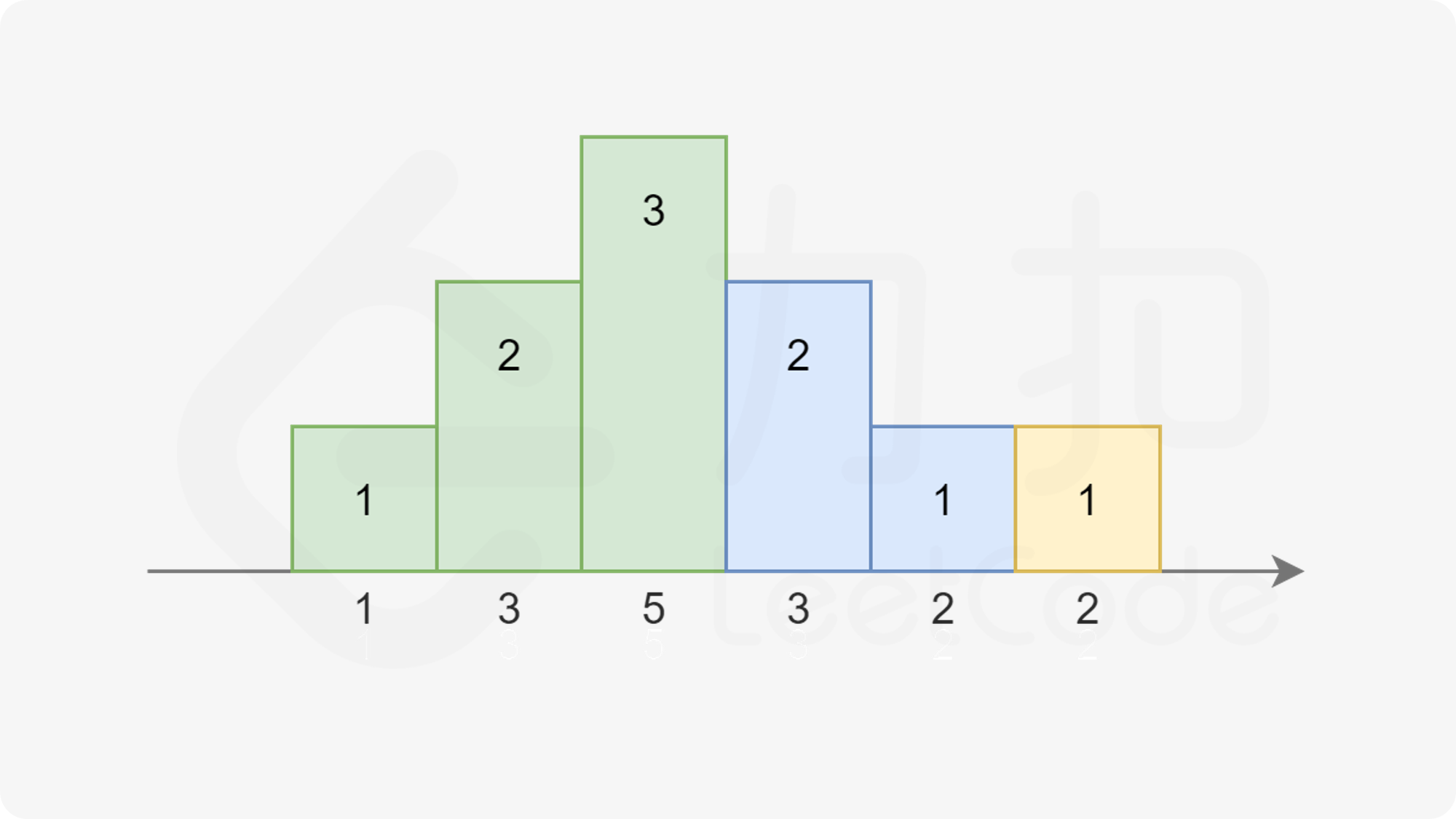
135. 分发糖果** - 图2
注意到在上图中，对于第三个同学，他既可以被认为是属于绿色的升序部分，也可以被认为是属于蓝色的降序部分。因为他同时比两边的同学评分更高。我们对序列稍作修改：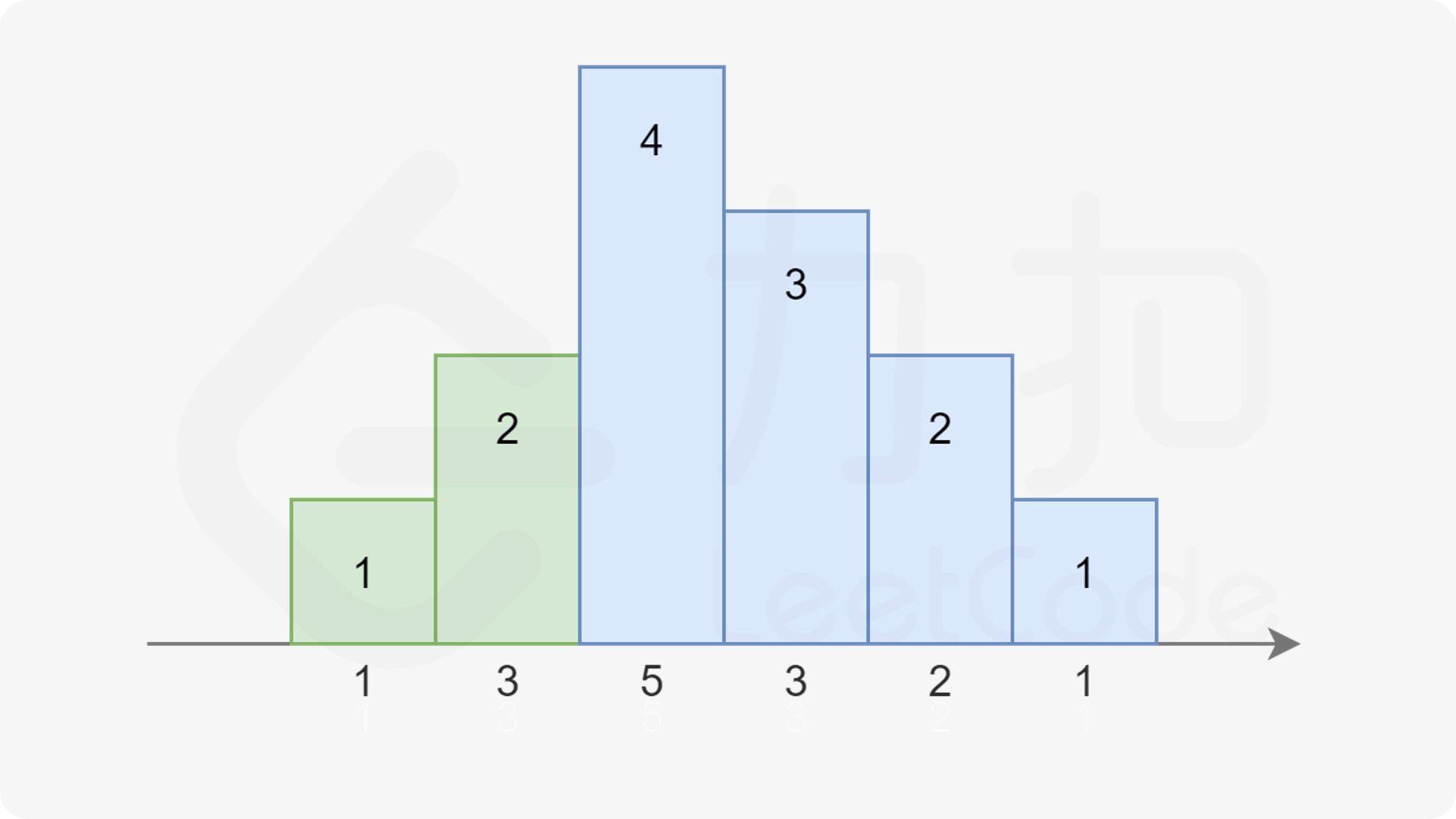
135. 分发糖果** - 图3
注意到右边的升序部分变长了，使得第三个同学不得不被分配 44 个糖果。

依据前面总结的规律，我们可以提出本题的解法。我们从左到右枚举每一个同学，记前一个同学分得的糖果数量为 pre：

  • 如果当前同学比上一个同学评分高，说明我们就在最近的递增序列中，直接分配给该同学 pre+1 个糖果即可。

  • 否则我们就在一个递减序列中，我们直接分配给当前同学一个糖果，并把该同学所在的递减序列中所有的同学都再多分配一个糖果，以保证糖果数量还是满足条件。

    • 我们无需显式地额外分配糖果，只需要记录当前的递减序列长度，即可知道需要额外分配的糖果数量。
    • 同时注意当当前的递减序列长度和上一个递增序列等长时，需要把最近的递增序列的最后一个同学也并进递减序列中。
    • 在递增序列中，如果当前孩子和上一个孩子的评分相等，当前孩子最少可以获得一个糖果，因为当前孩子评分不大于上一个孩子，最少原则，可以给最少一个

这样，我们只要记录当前递减序列的长度 dec，最近的递增序列的长度 inc 和前一个同学分得的糖果数量 pre 即可。

  1. class Solution {
  2.     public int candy(int[] ratings) {
  3.         int n = ratings.length;
  4.         int res = 1, pre = 1, inc = 1, dec = 0;
  5.         for(int i = 1; i < n; ++i){
  6.             if(ratings[i] >= ratings[i - 1]){
  7.                 dec = 0;
  8.                 // 如果和上一个孩子的评分相等，当前孩子可以获得一个糖果，因为当前孩子评分不大于上一个孩子
  9.                 // 最少原则，可以给最少一个
  10.                 pre = ratings[i] == ratings[i-1] ? 1 : pre + 1;
  11.                 res += pre;
  12.                 // 最近递增序列为当前需要发的糖果数
  13.                 inc = pre;
  14.             }else{
  15.                 // 当前递减序列长度加上当前孩子
  16.                 ++dec;
  17.                 // 如果当前递减序列长度等于最近的递增序列长度，将最后一个递增元素也就是第一个递减元素加入
  18.                 // 最后一个递增元素加一
  19.                 if(dec == inc){
  20.                     ++dec;
  21.                 }
  22.                 res += dec;
  23.                 // 当前孩子最少一个糖果
  24.                 pre = 1;
  25.                 // inc 在上一个分支中更新
  26.             }
  27.         }
  28.         return res;
  29.     }
  30. }
  • 时间复杂度 O(n)
  • 空间复杂度 O(1)