题目链接

题目描述

字典 wordList 中从单词 beginWord和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk：

每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord不需要在 wordList 中。
sk == endWord

给你两个单词 beginWord和 endWord 和一个字典 wordList ，返回从 _beginWord_ 到 _endWord_ 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0 。

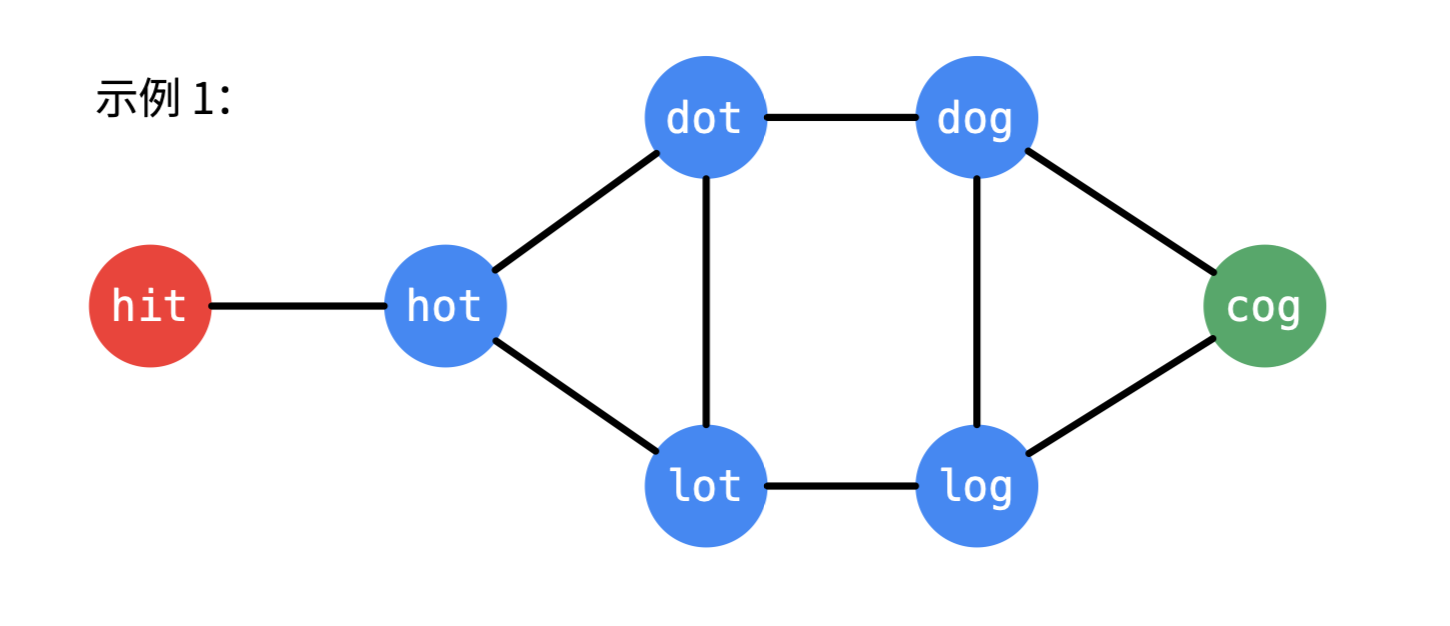
示例 1：

输入： beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”,”cog”]
输出： 5
解释： 一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的长度 5。

示例 2：

输入： beginWord = “hit”, endWord = “cog”, wordList = [“hot”,”dot”,”dog”,”lot”,”log”]
输出： 0
解释： endWord “cog” 不在字典中，所以无法进行转换。

提示：

1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同

解题思路

方法一：BFS
「转换」意即：两个单词对应位置只有一个字符不同，例如 “hit” 与 “hot”，这种转换是可以逆向的，因此，根据题目给出的单词列表，可以构建出一个无向（无权）图；

127. 单词接龙*** - 图1

如果一开始就构建图，每一个单词都需要和除它以外的另外的单词进行比较，复杂度是 O(NwordLen)，这里 N 是单词列表的长度；
为此，我们在遍历一开始，把所有的单词列表放进一个哈希表中，然后在遍历的时候构建图，每一次得到在单词列表里可以转换的单词，复杂度是 O(26×wordLen)，借助哈希表，找到邻居与 N 无关；

使用 BFS 进行遍历，需要的辅助数据结构是：

队列；

visited 集合。说明：可以直接在 wordSet (由 wordList 放进集合中得到)里做删除。但更好的做法是新开一个哈希表，遍历过的字符串放进哈希表里。这种做法具有普遍意义。绝大多数在线测评系统和应用场景都不会在意空间开销。

class Solution {
// 存放所有未被用的字符串
Set<String> wordSet;
// 存放中间已用字符串
Queue<String> q;
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
   // 第 1 步：先将 wordList 放到哈希表里，便于判断某个单词是否在 wordList 里
   wordSet = new HashSet<String>();
   for(String s : wordList){
       wordSet.add(s);
   }
   // 如果不包含 endWord
   if(!wordSet.contains(endWord)){
       return 0;
   }
   // 删除开始字符串
   wordSet.remove(beginWord);
   // 将开始字符串加入队列
   q = new LinkedList<String>();
   q.offer(beginWord);
   // 开始广度优先遍历，包含起点，因此初始化的时候步数为 1
   int step = 1;
   while(!q.isEmpty()){
       // 遍历当前所有步数为 step 的单词
       int curWordSize = q.size();
       for(int i = 0; i < curWordSize; ++i){
           // 依次遍历当前队列中的单词
           String curWord = q.poll();
           // 如果 currentWord 能够修改 1 个字符与 endWord 相同，则返回 step + 1
           if(bfs(curWord, endWord)){
               return step + 1;
           }
       }
       // 否则加一步，遍历下一个step
       ++step;
   }
   return 0;
}
private boolean bfs(String curWord, String endWord){
   char[] charArr = curWord.toCharArray();
   // 尝试对 currentWord 修改每一个字符，看看是不是能与 endWord 匹配
   for(int i = 0; i < endWord.length(); ++i){
       // 先保存当前位置字符，然后恢复
       char originChar = charArr[i];
       for(char j = 'a'; j <= 'z'; ++j){
           // 如果当前位置相同，跳过，没修改
           if(j == charArr[i]){
               continue;
           }
           // 修改字符
           charArr[i] = j;
           String nextWord = String.valueOf(charArr);
           // 如果 wordSet 中存在改变一个字符的字符串
           if(wordSet.contains(nextWord)){
               // 如果是 endWord，直接返回 true
               if(nextWord.equals(endWord)){
                   return true;
               }
               // 将下个字符串存入队列
               q.offer(nextWord);
               // 将下个字符串从 wordSet 中删除
               wordSet.remove(nextWord);
           }
       }
       charArr[i] = originChar;
   }
   return false;
}
}

时间复杂度 O(n)
空间复杂度 O(n)

127. 单词接龙***

题目链接

题目描述

解题思路

方法一：BFS