题目链接

LeetCode

题目描述

路径 被定义为一条从树中任意节点出发，沿父节点 - 子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

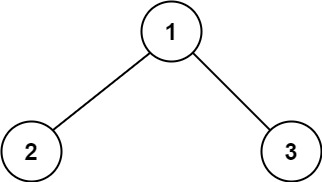
124. 二叉树中的最大路径和* - 图1

输入： root = [1,2,3]
输出： 6
解释： 最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

124. 二叉树中的最大路径和* - 图2

输入： root = [-10,9,20,null,null,15,7]
输出： 42
解释： 最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

  • 树中节点数目范围是 [1, 3 * 104]
  • -1000 <= Node.val <= 1000

    解题思路

    方法一：递归+自底向上

    ```cpp class Solution { private: int maxSum = INT_MIN;

public: int maxGain(TreeNode* node) { if (node == nullptr) { return 0; }

  1.     // 递归计算左右子节点的最大贡献值
  2.     // 只有在最大贡献值大于 0 时，才会选取对应子节点
  3.     int leftGain = max(maxGain(node->left), 0);
  4.     int rightGain = max(maxGain(node->right), 0);
  5.     // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
  6.     int priceNewpath = node->val + leftGain + rightGain;
  7.     // 更新答案
  8.     maxSum = max(maxSum, priceNewpath);
  9.     // 返回节点的最大贡献值
  10.     return node->val + max(leftGain, rightGain);
  11. }
  13. int maxPathSum(TreeNode* root) {
  14.     maxGain(root);
  15.     return maxSum;
  16. }

}; ```

  • 时间复杂度 O(n)
  • 空间复杂度 O(n)