题目链接

牛客网
LeetCode

题目描述

从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

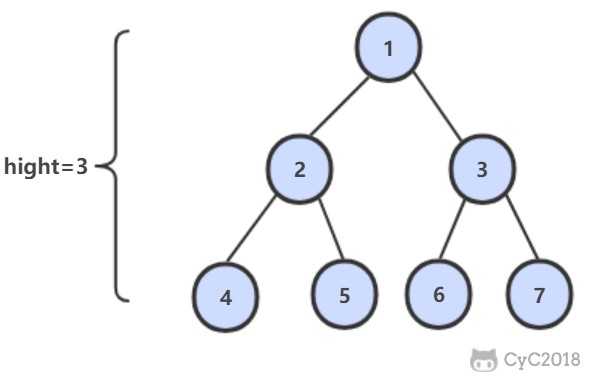
解题思路

方法一（分治法）

分治法简介：求一个规模为n的问题，先求左边规模大约为n/2的问题，再求右边规模大约为n/2的问题，然后合并左边，右边的解，从而求得最终解。具体可参考归并排序。

1. 终止条件： 当 root 为空，说明已越过叶节点，因此返回 深度 00 。
2. 递推工作： 本质上是对树做后序遍历。
   1. 计算节点 root 的 左子树的深度 ，即调用 maxDepth(root.left)；
   2. 计算节点 root 的 右子树的深度 ，即调用 maxDepth(root.right)；
3. 返回值： 返回 此树的深度 ，即 max(maxDepth(root.left), maxDepth(root.right)) + 1。

`

`

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
public:
    int TreeDepth(TreeNode* pRoot)
    {
        if(pRoot==nullptr)
            return 0;
        return max(TreeDepth(pRoot->left), TreeDepth(pRoot->right))+1;
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        return deep(root);
    }
    int deep(TreeNode* root,int d = 0){
        if(root == nullptr){
            return d;
        }
        return max(deep(root->left,d+1),deep(root->right,d+1));
    }
};

• 时间复杂度 O(N) ： N 为树的节点数量，计算树的深度需要遍历所有节点。

• 空间复杂度 O(N) ： 最差情况下（当树退化为链表时），递归深度可达到 N 。

  方法二（层次遍历）

• 树的层序遍历 / 广度优先搜索往往利用 队列 实现。

• 关键点： 每遍历一层，则计数器 +1 ，直到遍历完成，则可得到树的深度。

  算法解析：

1. 特例处理： 当 root 为空，直接返回 深度 0 。
2. 初始化： 队列 queue （加入根节点 root ），计数器 res = 0。
3. 循环遍历： 当 queue 为空时跳出。
   1. 记录当前层中结点个数
   2. 遍历队列： 遍历 queue 中的各节点 node ，并将其左子节点和右子节点加入 tmp；
   3. 统计层数： 执行 res += 1 ，代表层数加 1；
4. 返回值： 返回 res 即可。

   /**
   * Definition for a binary tree node.
   * struct TreeNode {
   *     int val;
   *     TreeNode *left;
   *     TreeNode *right;
   *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
   * };
   */
   class Solution {
   public:
    int maxDepth(TreeNode* root) {
        if(root==NULL)
            return 0;
        return recur(root);
    }
   private:
    int recur(TreeNode* root){
        int k=0;
        queue<TreeNode*> qu;
        qu.push(root);
        while(!qu.empty()){
            int sz = qu.size();
            while(sz--){
                TreeNode* node = qu.front();
                qu.pop();
                if(node->left)
                    qu.push(node->left);
                if(node->right)
                    qu.push(node->right);
            } 
            k++;
        }
        return k;
    }
   };
   

   /**
   * Definition for a binary tree node.
   * struct TreeNode {
   *     int val;
   *     TreeNode *left;
   *     TreeNode *right;
   *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
   * };
   */
   class Solution {
   public:
    int maxDepth(TreeNode* root) {
        if(root==NULL)
            return 0;
        return recur(root);
    }
   private:
    int recur(TreeNode* root){
        int k=1;
        queue<TreeNode*> qu;
        bool visited = false;
        qu.push(root);
        while(!qu.empty()){
            int sz = qu.size();
            while(sz--){
                TreeNode* node = qu.front();
                qu.pop();
                if(node->left){
                    qu.push(node->left);
                    visited=true;
                }  
                if(node->right){
                    qu.push(node->right);
                    visited=true;
                }
            } 
            if(visited){
                k++;
                visited = false;
            }else{
                return k;
            }
        }
        return k;
    }
   };
   

• 时间复杂度 O(N) ： N 为树的节点数量，计算树的深度需要遍历所有节点。
• 空间复杂度 O(N) ： 最差情况下（当树平衡时），队列 queue 同时存储 N/2 个节点。