题目链接

LeetCode

题目描述

把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

限制：
1 <= n <= 11

解题思路

动态规划

题目需要我们求出所有点数出现的概率，根据概率的计算公式，点数 k 出现概率就算公式为：
P(k)=k出现的次数/总次数
投掷 n 个骰子，所有点数出现的总次数是 6^n ，因为一共有 n 枚骰子，每枚骰子的点数都有 6 种可能出现的情况。
我们的目的就是 计算出投掷完 n 枚骰子后每个点数出现的次数。

• 首先用数组的第一维来表示阶段，也就是投掷完了几枚骰子。
• 然后用第二维来表示投掷完这些骰子后，可能出现的点数。
• 数组的值就表示，该阶段各个点数出现的次数。

所以状态表示就是这样的：dp[i][j] ，表示投掷完 i 枚骰子后，点数 j 的出现次数。

找出状态转移方程

找状态转移方程也就是找各个阶段之间的转化关系，同样我们还是只需分析最后一个阶段，分析它的状态是如何得到的。
最后一个阶段也就是投掷完 n 枚骰子后的这个阶段，我们用 dp[n][j] 来表示最后一个阶段点数 j 出现的次数。

单单看第 n 枚骰子，它的点数可能为 1, 2, 3, … , 6，因此投掷完 n 枚骰子后点数 j 出现的次数，可以由投掷完 n-1 枚骰子后，对应点数 j-1, j-2, j-3, … , j-6 出现的次数之和转化过来。

for (第n枚骰子的点数 i = 1; i <= 6; i ++) {
    dp[n][j] += dp[n-1][j - i]
}

写成数学公式是这样的：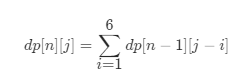

代码：

class Solution {
public:
    vector<double> dicesProbability(int n) {
        //定义一个数组保存所有状态，一维是第n次时，二维为第n次时所有可能情况
        int dp[12][70]={0};
        //我们只能知道第一次的情况，也是边界条件
        for(int i=1;i<=6;i++)
            dp[1][i]=1;
        // 一层循环，每多一个色子的情况
        for (int i = 2; i <= n; i ++) {
            //二层循环是这么多色子情况下的所有可能和
            for (int j = i; j <= 6*i; j ++) {
                //三层循环是为了找到能得到这种可能和时，对于少一个色子时的所有可能情况，相加即是当前可能总和
                for (int cur = 1; cur <= 6; cur ++) {
                    //i-1,即是对于只有对于少一个色子时，最小和最少为i-1，不可能再小了
                    if (j - cur <= 0) {
                        break;
                    }
                    dp[i][j] += dp[i-1][j-cur];
                }
            }
        }
        int all = pow(6, n);
        vector<double> ret;
        for (int i = n; i <= 6 * n; i ++) {
            ret.push_back(dp[n][i] * 1.0 / all);
        }
        return ret;
    }
};

空间优化

我们知道，每个阶段的状态都只和它前一阶段的状态有关，因此我们不需要用额外的一维来保存所有阶段。
用一维数组来保存一个阶段的状态，然后对下一个阶段可能出现的点数 j 从大到小遍历，实现一个阶段到下一阶段的转换。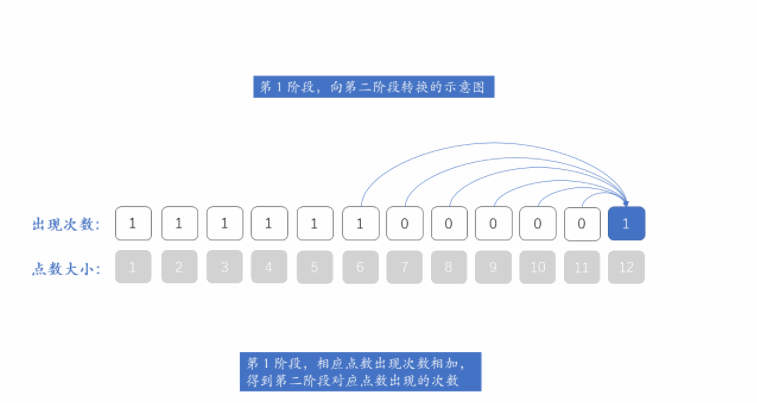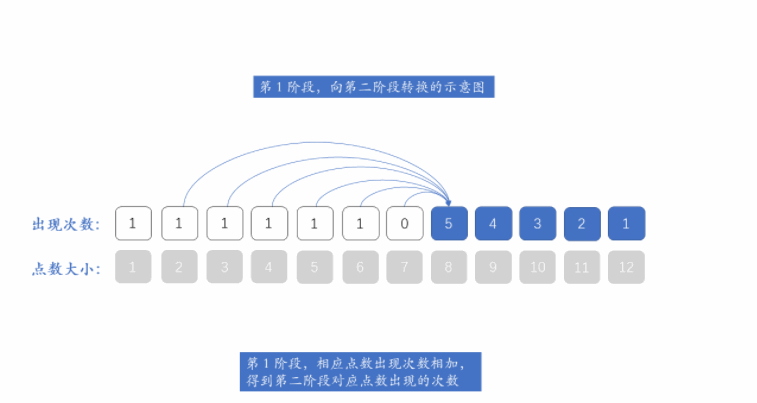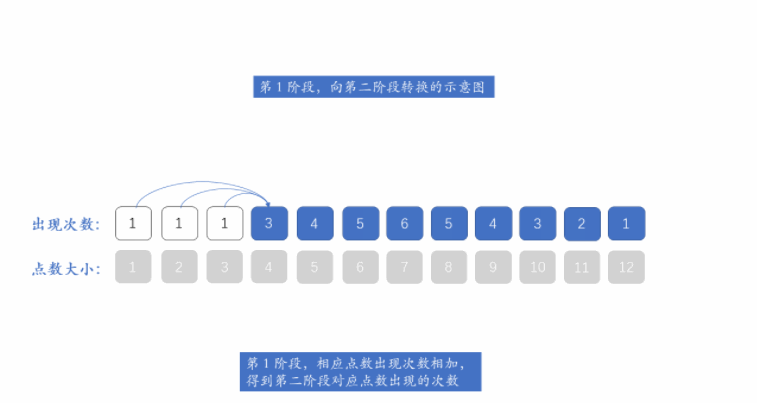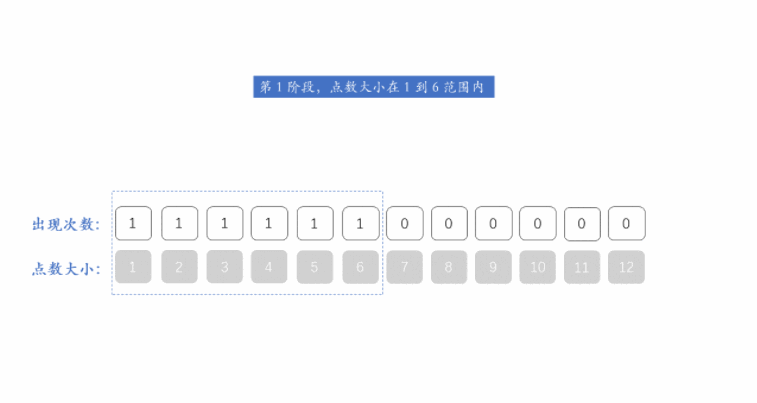

代码：

class Solution {
public:
    vector<double> dicesProbability(int n) {
        int dp[70];
        memset(dp, 0, sizeof(dp));
        for (int i = 1; i <= 6; i ++) {
            dp[i] = 1;
        }
        for (int i = 2; i <= n; i ++) {
            for (int j = 6*i; j >= i; j --) {
                dp[j] = 0;
                for (int cur = 1; cur <= 6; cur ++) {
                    //i-1,即是对于只有对于少一个色子时，最小和最少为i-1，不可能再小了
                    if (j - cur < i-1) {
                        break;
                    }
                    dp[j] += dp[j-cur];
                }
            }
        }
        int all = pow(6, n);
        vector<double> ret;
        for (int i = n; i <= 6 * n; i ++) {
            ret.push_back(dp[i] * 1.0 / all);
        }
        return ret;
    }
};