题目链接

LeetCode

题目描述

二维矩阵 grid 由 0 （土地）和 1 （水）组成。岛是由最大的 4 个方向连通的 0 组成的群，封闭岛是一个 完全 由 1 包围（左、上、右、下）的岛。

请返回 封闭岛屿 的数目。

示例 1：

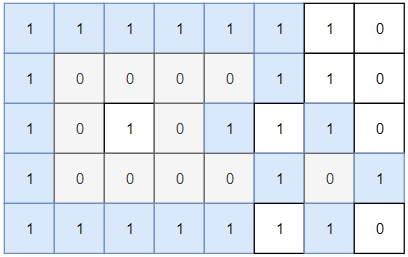
1254. 统计封闭岛屿的数目 - 图1

输入： grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出： 2
解释：
灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

示例 2：

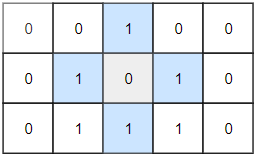
1254. 统计封闭岛屿的数目 - 图2

输入： grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
输出： 1

示例 3：

输入： grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
输出： 2

提示：

  • 1 <= grid.length, grid[0].length <= 100

  • 0 <= grid[i][j] <=1

    解题思路

    方法一：深度优先遍历

    首先遍历最外围土地，连接最外围土地的岛屿一定不是封闭岛屿，遍历并记录这些土地。
    然后遍历内围土地，在内围土地中，未被标记的均属于封闭岛屿。

    1. class Solution {
    2.   public int closedIsland(int[][] grid) {
    3.       int res = 0;
    4.       int row = grid.length, col = grid[0].length;
    5.       // 遍历外围，深度优先搜索，将所有非封闭岛屿全部设为 -1
    6.       for(int i = 0; i < row; ++i){
    7.           if(grid[i][0] == 0){
    8.               backstrack(grid, i, 0, 0, -1);
    9.           }
    10.           if(grid[i][col - 1] == 0){
    11.               backstrack(grid, i, col - 1, 0, -1);
    12.           }
    13.       }
    14.       for(int i = 1; i < col - 1; ++i){
    15.           if(grid[0][i] == 0){
    16.               backstrack(grid, 0, i, 0, -1);
    17.           }
    18.           if(grid[row - 1][i] == 0){
    19.               backstrack(grid, row - 1, i, 0, -1);
    20.           }
    21.       }
    22.       // 遍历内围，深度优先搜索，将所有封闭岛屿全部设为 2
    23.       for(int i = 1; i < grid.length - 1; ++i){
    24.           for(int j = 1; j < grid[0].length - 1; ++j){
    25.               if(grid[i][j] == 0){
    26.                   ++res;
    27.                   backstrack(grid, i, j, 0, 2);
    28.               }
    29.           }
    30.       }
    31.       return res;
    32.   }
    33.   // 深度优先遍历， 将所有 val 改为 target
    34.   private void backstrack(int[][] grid, int i, int j, int val, int target){
    35.       if(i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] != val){
    36.           return;
    37.       }
    38.       grid[i][j] = target;
    39.       backstrack(grid, i + 1, j, val, target);
    40.       backstrack(grid, i - 1, j, val, target);
    41.       backstrack(grid, i, j + 1, val, target);
    42.       backstrack(grid, i, j - 1, val, target);
    43.   }
    44. }

  • 时间复杂度：O(m*n)

  • 空间复杂度：O(1)