题目链接

LeetCode

题目描述

峰值元素是指其值大于左右相邻值的元素。

给你一个输入数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

示例 1：

输入： nums = [1,2,3,1]
输出： 2
解释： 3 是峰值元素，你的函数应该返回其索引 2。

示例 2：

输入： nums = [1,2,1,3,5,6,4]
输出： 1 或 5
解释： 你的函数可以返回索引 1，其峰值元素为 2；
或者返回索引 5， 其峰值元素为 6。

提示：

  • 1 <= nums.length <= 1000
  • -231 <= nums[i] <= 231 - 1
  • 对于所有有效的 i 都有 nums[i] != nums[i + 1]

进阶： 你可以实现时间复杂度为 O(logN) 的解决方案吗？

解题思路

方法一：线性扫描

本方法利用了连续的两个元素 nums[j] 和 nums[j + 1] 不会相等这一事实。于是，我们可以从头开始遍历 nums 数组。每当我们遇到数字 nums[i]，只需要检查它是否大于下一个元素 nums[i+1] 即可判断 nums[i] 是否是峰值。可以通过分别讨论问题的全部三种可能情况来理解本方法的思路。

情况 1. 所有的数字以降序排列。这种情况下，第一个元素即为峰值。我们首先检查当前元素是否大于下个元素。第一个元素满足这一条件，因此被正确判断为峰值。此时，我们不需要继续向下判断，也就不会有需要判断 nums[i] 和上一个元素 nums[i-1] 的大小的情况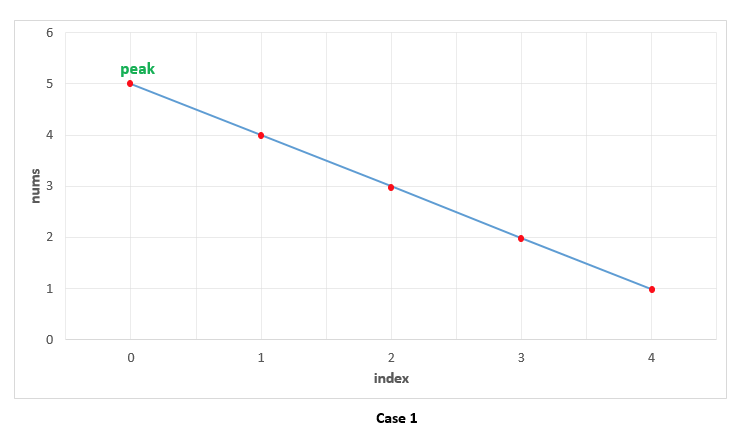
162. 寻找峰值** - 图1
情况 2. 所有的数字以升序排列。这种情况下，我们会一直比较 nums[i] 与 nums[i+1] 以判断 nums[i]nums[i] 是否是峰值元素。没有元素符合这一条件，说明处于上坡而非峰值。于是，在结尾，我们返回末尾元素作为峰值元素，得到正确结果。在这种情况下，我们同样不需要比较 nums[i] 和上一个元素 nums[i-1]，因为处于上坡是 nums[i] 不是峰值的充分条件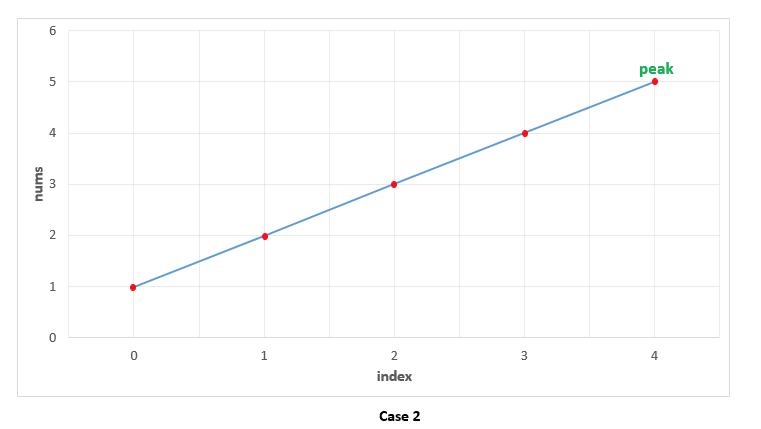
162. 寻找峰值** - 图2
情况 3. 峰值出现在中间某处。这种情况下，当遍历上升部分时，与情况 2 相同，没有元素满足 nums[i] > nums[i + 1]。我们不需要比较 nums[i] 和上一个元素 nums[i-1]。当到达峰值元素时，nums[i] > nums[i + 1] 条件满足。此时，我们同样不需要比较 nums[i] 和上一个元素 nums[i-1]。这是由于“遍历会到达第i个元素”本身就说明上一个元素（第i- 1个）不满足 nums[i] > nums[i + 1] 这一条件，也就说明 nums[i-1] < nums[i]。于是，我们同样可以得到正确结果。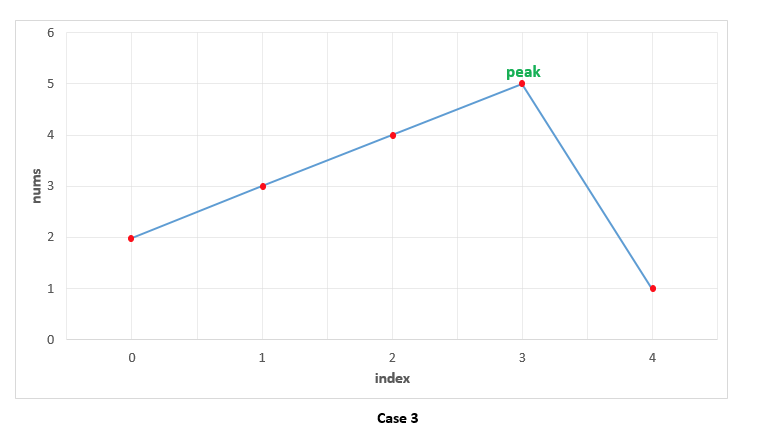
162. 寻找峰值** - 图3

  1. class Solution {
  2. public:
  3.     int findPeakElement(vector<int>& nums) {
  4.         int len = nums.size();
  5.         for(int i=0;i<len-1;i++){
  6.             if(nums[i]>nums[i+1])
  7.                 return i;
  8.         }
  9.         // nums[len-2] <= nums[len-1]
  10.         return len-1;
  11.     }
  12. };
  • 时间复杂度 O(n)
  • 空间复杂度 O(1)

    方法二：递归二分查找

    我们可以将 nums 数组中的任何给定序列视为交替的升序和降序序列。通过利用这一点，以及“可以返回任何一个峰作为结果”的要求，我们可以利用二分查找来找到所需的峰值元素。

在简单的二分查找中，我们处理的是一个有序数列，并通过在每一步减少搜索空间来找到所需要的数字。在本例中，我们对二分查找进行一点修改。
首先从数组 nums 中找到中间的元素 mid。若该元素恰好位于降序序列或者一个局部下降坡度中（通过将 nums[i] 与右侧比较判断)，则说明峰值会在本元素的左边。于是，我们将搜索空间缩小为 mid 的左边(包括其本身)，并在左侧子数组上重复上述过程。

若该元素恰好位于升序序列或者一个局部上升坡度中（通过将 nums[i] 与右侧比较判断)，则说明峰值会在本元素的右边。于是，我们将搜索空间缩小为 mid 的右边，并在右侧子数组上重复上述过程。

就这样，我们不断地缩小搜索空间，直到搜索空间中只有一个元素，该元素即为峰值元素。

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        return search(nums,0,nums.size()-1);
    }
    int search(vector<int>& nums,int left,int right){
        if(left == right)
            return left;
        int mid = left + (right-left)/2;
        if(nums[mid]>nums[mid+1]){
            return search(nums,left,mid);
        }else{
            return search(nums,mid+1,right);
        }
    }
};
  • 时间复杂度 O(log n)
  • 空间复杂度 O(log n)


方法二：迭代二分查找

将二分查找用迭代写

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int l = 0,r = nums.size()-1;
        while(l<r){
            int mid = l + (r-l)/2;
            if(nums[mid]>nums[mid+1])
                r = mid;
            else
                l = mid+1;
        }
        return l;
    }
};

class Solution {
    public int findPeakElement(int[] nums) {
        return binary(nums,0,nums.length-1);
    }
    private int binary(int[] nums, int left,int right){
        if(right == left){
            return left;
        }
        int mid = left + (right - left)/2;
        if(nums[mid]>nums[mid + 1]){
            return binary(nums, left, mid);
        }else{
            return binary(nums,mid+1,right);
        }
    }
}
  • 时间复杂度 O(log n)
  • 空间复杂度 O(1)