题目链接

LeetCode

题目描述

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入： nums = [5,2,3,1]
输出： [1,2,3,5]

示例 2：

输入： nums = [5,1,1,2,0,0]
输出： [0,0,1,1,2,5]

提示：

  1. 1 <= nums.length <= 50000
  2. -50000 <= nums[i] <= 50000

    解题思路

    image.png

    方法一：归并排序

  1. class Solution {
  2.     public int[] sortArray(int[] nums) {
  3.         binarySort(nums, 0, nums.length - 1);
  4.         return nums;
  5.     }
  6.     private void binarySort(int[] nums, int left, int right){
  7.         if(left >= right){
  8.             return;
  9.         }
  10.         int mid = left + (right - left)/2;
  11.         binarySort(nums, left, mid);
  12.         binarySort(nums, mid+1, right);
  13.         int pos = 0, l = left, r= mid + 1;
  14.         int[] result = new int[right - left + 1];
  15.         while(l <= mid && r <= right){
  16.             result[pos++] = nums[l] > nums[r] ? nums[r++] : nums[l++];
  17.         }
  18.         while(l <= mid){
  19.             result[pos++] = nums[l++];
  20.         }
  21.         while(r <= right){
  22.             result[pos++] = nums[r++];
  23.         }
  25.         for(int i = 0; left <= right; ++i){
  26.             nums[left++] = result[i];
  27.         }
  28.     }
  29. }
  • 时间复杂度 O(n log n)
  • 空间复杂度 O(n)

    方法二：快排

  1. class Solution {
  2.     Random r = new Random();
  3.     public int[] sortArray(int[] nums) {
  4.         quickSort(nums, 0, nums.length-1);
  5.         return nums;
  6.     }
  7.     private void quickSort(int[] nums, int left, int right){
  8.         if(left >= right){
  9.             return;
  10.         }
  11.         // 随机选取基数点
  12.         swap(nums, left, r.nextInt(right - left) + left);
  13.         // 记录基数值
  14.         int num = nums[left];
  15.         // 记录 起始下标
  16.         int l = left, r = right;
  17.         while(left < right){
  18.             while(left < right && nums[right] >= num){
  19.                 --right;
  20.             }
  21.             // 找到小于 基数的值 移到左边
  22.             if(left < right)
  23.                 nums[left++] = nums[right];
  24.             while(left < right && nums[left] <= num){
  25.                 ++left;
  26.             }
  27.             // 找到大于 基数的值 移到右边
  28.             if(left < right)
  29.                 nums[right--] = nums[left];
  30.         }
  31.         // 中间位置放基数值  左边小于等于基数值  右边大于等于基数值
  32.         nums[left] = num;
  33.         // 排序 左右两边
  34.         quickSort(nums, l, left - 1);
  35.         quickSort(nums, left + 1, r);
  36.     }
  37.     private void swap(int nums[], int left, int right){
  38.         int tmp = nums[left];
  39.         nums[left] = nums[right];
  40.         nums[right] = tmp;
  41.     }
  42. }
// 单独记录基数下标
class Solution {
    Random r = new Random();
    public int[] sortArray(int[] nums) {
        quickSort(nums, 0, nums.length-1);
        return nums;
    }
    private void quickSort(int[] nums, int left, int right){
        if(left >= right){
            return;
        }
        swap(nums, left, r.nextInt(right - left) + left);
        int num = nums[left];
        int l = left, r = right;
        int pos = left;
        while(left < right){
            while(left < right && nums[right] >= num){
                --right;
            }
            nums[pos] = nums[right];
            pos = right;
            while(left < right && nums[left] <= num){
                ++left;
            }
            nums[pos] = nums[left];
            pos = left;
        }
        nums[pos] = num;
        quickSort(nums, l, pos - 1);
        quickSort(nums, pos + 1, r);
    }
    private void swap(int nums[], int left, int right){
        int tmp = nums[left];
        nums[left] = nums[right];
        nums[right] = tmp;
    }
}
  • 时间复杂度 O(n log n)
  • 空间复杂度 O(1)

    方法三：堆排序

1、首先了解堆是什么

堆是一种数据结构，一种叫做完全二叉树的数据结构。

2、堆的性质

这里我们用到两种堆，其实也算是一种。
大顶堆：每个节点的值都大于或者等于它的左右子节点的值。
小顶堆：每个节点的值都小于或者等于它的左右子节点的值。

912. 排序数组** - 图2

如上所示，就是两种堆。
如果我们把这种逻辑结构映射到数组中，就是下边这样

| 9 | 5 | 8 | 2 | 3 | 4 | 7 | 1 |

| 1 | 3 | 5 | 4 | 2 | 8 | 9 | 7 |

这个数组arr逻辑上就是一个堆。
从这里我们可以得出以下性质（重点）
对于大顶堆：arr[i] >= arr[2i + 1] && arr[i] >= arr[2i + 2]
对于小顶堆：arr[i] <= arr[2i + 1] && arr[i] <= arr[2i + 2]

3、堆排序的基本思想

了解了以上内容，我们可以开始探究堆排序的基本思想了。

堆排序的基本思想是：1、将带排序的序列构造成一个大顶堆，根据大顶堆的性质，当前堆的根节点（堆顶）就是序列中最大的元素；2、将堆顶元素和最后一个元素交换，然后将剩下的节点重新构造成一个大顶堆；3、重复步骤 2，如此反复，从第一次构建大顶堆开始，每一次构建，我们都能获得一个序列的最大值，然后把它放到大顶堆的尾部。最后，就得到一个有序的序列了。

假设给定的无序序列arr是：

| 4 | 5 | 8 | 2 | 3 | 9 | 7 | 1 |

1、将无序序列构建成一个大顶堆。

首先我们将现在的无序序列看成一个堆结构，一个没有规则的二叉树，将序列里的值按照从上往下，从左到右依次填充到二叉树中。

912. 排序数组** - 图3

根据大顶堆的性质，每个节点的值都大于或者等于它的左右子节点的值。所以我们需要找到所有包含子节点的节点，也就是非叶子节点，然后调整他们的父子关系，非叶子节点遍历的顺序应该是从下往上，这比从上往下的顺序遍历次数少很多，因为，大顶堆的性质要求父节点的值要大于或者等于子节点的值，如果从上往下遍历，当某个节点即是父节点又是子节点并且它的子节点仍然有子节点的时候，因为子节点还没有遍历到，所以子节点不符合大顶堆性质，当子节点调整后，必然会影响其父节点需要二次调整。但是从下往上的方式不需要考虑父节点，因为当前节点调整完之后，当前节点必然比它的所有子节点都大，所以，只会影响到子节点二次调整。相比之下，从下往上的遍历方式比从上往下的方式少了父节点的二次调整。

那么，该如何知道最后一个非叶子节点的位置，也就是索引值？

对于一个完全二叉树，在填满的情况下（非叶子节点都有两个子节点），每一层的元素个数是上一层的二倍，根节点数量是1，所以最后一层的节点数量，一定是之前所有层节点总数+1，所以，我们能找到最后一层的第一个节点的索引，即节点总数/2（根节点索引为0），这也就是第一个叶子节点，所以第一个非叶子节点的索引就是第一个叶子结点的索引-1。那么对于填不满的二叉树呢？这个计算方式仍然适用，当我们从上往下，从左往右填充二叉树的过程中，第一个叶子节点，一定是序列长度/2，所以第一个非叶子节点的索引就是arr.length / 2 -1。

现在找到了最后一个非叶子节点，即元素值为2的节点，比较它的左右节点的值，是否比他大，如果大就换位置。这里因为1<2，所以，不需要任何操作，继续比较下一个，即元素值为8的节点，它的左节点值为9比它本身大，所以需要交换

912. 排序数组** - 图4

交换后的序列为：

| 4 | 5 | 9 | 2 | 3 | 8 | 7 | 1 |

因为元素8没有子节点，所以继续比较下一个非叶子节点，元素值为5的节点，它的两个子节点值都比本身小，不需要调整；然后是元素值为4的节点，也就是根节点，因为9>4，所以需要调整位置

912. 排序数组** - 图5

交换后的序列为：

| 9 | 5 | 4 | 2 | 3 | 8 | 7 | 1 |

此时，原来元素值为9的节点值变成4了，而且它本身有两个子节点，所以，这时需要再次调整该节点

912. 排序数组** - 图6

交换后的序列为：

| 9 | 5 | 8 | 2 | 3 | 4 | 7 | 1 |

到此，大顶堆就构建完毕了。满足大顶堆的性质。

2、排序序列，将堆顶的元素值和尾部的元素交换

912. 排序数组** - 图7

交换后的序列为：

| 1 | 5 | 8 | 2 | 3 | 4 | 7 | 9 |

然后将剩余的元素重新构建大顶堆，其实就是调整根节点以及其调整后影响的子节点，因为其他节点之前已经满足大顶堆性质。

912. 排序数组** - 图8

交换后的序列为：

| 8 | 5 | 7 | 2 | 3 | 4 | 1 | 9 |

然后，继续交换，堆顶节点元素值为8与当前尾部节点元素值为1的进行交换

912. 排序数组** - 图9

交换后的序列为：

| 1 | 5 | 7 | 2 | 3 | 4 | 8 | 9 |

重新构建大顶堆

912. 排序数组** - 图10

交换后的序列为：

| 7 | 5 | 4 | 2 | 3 | 1 | 8 | 9 |

继续交换

912. 排序数组** - 图11

交换后的序列为：

| 1 | 5 | 4 | 2 | 3 | 7 | 8 | 9 |

重新构建大顶堆

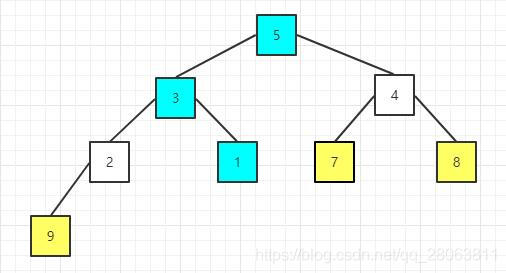
912. 排序数组** - 图12

构建后的序列为：

| 5 | 3 | 4 | 2 | 1 | 7 | 8 | 9 |

继续交换

912. 排序数组** - 图13

交换后的序列为：

| 1 | 3 | 4 | 2 | 5 | 7 | 8 | 9 |

重新构建大顶堆

912. 排序数组** - 图14

构建后的序列为：

| 4 | 3 | 1 | 2 | 5 | 7 | 8 | 9 |

继续交换

912. 排序数组** - 图15

交换后的序列为：

| 2 | 3 | 1 | 4 | 5 | 7 | 8 | 9 |

重新构建大顶堆

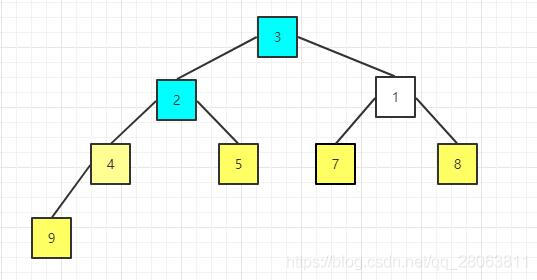
912. 排序数组** - 图16

构建后的序列为：

| 3 | 2 | 1 | 4 | 5 | 7 | 8 | 9 |

继续交换

912. 排序数组** - 图17

交换后的序列为：

| 1 | 2 | 3 | 4 | 5 | 7 | 8 | 9 |

重新构建大顶堆

912. 排序数组** - 图18

构建后的序列为：

| 2 | 1 | 3 | 4 | 5 | 7 | 8 | 9 |

继续交换

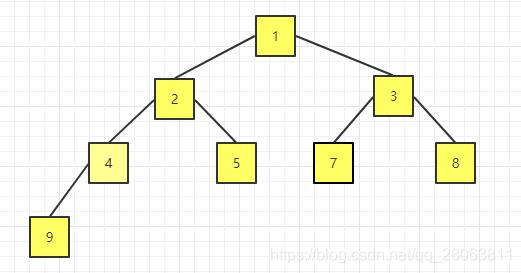
912. 排序数组** - 图19

交换后的序列为：

| 1 | 2 | 3 | 4 | 5 | 7 | 8 | 9 |

此时，序列排序完成。以上就是整个堆排序的逻辑。

class Solution {
    public int[] sortArray(int[] nums) {
        sortHeap(nums);
        return nums;
    }
    // 堆排序的方法如下，把最大堆堆顶的最大数取出，将剩余的堆继续调整为最大堆，
    // 再次将堆顶的最大数取出，这个过程持续到剩余数只有一个时结束。
    private void sortHeap(int[] nums){
        // 从下向上构建大顶堆
        for(int i = nums.length/2 - 1; i >= 0; --i){
            buildMaxHeap(nums, nums.length, i);
        }
        // 将每次的最大值移到当前大顶堆的最后，重建大顶堆
        for(int i = nums.length - 1; i >= 0; --i){
            swap(nums, 0, i);
            buildMaxHeap(nums, i, 0);
        }
    }
    // 最大堆中的最大元素值出现在根结点（堆顶）
    // 堆中每个父节点的元素值都大于等于其孩子结点
    private void buildMaxHeap(int[] nums, int len, int i){
        int lengest = i;
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        if(left < len && nums[left] > nums[lengest]){
            lengest = left;
        }
        if(right < len && nums[right] > nums[lengest]){
            lengest = right;
        }
        if(i != lengest){
            // 设置堆顶最大
            swap(nums, i, lengest);
            // 递归地定义子堆
            buildMaxHeap(nums, len, lengest);
        }
    }
    private void swap(int[] nums, int x, int y){
        int tmp = nums[x];
        nums[x] = nums[y];
        nums[y] = tmp;
    }
}
  • 时间复杂度 O(n log n)
  • 空间复杂度 O(1)