题目链接

题目描述

示例 1：

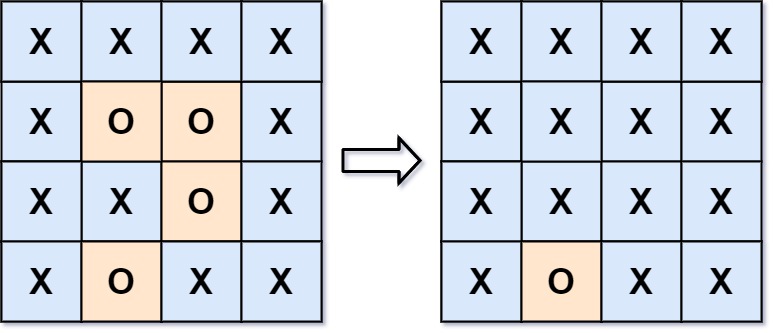
130. 被围绕的区域** - 图1

输入： board = [[“X”,”X”,”X”,”X”],[“X”,”O”,”O”,”X”],[“X”,”X”,”O”,”X”],[“X”,”O”,”X”,”X”]]
输出： [[“X”,”X”,”X”,”X”],[“X”,”X”,”X”,”X”],[“X”,”X”,”X”,”X”],[“X”,”O”,”X”,”X”]]
解释： 被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是 “相连” 的。

示例 2：

输入： board = [[“X”]]
输出： [[“X”]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 'X' 或 'O'

解题思路

方法一：DFS
本题给定的矩阵中有三种元素：
字母 X；
被字母 X 包围的字母 O；
没有被字母 X 包围的字母 O。

本题要求将所有被字母 X 包围的字母 O都变为字母 X ，但很难判断哪些 O 是被包围的，哪些 O 不是被包围的。

注意到题目解释中提到：任何边界上的 **O** 都不会被填充为 **X**。我们可以想到，所有的不被包围的 O 都直接或间接与边界上的 O 相连。我们可以利用这个性质判断 O 是否在边界上，具体地说：

对于每一个边界上的 O，我们以它为起点，标记所有与它直接或间接相连的字母 O；

最后我们遍历这个矩阵，对于每一个字母：

如果该字母被标记过，则该字母为没有被字母 X 包围的字母 O，我们将其还原为字母 O；

如果该字母没有被标记过，则该字母为被字母 X 包围的字母 O，我们将其修改为字母 X。

class Solution {
public void solve(char[][] board) {
   int n = board.length;
   if(n == 0){
       return;
   }
   // 左右边界向内遍历
   int m = board[0].length;
   for(int i = 0; i < n; ++i){
       dfs(board, i, 0);
       dfs(board, i, m - 1);
   }
   // 上下边界向内遍历
   for(int i = 0; i < m; ++i){
       dfs(board, 0, i);
       dfs(board, n - 1, i);
   }
   // 将剩余的 'O' 转换为 'X'，将 'A'（与边界连接的'O'） 转换为'O'
   for(int i = 0; i < n; ++i){
       for(int j = 0; j < m; ++j){
           if(board[i][j] == 'A'){
               board[i][j] = 'O';
           }else if(board[i][j] == 'O'){
               board[i][j] = 'X';
           }
       }
   }
}
// 深度优先遍历，与边界相连的 'O'字符用 'A' 表示
private void dfs(char[][] board, int i, int j){
   if(i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] != 'O'){
       return;
   }
   board[i][j] = 'A';
   dfs(board, i - 1, j);
   dfs(board, i + 1, j);
   dfs(board, i, j - 1);
   dfs(board, i, j + 1);
}
}

时间复杂度 O(n * m)
空间复杂度 O(n * m)
方法二：BFS

class Solution {
    int[] x = new int[]{-1, 1, 0, 0};
    int[] y = new int[]{0, 0, -1, 1};
    public void solve(char[][] board) {
        int n = board.length;
        if(n == 0){
            return;
        }
        Deque<int[]> q = new LinkedList<>();
        // 左右边界向内遍历
        int m = board[0].length;
        for(int i = 0; i < n; ++i){
            if(board[i][0] == 'O'){
                board[i][0] = 'A';
                q.offer(new int[]{i, 0});
            }
            if(board[i][m - 1] == 'O'){
                board[i][m - 1] = 'A';
                q.offer(new int[]{i, m - 1});
            }
        }
        // 上下边界向内遍历
        for(int i = 0; i < m; ++i){
            if(board[0][i] == 'O'){
                board[0][i] = 'A';
                q.offer(new int[]{0, i});
            }
            if(board[n - 1][i] == 'O'){
                board[n - 1][i] = 'A';
                q.offer(new int[]{n - 1, i});
            }
        }
        while(!q.isEmpty()){
            int[] tmp = q.poll();
            for(int i = 0; i < 4; ++i){
                if(tmp[0] + x[i] >= 0 && tmp[0] + x[i] < n && tmp[1] + y[i] >= 0 && tmp[1] + y[i] < m && board[tmp[0] + x[i]][tmp[1] + y[i]] == 'O'){
                    board[tmp[0] + x[i]][tmp[1] + y[i]] = 'A';
                    q.offer(new int[]{tmp[0] + x[i], tmp[1] + y[i]});
                }
            }
        }
        // 将剩余的 'O' 转换为 'X'，将 'A'（与边界连接的'O'） 转换为'O'
        for(int i = 0; i < n; ++i){
            for(int j = 0; j < m; ++j){
                if(board[i][j] == 'A'){
                    board[i][j] = 'O';
                }else if(board[i][j] == 'O'){
                    board[i][j] = 'X';
                }
            }
        }
    }
}

时间复杂度 O(n * m)
空间复杂度 O(n * m)

130. 被围绕的区域**

题目链接

题目描述

解题思路

方法一：DFS

方法二：BFS