题目链接

LeetCode

题目描述

单词数组 words 的 有效编码 由任意助记字符串 s 和下标数组 indices 组成，且满足：

• words.length == indices.length
• 助记字符串 s 以 '#' 字符结尾
• 对于每个下标 indices[i] ，s 的一个从 indices[i] 开始、到下一个 '#' 字符结束（但不包括 '#'）的 子字符串 恰好与 words[i] 相等

给你一个单词数组 words ，返回成功对 words 进行编码的最小助记字符串 s 的长度 。

示例 1：

输入： words = [“time”, “me”, “bell”]
输出： 10
解释： 一组有效编码为 s = "time#bell#" 和 indices = [0, 2, 5] 。
words[0] = “time” ，s 开始于 indices[0] = 0 到下一个 ‘#’ 结束的子字符串，如加粗部分所示 “time#bell#”
words[1] = “me” ，s 开始于 indices[1] = 2 到下一个 ‘#’ 结束的子字符串，如加粗部分所示 “time#bell#”
words[2] = “bell” ，s 开始于 indices[2] = 5 到下一个 ‘#’ 结束的子字符串，如加粗部分所示 “time#bell#”

示例 2：

输入： words = [“t”]
输出： 2
解释： 一组有效编码为 s = “t#” 和 indices = [0] 。

提示：

• 1 <= words.length <= 2000
• 1 <= words[i].length <= 7

• words[i] 仅由小写字母组成

  解题思路

  方法一：排序 + 前缀树

  思路
  如方法一所说，目标就是保留所有不是其他单词后缀的单词。
  算法
  去找到是否不同的单词具有相同的后缀，我们可以将其反序之后插入字典树中。例如，我们有 “time” 和 “me”，可以将 “emit” 和 “em” 插入字典树中。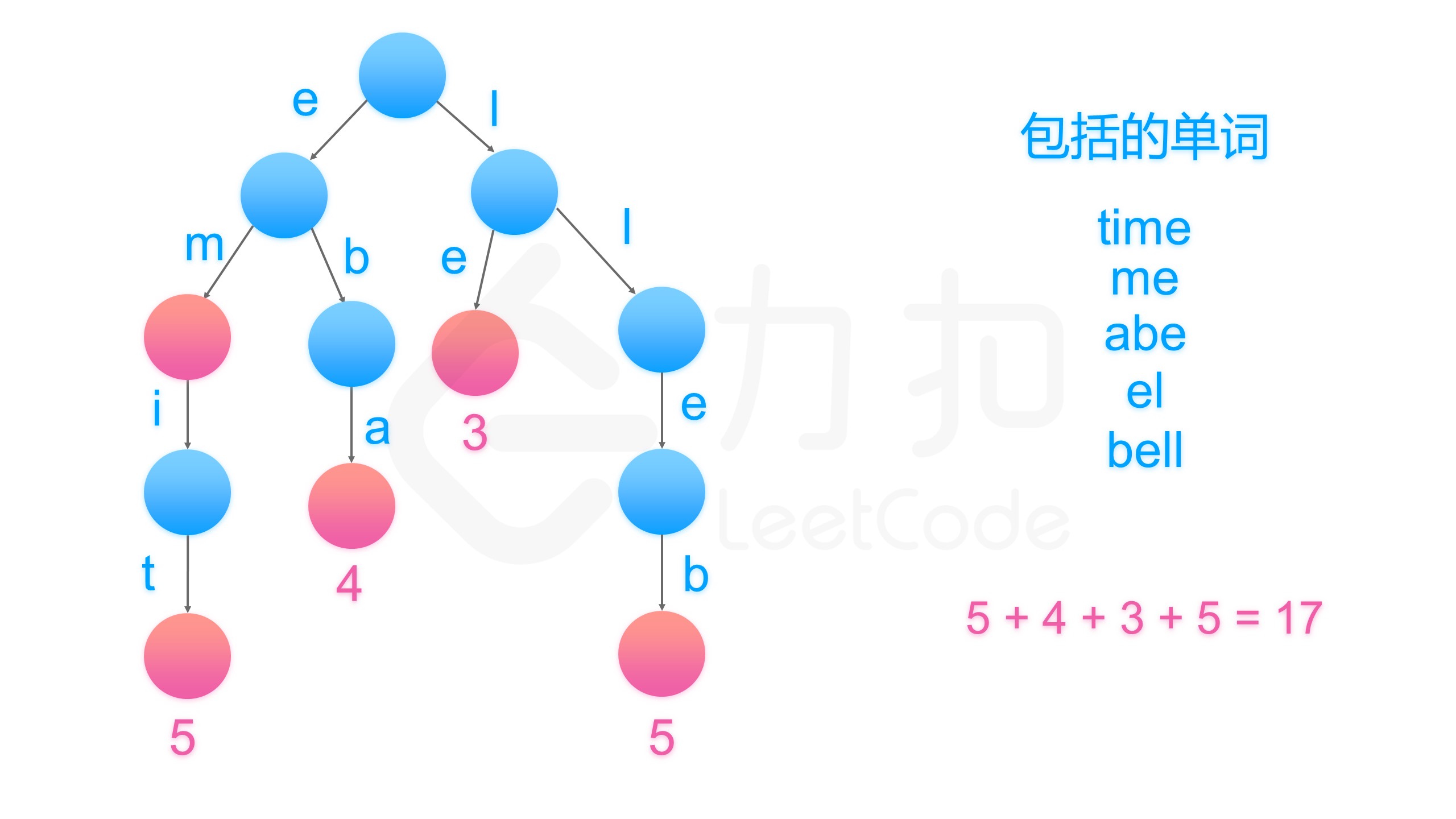
  
  然后，字典树的叶子节点（没有孩子的节点）就代表没有后缀的单词，统计叶子节点代表的单词长度加一的和即为我们要的答案。

  class Solution {
    public int minimumLengthEncoding(String[] words) {
        Trie trie = new Trie();
        Map<Trie, Integer> map = new HashMap<>();
        for(int i = 0; i < words.length; ++i){
            Trie cur = trie;
            // 向下探索
            for(int j = words[i].length() - 1; j >= 0; --j){
                cur = cur.get(words[i].charAt(j));
            }
            // 记录当前单词最后一个节点下一层节点个数
            // 如果下层节点个数为 0，则这是最后一层
            map.put(cur, i);
        }
        int res = 0;
        for(Trie t : map.keySet()){
            // 如果下层节点个数为 0，则这是最后一层
            if(t.count == 0){
                // 单词长度加一个 '#'
                res += words[map.get(t)].length() + 1;
            }
        }
        return res;
    }
  }
  class Trie {
    private Trie[] childen;
    int count;  // 下一层节点个数
    public Trie() {
        childen = new Trie[26];
        count = 0;  // 下一层节点个数默认为 0 
    }
    public Trie get(char c) {
        int index = c - 'a';
        if(childen[index] == null){
            childen[index] = new Trie();
            // 下一层节点个数加一
            ++count;
        }
        return childen[index];
    }
  }

• 时间复杂度 O(n)

• 空间复杂度 O(n)