题目链接

LeetCode

题目描述

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易（即买入和卖出一支股票一次），设计一个算法来计算你所能获取的最大利润。
注意：你不能在买入股票前卖出股票。

解题思路

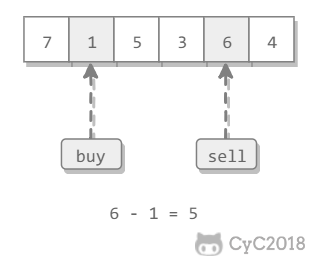
我们需要找出给定数组中两个数字之间的最大差值（即，最大利润）。此外，第二个数字（卖出价格）必须大于第一个数字（买入价格）。
形式上，对于每组 i 和 j（其中 j > i）我们需要找出 max(prices[j]−prices[i])。

方法一：暴力

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = (int)prices.size(), ans = 0;
        for (int i = 0; i < n; ++i){
            for (int j = i + 1; j < n; ++j) {
                ans = max(ans, prices[j] - prices[i]);
            }
        }
        return ans;
    }
};

• 时间复杂度：O(n^2)。

• 空间复杂度：O(1)。

  方法二：小顶堆

  通过小顶堆取得之前的最小值

  class Solution {
  public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if(len<2){
            return 0;
        }
        priority_queue<int,vector<int>,greater<int>> pq;
        pq.push(prices[0]);
        int res = 0;
        for(int i=1;i<len;i++){
            res = max(res,prices[i]-pq.top());
            pq.push(prices[i]);
        }
        return res;
    }
  };

• 时间复杂度：O(n)。

• 空间复杂度：O(n)。

  方法三：贪心

  使用贪心策略，假设第 i 轮进行卖出操作，买入操作价格应该在 i 之前并且价格最低。因此在遍历数组时记录当前最低的买入价格，并且尝试将每个位置都作为卖出价格，取收益最大的即可。

  class Solution {
  public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()==0)
            return 0;
        int minprice = prices[0], maxprofit = 0;
        for (int price: prices) {
            minprice = min(price, minprice); //判断当前价格是否为最低价
            maxprofit = max(maxprofit, price - minprice); //将此前的最大利润比较，得出当前最大利润
        }
        return maxprofit;
    }
  };
  

• 时间复杂度：O(n)。

• 空间复杂度：O(1)。