题目链接

牛客网

题目描述

输入一个字符串，按字典序打印出该字符串中字符的所有排列。例如输入字符串 abc，则打印出由字符 a, b, c 所能排列出来的所有字符串 abc, acb, bac, bca, cab 和 cba。

解题思路

递归DFS+剪枝+回溯

排列方案数量： 对于一个长度为 n 的字符串（假设字符互不重复），其排列共有 n×(n−1)×(n−2)…×2×1 种方案。
排列方案的生成方法： 根据字符串排列的特点，考虑深度优先搜索所有排列方案。即通过字符交换，先固定第 1 位字符（ n 种情况）、再固定第 2 位字符（ n−1 种情况）、… 、最后固定第 n 位字符（ 1 种情况）。

如图：

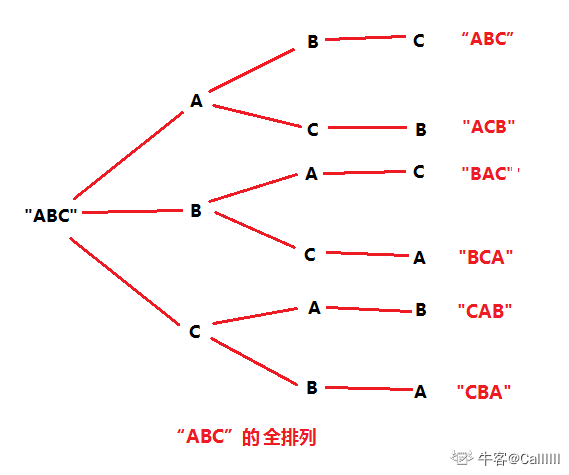
如图所示的全排列可以发现：

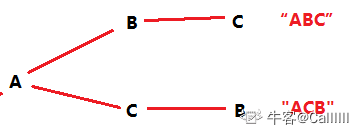
对于这个排列，我们是固定A不动，然后交换B与C，从而得到"ABC" 和 "ACB"
同理，对于"BAC"、"BCA" 、"CAB"和"CBA"是同样道理
递归三部曲：

1. 递归函数的功能：dfs(int pos, string s), 表示固定字符串s的pos下标的字符s[pos]
2. 递归终止条件：当pos+1 == s.length()的时候，终止，表示对最后一个字符进行固定，也就说明，完成了一次全排列
3. 下一次递归：dfs(pos+1, s), 很显然，下一次递归就是对字符串的下一个下标进行固定

但是，对于"ABB"来说，就会有重复，如图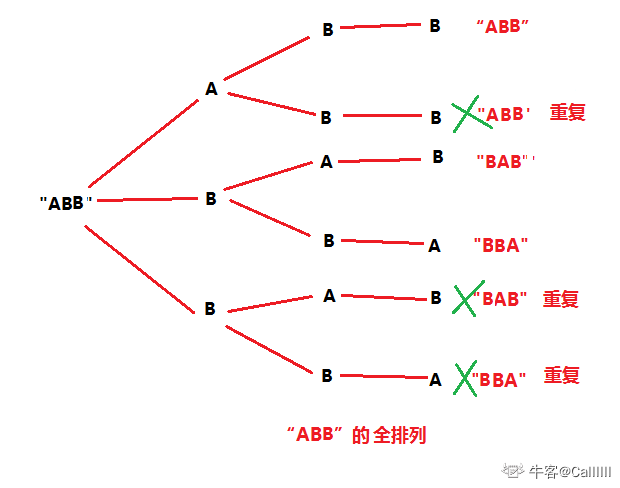

所以，我们用set可以进行去重，并且可以达到按字母顺序排序。

class Solution {
public:
    void perm(int pos, string s, set<string> &ret) {
        if (pos+1 == s.length()) {
            ret.insert(s);
            return;
        }
        // for循环和swap的含义：对于“ABC”，
        // 第一次'A' 与 'A'交换，字符串为"ABC", pos为0， 相当于固定'A'
        // 第二次'A' 与 'B'交换，字符串为"BAC", pos为0， 相当于固定'B'
        // 第三次'A' 与 'C'交换，字符串为"CBA", pos为0， 相当于固定'C'
        for (int i = pos; i < s.length(); ++i) {
            swap(s[pos], s[i]);
            perm(pos+1, s, ret);
            swap(s[pos], s[i]);
            // 回溯的原因：比如第二次交换后是"BAC"，需要回溯到"ABC"
            // 然后进行第三次交换，才能得到"CBA"
        }
    }
    vector<string> Permutation(string s) { 
        if (s.empty()) return {};
        set<string> ret;
        perm(0, s, ret);
        return vector<string>({ret.begin(), ret.end()});
    }
};

• 时间复杂度：O(n!),比如3个字符的全排列有6种
• 空间复杂度：O(1),原地交换