题目链接

牛客网

题目描述

定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的min函数（时间复杂度应为O（1））。

解题思路

方法一：辅助栈

使用一个额外的 minStack，栈顶元素为当前栈中最小的值。在对栈进行 push 入栈和 pop 出栈操作时，同样需要对 minStack 进行入栈出栈操作，从而使 minStack 栈顶元素一直为当前栈中最小的值。
在进行 push 操作时，需要比较入栈元素和当前栈中最小值（当前栈中最小值为minStack的栈顶），将值较小的元素 push 到 minStack 中，让minStack中的每个位置的值都是 原始栈以当前位置为栈顶的最小值。

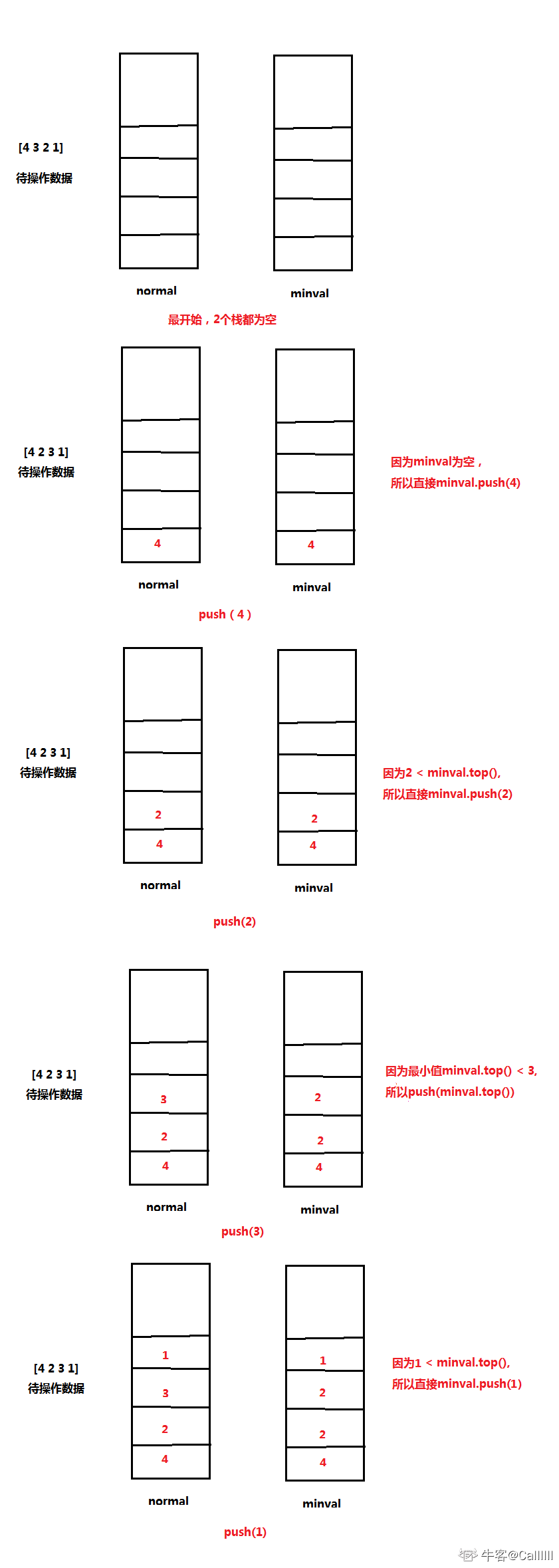
30. 包含 min 函数的栈 - 图1

  1. class Solution {
  2. public:
  3.     stack<int> normal,minval;
  4.     void push(int value) {
  5.         normal.push(value);
  6.         if(minval.empty()){
  7.             minval.push(value);
  8.         }else{
  9.             if(value <= minval.top())
  10.                 minval.push(value);
  11.             else
  12.                 minval.push(minval.top());
  13.         }
  14.     }
  15.     void pop() {
  16.         normal.pop();
  17.         minval.pop();
  18.     }
  19.     int top() {
  20.         return normal.top();
  21.     }
  22.     int min() {
  23.         return minval.top();
  24.     }
  25. };
  1. class MinStack {
  2.     private Stack<Integer> stack;
  3.     private Stack<Integer> min_stack;
  4.     public MinStack() {
  5.         stack = new Stack<>();
  6.         min_stack = new Stack<>();
  7.     }
  8.     public void push(int x) {
  9.         stack.push(x);
  10.         if(min_stack.isEmpty() || x <= min_stack.peek())
  11.             min_stack.push(x);
  12.     }
  13.     public void pop() {
  14.         if(stack.pop().equals(min_stack.peek()))
  15.             min_stack.pop();
  16.     }
  17.     public int top() {
  18.         return stack.peek();
  19.     }
  20.     public int getMin() {
  21.         return min_stack.peek();
  22.     }
  23. }
  • 时间复杂度：push操作为O(1),pop操作为O(1)
  • 空间复杂度：需要stack来存，O(n)

    方法二：栈里保存差值（空间省）

栈中保存 val - min_st 的值，如果当前val - min_st小于0说明val < min_st，将保存val - min_st并将min_st替换为val
但是会有val - min_st越界问题

class MinStack {
public:
    /** initialize your data structure here. */
    MinStack() {

    }

    void push(int val) {

        if(st.empty()){
            st.push(0);
            min_st = val;
        }else{
            long long t = val - min_st;
            if(t<0){
                min_st = val;
            }
            st.push(t);
        }
    }

    void pop() {
        long long t = st.top();
        st.pop();
        if(t<0){
            min_st = min_st - t;
        }
    }

    int top() {
        long long t = st.top();
        if(t<0){
            return min_st - t;
        }
        return min_st + t;
    }

    int getMin() {
        return min_st;
    }
private:
    stack<long long> st;
    long long min_st;
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(val);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->getMin();
 */