题目链接

LeetCode

题目描述

给定一个数组，将数组中的元素向右移动 k个位置，其中 k是非负数。
进阶：

  • 尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
  • 你可以使用空间复杂度为 O(1) 的 原地算法解决这个问题吗？

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5] 向右旋转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入： nums = [-1,-100,3,99], k = 2
输出： [3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]

提示：

  • 1 <= nums.length <= 2 * 104
  • -231 <= nums[i] <= 231 - 1
  • 0 <= k <= 105

    解题思路

    方法一：数组翻转

    该方法基于如下的事实：当我们将数组的元素向右移动 k 次后，尾部 k%n 个元素会移动至数组头部，其余元素向后移动 k%n 个位置。

该方法为数组的翻转：我们可以先将所有元素翻转，这样尾部的 k%n 个元素就被移至数组头部，然后我们再翻转 [0,k%n−1] 区间的元素和 [k%n,n−1] 区间的元素即能得到最后的答案。

我们以 n=7，k=3 为例进行如下展示：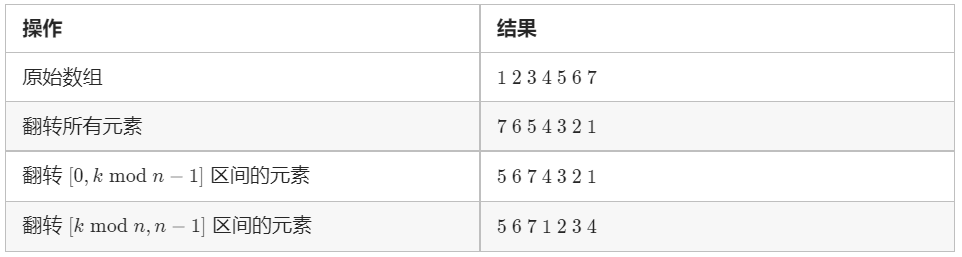
image.png

  1. class Solution {
  2. public:
  3.     void rotate(vector<int>& nums, int k) {
  4.         int len = nums.size();
  5.         if(len<2)
  6.             return;
  7.         k = k%len;
  8.         reverse(nums.begin(),nums.end());
  9.         reverse(nums.begin(),nums.begin()+k);
  10.         reverse(nums.begin()+k,nums.end());
  11.     }
  12. };
  • 时间复杂度 O(n)
  • 空间复杂度 O(1)