题目链接

LeetCode

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。
image.png

解题思路

暴力法（超时）

  1. public class Solution {
  3.     public int reversePairs(int[] nums) {
  4.         int cnt = 0;
  5.         int len = nums.length;
  6.         for (int i = 0; i < len - 1; i++) {
  7.             for (int j = i + 1; j < len; j++) {
  8.                 if (nums[i] > nums[j]) {
  9.                     cnt++;
  10.                 }
  11.             }
  12.         }
  13.         return cnt;
  14.     }
  15. }

时间复制度：O(N^2)

归并排序（分治法）

高级排序算法（快速排序，归并排序）中，能够看到非常明显的阶段排序结果的算法就是归并排序。

预备知识

「归并排序」是分治思想的典型应用，它包含这样三个步骤：

  • 分解： 待排序的区间为 [l, r][l,r]，令 m=⌊(l+r)/2⌋，我们把 [l, r] 分成 [l, m] 和 [m + 1, r]
  • 解决： 使用归并排序递归地排序两个子序列
  • 合并： 把两个已经排好序的子序列 [l, m] 和 [m + 1, r] 合并起来

在待排序序列长度为 11 的时候，递归开始「回升」，因为我们默认长度为 11 的序列是排好序的。

而计算逆序数就发生在排序的过程中，利用了「排序」以后数组的有序性。

  • 关键在于「合并两个有序数组」的步骤，利用数组的部分有序性，一下子计算出一个数之前或者之后元素的逆序的个数；
  • 前面「分」的时候什么都不做，「合」的过程中计算「逆序对」的个数；
  • 「排序」的工作是必要的，正是因为「排序」才能在下一轮利用顺序关系加快逆序数的计算，也能避免重复计算；
  • 在代码实现上，只需要在「归并排序」代码的基础上，加上「逆序对」个数的计算，计算公式需要自己在草稿纸上推导。

下面提供两种写法：
1、在第 2 个子区间元素归并回去的时候，计算逆序对的个数（参考代码 2）；
2、在第 1 个子区间元素归并回去的时候，计算逆序对的个数（参考代码 3）。
注意：两者不能同时计算，否则会计算重复。
参考代码 2：在第 2 个子区间元素归并回去的时候，计算逆序对的个数。

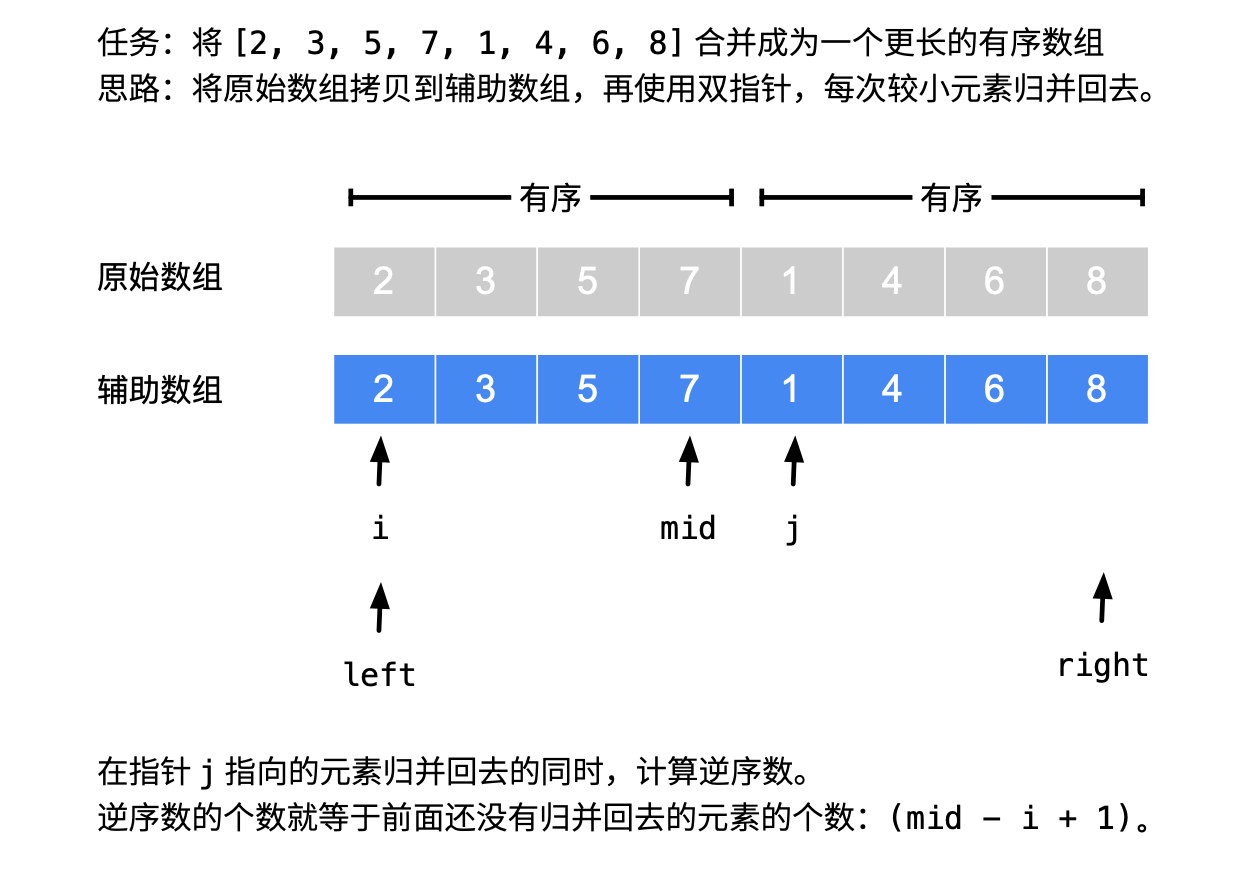
51. 数组中的逆序对* - 图2
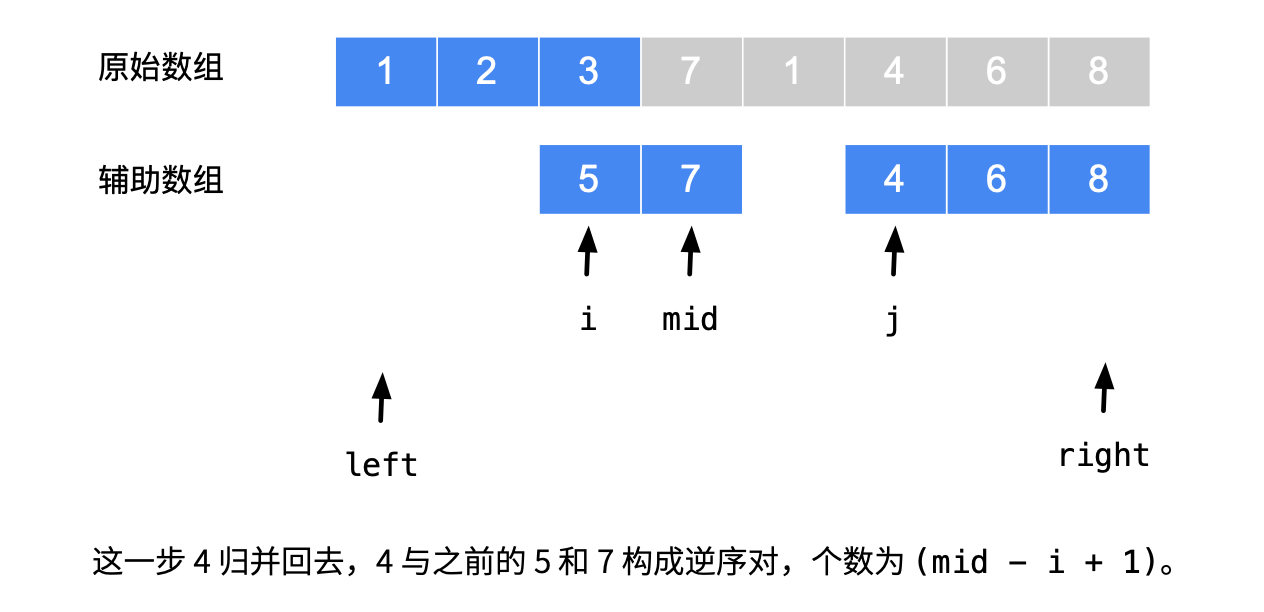
51. 数组中的逆序对* - 图3
即在 j 指向的元素赋值回去的时候，给计数器加上 mid - i + 1。

  1. class Solution {
  2. public:
  3.     int mergeSort(vector<int>& nums, vector<int>& tmp, int l, int r) {
  4.         if(l>=r)
  5.             return 0;
  6.         int mid = l + (r-l)/2; // 避免l和r过大时，l+r溢出
  7.         // 递归计算左右两边
  8.         int inv_count = mergeSort(nums, tmp, l, mid) + mergeSort(nums, tmp, mid + 1, r);
  9.         int i = l,j=mid+1,pos=l;
  10.         while (i <= mid && j <= r) {    // 归并
  11.             if (nums[i] <= nums[j]) {   // 当左边小于等于右边时，插入左边
  12.                 tmp[pos] = nums[i];
  13.                 ++i;
  14.             }
  15.             else {                      // 当右边小于左边时，插入右边，并将逆序数加上左边剩余的元素个数
  16.                 tmp[pos] = nums[j];
  17.                 ++j;
  18.                 inv_count += (mid - i + 1);
  19.             }
  20.             ++pos;
  21.         }
  22.         // 将剩余的元素插入
  23.         for (int k = i; k <= mid; ++k) {
  24.             tmp[pos++] = nums[k];
  25.         }
  26.         for (int k = j; k <= r; ++k) {
  27.             tmp[pos++] = nums[k];
  28.         }
  29.         // 将辅助数组排序好的部分复制给元素数组
  30.         // [ _First，_Last) DestBeg 指出复制到的目标区间起始位置
  31.         // copy(First,Last,DestBeg);
  32.         copy(tmp.begin() + l, tmp.begin() + r + 1, nums.begin() + l);
  33.         // 等同于下面
  34.         // for(int i=l;i<=r;i++){
  35.         //     nums[i]= tmp[i];
  36.         // }
  37.         return inv_count;
  38.     }
  39.     int reversePairs(vector<int>& nums) {
  40.         int n = nums.size();
  41.         if(n<2)
  42.             return 0;
  43.         vector<int> tmp(n); //辅助数组
  44.         return mergeSort(nums, tmp, 0, n - 1);
  45.     }
  46. };
  1. class Solution {
  2.     public int reversePairs(int[] nums) {
  3.         return binarySort(nums, 0, nums.length - 1);
  4.     }
  5.     private int binarySort(int[] nums, int left, int right){
  6.         if(left >= right){
  7.             return 0;
  8.         }
  9.         int res = 0;
  10.         int mid = left + (right - left)/2;
  11.         res += binarySort(nums, left, mid);
  12.         res += binarySort(nums, mid+1, right);
  13.         int[] result = new int[right - left + 1];
  14.         int l = left, r = mid + 1;
  15.         int pos = 0;
  16.         while(l <= mid && r <= right){
  17.             if(nums[r] < nums[l]){
  18.                 result[pos++] = nums[r++];
  19.                 res += (mid - l + 1); 
  20.             }else{
  21.                 result[pos++] = nums[l++];
  22.             }
  23.         }
  24.         while(l <= mid){
  25.             result[pos++] = nums[l++];
  26.         }
  27.         while(r <= right){
  28.             result[pos++] = nums[r++];
  29.         }
  30.         pos = 0;
  31.         for(int i = left; i <= right; ++i){
  32.             nums[i] = result[pos++];
  33.         }
  34.         return res;
  35.     }
  36. }
  • 时间复杂度：O(NlogN): 这里 N 是数组的长度。复杂度是归并排序的时间复杂度，直接看递归树的结点个数或者使用主定理分析，归并的回收每一步计算逆序对的个数是 O(1) 的；
  • 空间复杂度：O(N)。