题目链接

微信公众号

题目描述

一个环上有 length 个点，编号为0-length-1，从0点出发，每步可以顺时针到下一个点，也可以逆时针到上一个点，求：经过n步又回到0点有多少种不同的走法?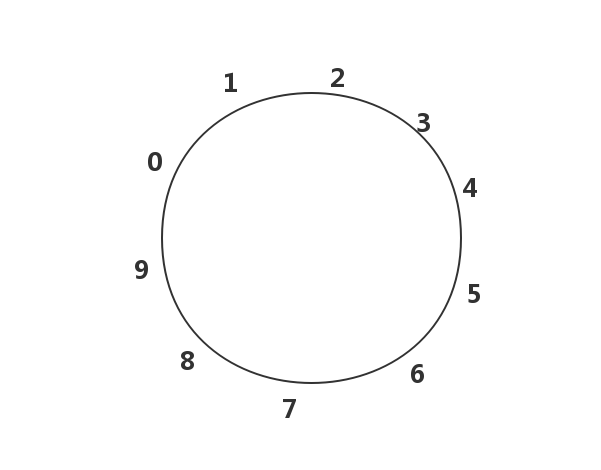
20181226210427162.png

  1. 如果n=1, length=10，则从0出发只能到1或者9，不可能回到0，共0种走法
  2. 如果n=2, length=10，则从0出发有4条路径:0->1->2, 0->1->0, 0->9->8, 0->9->0,其中有两条回到了0点，故一共有2种走法

解题思路

方法一：动态规划

如果你之前做过leetcode的70题爬楼梯，则应该比较容易理解：走n步到0的方案数 = 走n-1步到1的方案数 + 走n-1步到9的方案数。
因此，若设dp[i][j]为从0点出发走 i 步到 j 点的方案数，则递推式为：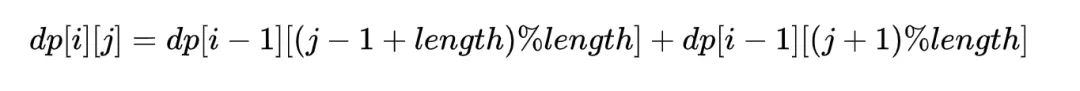
640.webp
ps:公式之所以取余是因为 j - 1 或 j + 1 可能会超过圆环0~9的范围

  1. class Solution {
  2.     public int backToOrigin(int n) {
  3.         // n 走的步数 
  4.         int length = 10;// 点的个数
  5.         int[][] dp = new int[n+1][length];
  6.         dp[0][0] = 1;
  7.         // 走 i 步
  8.         for(int i = 1; i <= n; ++i){
  9.             // 到点 j
  10.             for(int j = 0; j < length; ++j){
  11.                 dp[i][j] = dp[i-1][(j - 1 + length) % length] + dp[i-1][(j + 1) % length];
  12.             }
  13.         }
  14.         return dp[n][0];
  15.     }
  16. }
  • 时间复杂度 O(nm)
  • 空间复杂度 O(nm)