题目链接

LeetCode

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

输入： heights = [2,1,5,6,2,3]
输出： 10
解释： 最大的矩形为图中红色区域，面积为 10

示例 2：

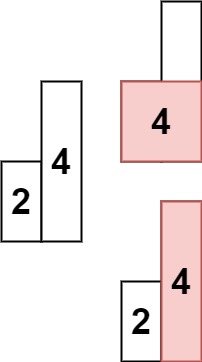
输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=105
• 0 <= heights[i] <= 104

方法一：单调栈

利用单调递增栈，获取每个位置左右两侧小于当前值的位置。也就获得了每个位置的宽度，高为每个位置的值，因为在范围中都是大于等于当前位置值的。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int m = heights.length;
        if(m == 0){
            return 0;
        }
        int res = 0;
        int[] left = new int[m];
        int[] right = new int[m];
        Deque<Integer> stack = new LinkedList<Integer>();
        for(int i = 0; i < m; ++i){
            // 单调递增栈
            // 将大于等于当前高度的弹出
            while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
                stack.pop();
            }
            // left[i] 为左边小于 i 位置值的第一个值下标
            // 如果左边不存在值，则是下标 -1
            left[i] = stack.isEmpty() ? -1 : stack.peek();
            // 输入当前位置
            stack.push(i);
        }
        stack.clear();
        for(int i = m - 1; i >= 0; --i){
            // 单调递增栈
            // 将大于等于当前高度的弹出
            while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
                stack.pop();
            }
            // right[i] 为右边小于 i 位置值的第一个值下标
            // 如果右边不存在值，则是下标 m
            right[i] = stack.isEmpty() ? m : stack.peek();
            // 输入当前位置
            stack.push(i);
        }
        for(int i = 0; i < m; ++i){
            // right[i] - left[i] - 1 为大于等于当前值的范围
            res = Math.max(res, heights[i] * (right[i] - left[i] - 1));
        }
        return res;
    }
}

• 时间复杂度 O(N)
• 空间复杂度 O(N)