题目链接

LeetCode

题目描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

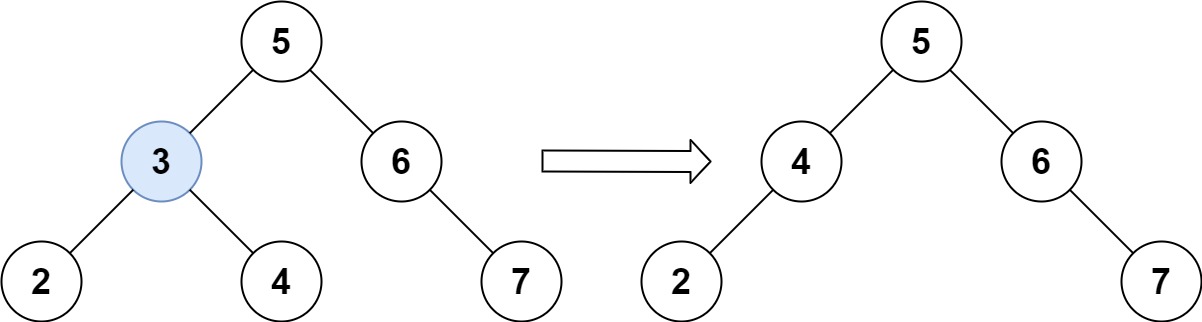
输入： root = [5,3,6,2,4,null,7], key = 3
输出： [5,4,6,2,null,null,7]
解释： 给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
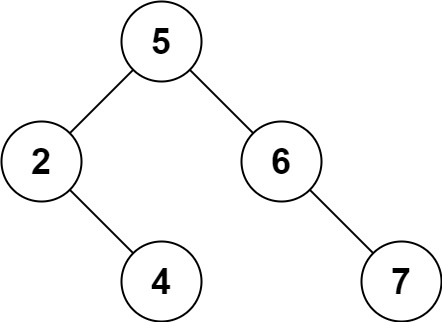
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

• 节点数的范围 [0, 104].
• -105 <= Node.val <= 105
• 节点值唯一
• root 是合法的二叉搜索树
• -105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

解题思路

方法一：递归

根据二叉搜索树的性质

• 如果目标节点大于当前节点值，则去右子树中删除；
• 如果目标节点小于当前节点值，则去左子树中删除；
• 如果目标节点就是当前节点，分为以下三种情况：
  • 其无左子：其右子顶替其位置，删除了该节点；
  • 其无右子：其左子顶替其位置，删除了该节点；
  • 其左右子节点都有：其左子树转移到其右子树的最左节点的左子树上，然后右子树顶替其位置，由此删除了该节点。

第三种情况图示如下：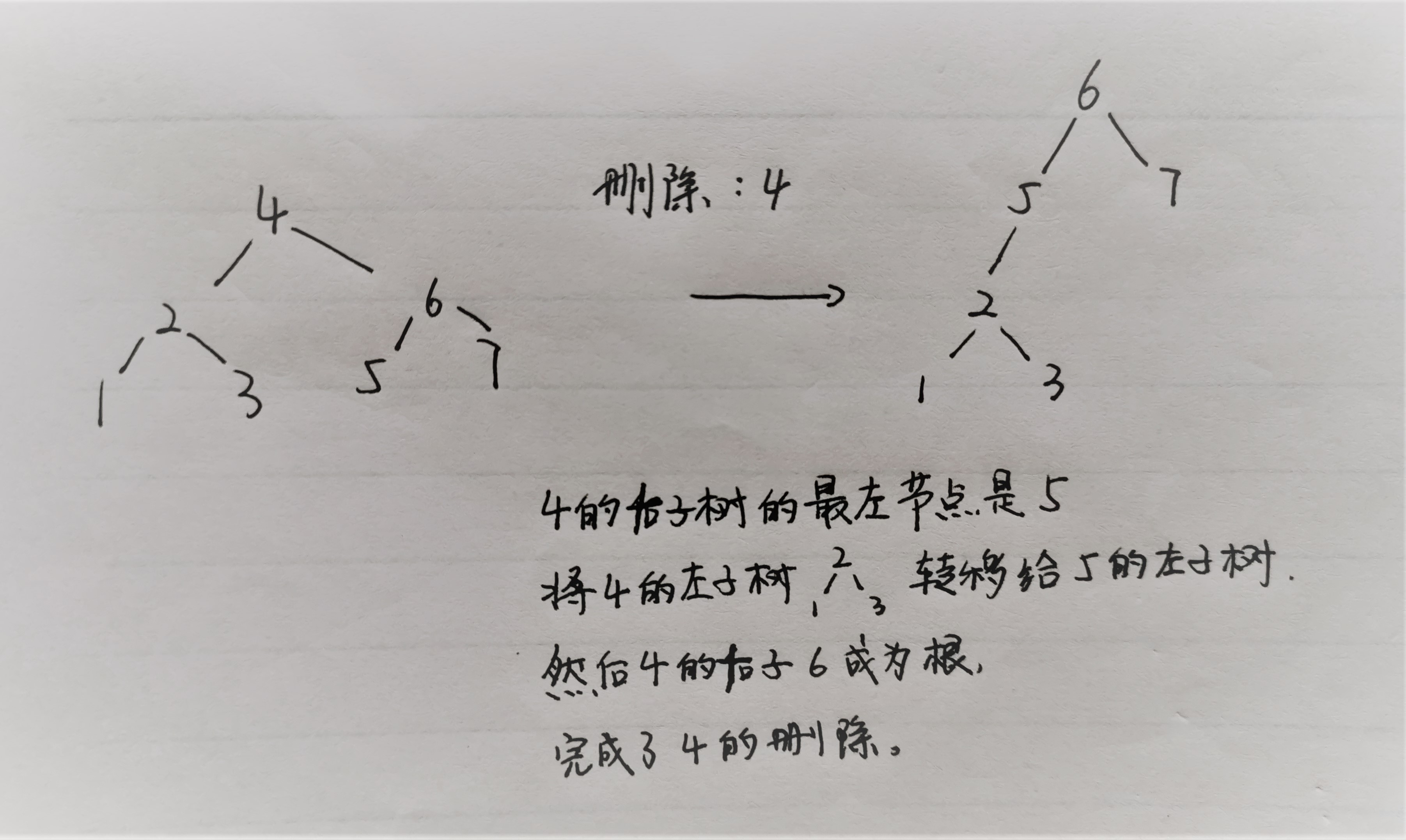

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    TreeNode pre, node;
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root == null){
            return root;
        }
        // 删除节点值大于当前根结点， 所以在左子树，右子树和根节点不变
        if(key > root.val){
            root.right = deleteNode(root.right, key);
        // 删除节点值小于当前根结点， 所以在右子树，左子树和根节点不变
        }else if(key < root.val){
            root.left = deleteNode(root.left, key);
        // 删除节点值等于当前根结点
        }else{
            // 左结点为空， 返回右节点
            if(root.left == null){
                return root.right;
            }
            // 右结点为空， 返回左节点
            if(root.right == null){
                return root.left;
            }
            // 找到右子树的最小值，用于连接当前左子树，保证搜索树性质
            TreeNode node = root.right;
            while(node.left != null){
                node = node.left;
            }
            // 用于连接当前左子树
            node.left = root.left;
            // 删除根节点，利用当前根节点的右子树当根节点
            root = root.right;
        }
        return root;
    }
}

• 时间复杂度 O(H)
• 空间复杂度 O(H)