题目链接

LeetCode

题目描述

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。
子数组为连续的，子序列不连续
示例：

输入：
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出： 3
解释：
长度最长的公共子数组是 [3, 2, 1] 。

提示：

• 1 <= len(A), len(B) <= 1000

• 0 <= A[i], B[i] < 100

  解题思路

  方法一：动态规划

  容易想到一个暴力解法，即枚举数组 A 中的起始位置 i 与数组 B 中的起始位置 j，然后计算 A[i:] 与 B[j:] 的最长公共前缀 k。最终答案即为所有的最长公共前缀的最大值。
  但时间复杂度为O(n^3)
  动态规划：
  dp[i][j]为A[i:]和B[j:]的最长重复子数组。
  令 dp[i][j] 表示 A[i:] 和 B[j:] 的最长公共前缀(即从后向前遍历)，那么答案即为所有 dp[i][j] 中的最大值。如果 A[i] == B[j]，那么 dp[i][j] = dp[i + 1][j + 1] + 1，否则 dp[i][j] = 0。

  class Solution {
  public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int len1 = nums1.size(),len2 = nums2.size();
        if(len1==0||len2==0)
            return 0;
        int ans = 0;
        vector<vector<int>> dp(len1+1,vector<int>(len2+1,0));
        for(int i=len1-1;i>=0;i--){
            for(int j = len2-1;j>=0;j--){
                dp[i][j] = nums1[i] == nums2[j]?dp[i+1][j+1] + 1:0;
                ans = max(ans,dp[i][j]);
            }
        }
        return ans;
    }
  };

  class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int m = nums2.length;
        if(n==0||m==0){
            return 0;
        }
        int[][] dp = new int[n+1][m+1];
        int ans = 0;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(nums1[i] == nums2[j]){
                    dp[i+1][j+1] = dp[i][j]+1;
                    ans = Math.max(ans,dp[i+1][j+1]);
                }
            }
        }
        return ans;
    }
  }
  

• 时间复杂度 O(n*m)

• 空间复杂度 O(n*m)

  方法二：滑动窗口

我们注意到之所以两位置会比较多次，是因为重复子数组在两个数组中的位置可能不同。以 A = [3, 6, 1, 2, 4], B = [7, 1, 2, 9] 为例，它们的最长重复子数组是 [1, 2]，在 A 与 B 中的开始位置不同。
但如果我们知道了开始位置，我们就可以根据它们将 A 和 B 进行「对齐」，即：

A = [3, 6, 1, 2, 4]
B =    [7, 1, 2, 9]

此时，最长重复子数组在A和B中的开始位置相同，我们就可以对这两个数组进行一次遍历，得到子数组的长度，伪代码如下：

ans = 0
len = min(A.length, B.length)
k = 0
for i in [0 .. len - 1] do
    if (A[i] == B[i]) then
        k = k + 1
    else
        k = 0
    end if
    ans = max(ans, k)
end for

我们可以枚举 A 和 B 所有的对齐方式。对齐的方式有两类：第一类为 A 不变，B 的首元素与 A 中的某个元素对齐；第二类为 B 不变，A 的首元素与 B 中的某个元素对齐。对于每一种对齐方式，我们计算它们相对位置相同的重复子数组即可。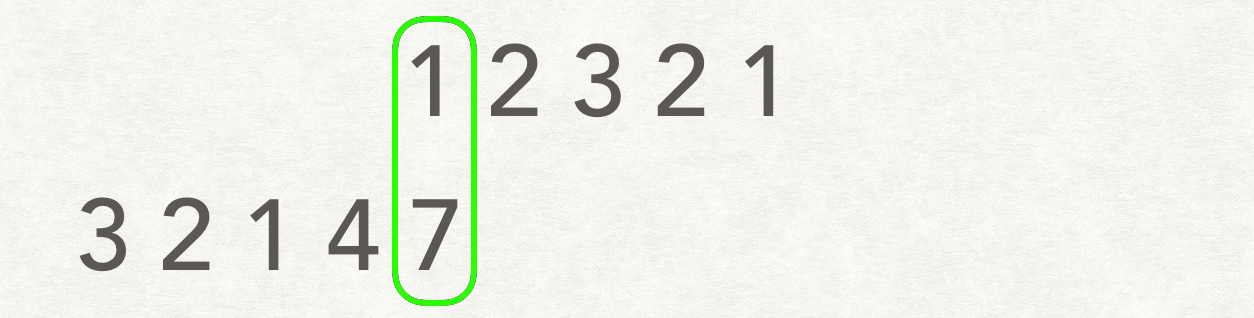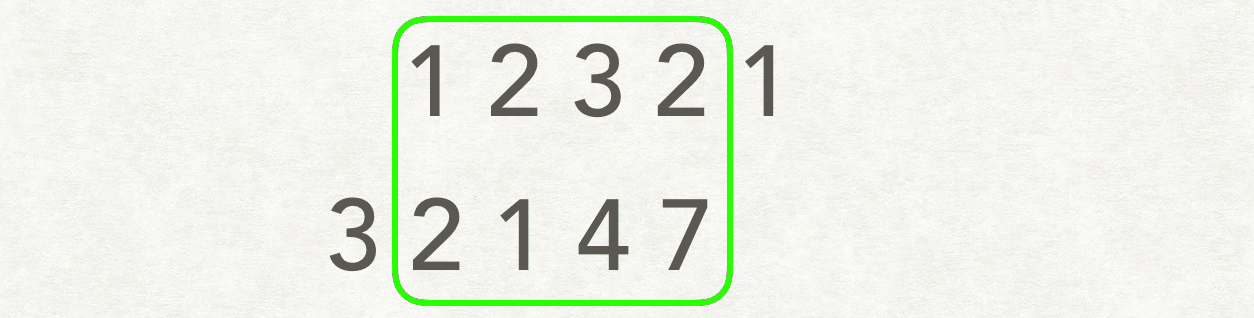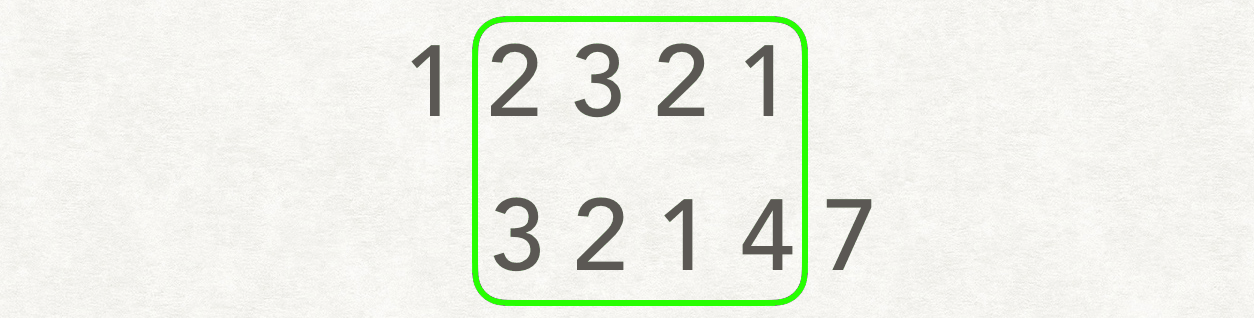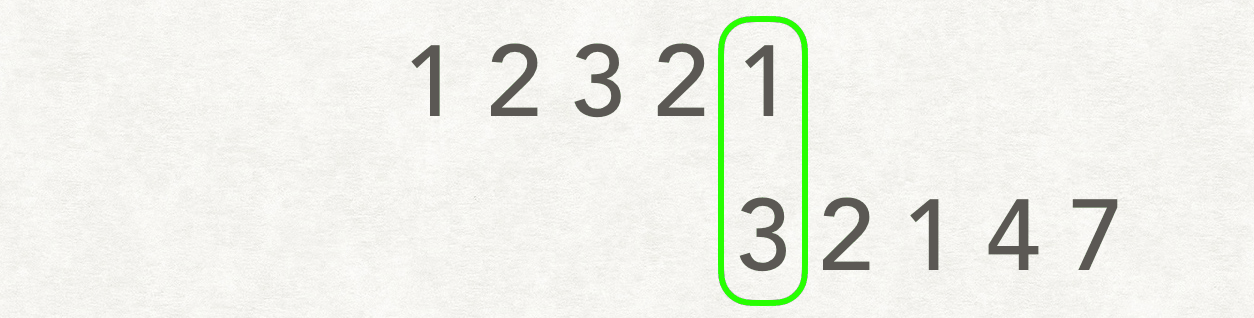

class Solution {
public:
    int maxLength(vector<int>& A, vector<int>& B, int addA, int addB, int len) {
        int ret = 0, k = 0;
        for (int i = 0; i < len; i++) {
            if (A[addA + i] == B[addB + i]) {
                k++;
            } else {
                k = 0;
            }
            ret = max(ret, k);
        }
        return ret;
    }
    int findLength(vector<int>& A, vector<int>& B) {
        int n = A.size(), m = B.size();
        int ret = 0;
        for (int i = 0; i < n; i++) {
            int len = min(m, n - i);
            int maxlen = maxLength(A, B, i, 0, len);
            ret = max(ret, maxlen);
        }
        for (int i = 0; i < m; i++) {
            int len = min(n, m - i);
            int maxlen = maxLength(A, B, 0, i, len);
            ret = max(ret, maxlen);
        }
        return ret;
    }
};

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int m = nums2.length;
        if(n==0||m==0){
            return 0;
        }
        int ans = 0;
        // 相当于 B 不动 A 向左移
        for(int i=0;i<n;i++){
            int len = Math.min(m,n-i);
            ans = Math.max(ans,maxLength(nums1,nums2,i,0,len));
        }
        // 相当于 A 不动 B 向左移
        for(int i=0;i<m;i++){
            int len = Math.min(n,m-i);
            ans = Math.max(ans,maxLength(nums1,nums2,0,i,len));
        }
        return ans;
    }
    private int maxLength(int[] arr1,int[] arr2,int pos1,int pos2,int len){
        int res = 0, k = 0;
        for(int i=0;i<len;i++){
            if(arr1[pos1+i] == arr2[pos2+i]){
                ++k;
            }else{
                res = Math.max(res,k);
                k = 0;
            }
        }
        res = Math.max(res,k);
        return res;
    }
}

• 时间复杂度 O((m+n)*min(m,n))
• 空间复杂度 O(1)