题目链接
题目描述
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
进阶:
- 你可以在
O(n log n)时间复杂度和常数级空间复杂度下,对链表进行排序吗?
示例 1:

输入: head = [4,2,1,3]
输出: [1,2,3,4]
示例 2:

输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]
示例 3:
输入: head = []
输出: []
提示:
- 链表中节点的数目在范围
[0, 5 * 104]内 -
解题思路
方法一:归并排序(递归法,自顶向下)
分割 cut 环节: 找到当前链表中点,并从中点将链表断开(以便在下次递归 cut 时,链表片段拥有正确边界);
- 我们使用 fast,slow 快慢双指针法,奇数个节点找到中点,偶数个节点找到中心左边的节点。
- 找到中点 slow 后,执行 slow.next = None 将链表切断。
- 递归分割时,输入当前链表左端点 head 和中心节点 slow 的下一个节点 tmp(因为链表是从 slow 切断的)。
- cut 递归终止条件: 当head.next == None时,说明只有一个节点了,直接返回此节点。
- 合并 merge 环节: 将两个排序链表合并,转化为一个排序链表。
- 双指针法合并,建立辅助ListNode h 作为头部。
- 设置两指针 left, right 分别指向两链表头部,比较两指针处节点值大小,由小到大加入合并链表头部,指针交替前进,直至添加完两个链表。
- 返回辅助ListNode h 作为头部的下个节点 h.next。
- 时间复杂度 O(l + r),l, r 分别代表两个链表长度。
- 当题目输入的 head == None 时,直接返回None。

/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/class Solution {public:ListNode* sortList(ListNode* head) {return binary_sort(head);}ListNode* binary_sort(ListNode* head){if(head==nullptr||head->next==nullptr){return head;}ListNode*tail = head,*head2 = head;while(head2->next&&head2->next->next){tail = tail->next;head2 = head2->next->next;}head2 = tail->next;tail->next = nullptr;head = binary_sort(head);head2 = binary_sort(head2);return merge_list(head,head2);}ListNode* merge_list(ListNode* head1,ListNode* head2){ListNode* hair = new ListNode();ListNode* cur = hair;while(head1&&head2){if(head1->val<head2->val){cur->next = head1;cur = head1;head1 = head1->next;}else{cur->next = head2;cur = head2;head2 = head2->next;}}if(head1){cur->next = head1;}if(head2){cur->next = head2;}return hair->next;}};
- 时间复杂度 O(nlog n)
空间复杂度 O(log n): 其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间。
方法二:归并排序(自底向上)
对于非递归的归并排序,需要使用迭代的方式替换cut环节:
- 我们知道,cut环节本质上是通过二分法得到链表最小节点单元,再通过多轮合并得到排序结果。
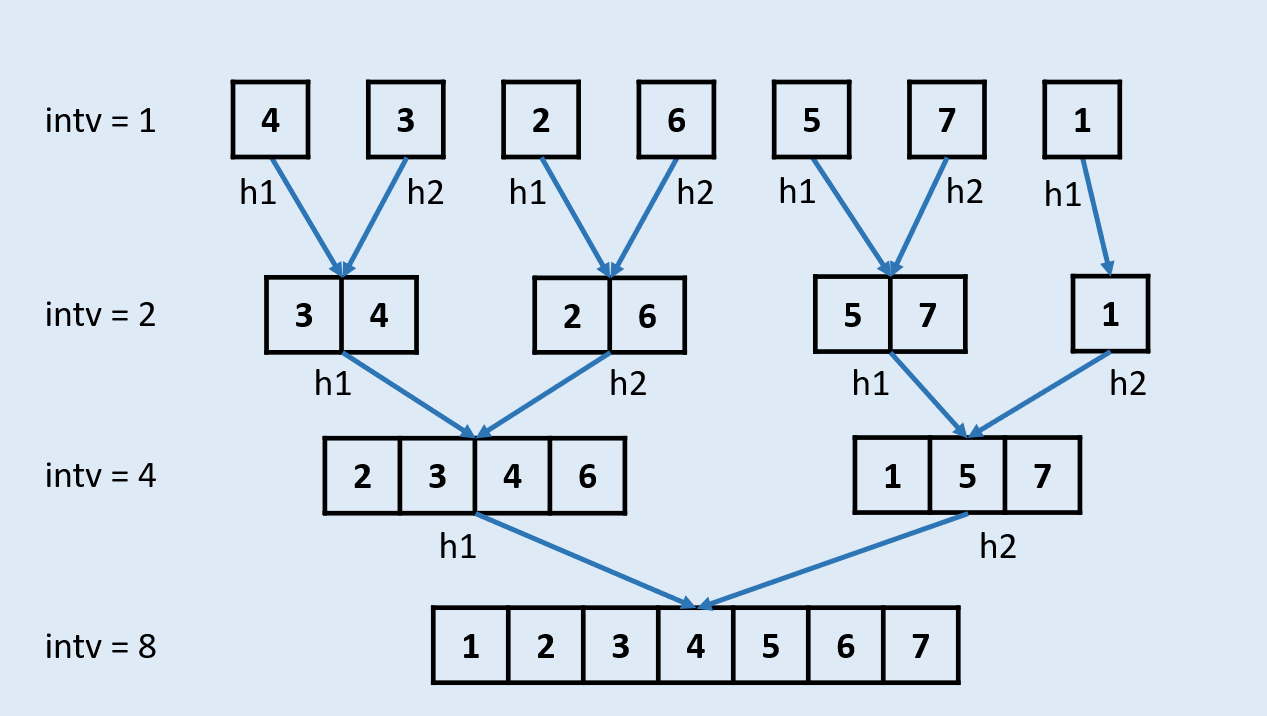
- 每一轮合并merge操作针对的单元都有固定长度intv,例如:
- 第一轮合并时intv = 1,即将整个链表切分为多个长度为1的单元,并按顺序两两排序合并,合并完成的已排序单元长度为2。
- 第二轮合并时intv = 2,即将整个链表切分为多个长度为2的单元,并按顺序两两排序合并,合并完成已排序单元长度为4。
- 以此类推,直到单元长度intv >= 链表长度,代表已经排序完成。
- 根据以上推论,我们可以仅根据intv计算每个单元边界,并完成链表的每轮排序合并,例如:
- 当intv = 1时,将链表第1和第2节点排序合并,第3和第4节点排序合并,……。
- 当intv = 2时,将链表第1-2和第3-4节点排序合并,第5-6和第7-8节点排序合并,……。
- 当intv = 4时,将链表第1-4和第5-8节点排序合并,第9-12和第13-16节点排序合并,……。
- 此方法时间复杂度O(nlogn),空间复杂度O(1)。
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (head == nullptr) {
return head;
}
int length = 0;
ListNode* node = head;
// 1. 首先从头向后遍历,统计链表长度
while (node != nullptr) {
length++;
node = node->next;
}
// 2. 初始化 引入dummyHead
ListNode* dummyHead = new ListNode(0, head);
// 3. 每次将链表拆分成若干个长度为subLen的子链表 , 并按照每两个子链表一组进行合并
for (int subLength = 1; subLength < length; subLength <<= 1) {
// subLen每次左移一位(即sublen = sublen*2) PS:位运算对CPU来说效率更高
ListNode* prev = dummyHead, *curr = dummyHead->next;// curr用于记录拆分链表的位置
while (curr != nullptr) {// 如果链表没有被拆完
// 3.1 拆分subLen长度的链表1
ListNode* head1 = curr;// 第一个链表的头 即 curr初始的位置
// 拆分出长度为subLen的链表1
for (int i = 1; i < subLength && curr->next != nullptr; i++) {
curr = curr->next;
}
// 3.2 拆分subLen长度的链表2
ListNode* head2 = curr->next; // 第二个链表的头 即 链表1尾部的下一个位置
curr->next = nullptr; // 断开第一个链表和第二个链表的链接
curr = head2;// 第二个链表头 重新赋值给curr
// 再拆分出长度为subLen的链表2
for (int i = 1; i < subLength && curr != nullptr && curr->next != nullptr; i++) {
curr = curr->next;
}
// 3.3 再次断开 第二个链表最后的next的链接
ListNode* next = nullptr;
if (curr != nullptr) {
next = curr->next; // next用于记录 拆分完两个链表的结束位置
curr->next = nullptr; // 断开连接
}
// 3.4 合并两个subLen长度的有序链表
ListNode* merged = merge(head1, head2);
prev->next = merged; // prev.next 指向排好序链表的头
// while循环 将prev移动到 subLen*2 的位置后去
while (prev->next != nullptr) {
prev = prev->next;
}
// next用于记录 拆分完两个链表的结束位置
curr = next;
}
}
return dummyHead->next;
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
};
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
if(head==nullptr){
return head;
}
int l = head->val,r = head->val;
double pivot = 0;
// h1表示小于标志值的结点,h2表示大于等于标志值的结点
ListNode* p = head,*q = nullptr,*h1 = nullptr,*h2 = nullptr;
//求最大值和最小值
while(p){
l = min(l,p->val);
r = max(r,p->val);
p = p->next;
}
//如果最大值等于最小值,说明链表值都是相等的
if(l==r){
return head;
}
//取pivot为(最大值+最小值)/2
pivot = (l+r)/2.0;
p = head;
while(p){
q = p->next;//暂存p.next
if(p->val<pivot){//h1代表小于mid的部分 头插法
p->next = h1;
h1 = p;
}else{
p->next = h2;//h2代表大于等于mid的部分 头插法
h2 = p;
}
p =q;// 前移
}
// 递归
h1 = sortList(h1);
h2 = sortList(h2);
// 连接两个链表
p = h1;
while(p->next){
p = p->next;
}
p->next = h2;
return h1;
}
};
- 时间复杂度 O(nlog n)
- 空间复杂度 O(1)

