题目链接

LeetCode

题目描述

给定一个含有 M x N 个元素的矩阵（M 行，N 列），请以对角线遍历的顺序返回这个矩阵中的所有元素，对角线遍历如下图所示。

示例:

输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]

输出: [1,2,4,7,5,3,6,8,9]

解释:
498. 对角线遍历* - 图1

说明:

给定矩阵中的元素总数不会超过 100000 。

解题思路

方法一：模拟法
根据题目描述，首先仔细找一下这道题中一些数字上的规律。

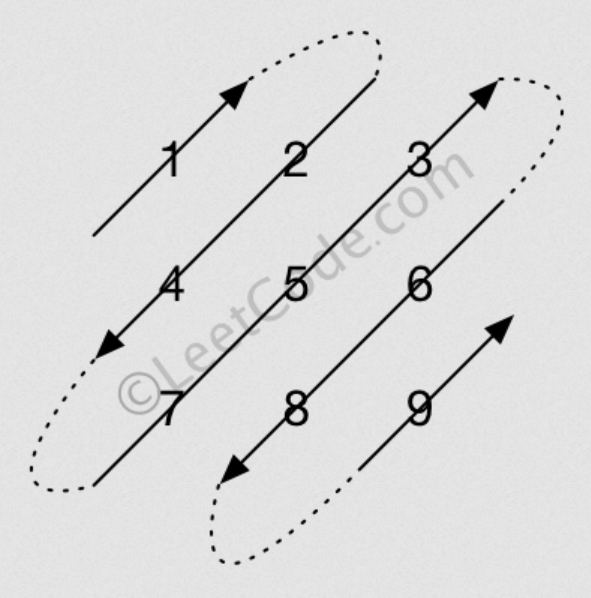
（可以结合题目给的图来看）
得知：
每一趟对角线中元素的坐标（x, y）相加的和是递增的。
- 第一趟：1 的坐标(0, 0)。x + y == 0。
- 第二趟：2 的坐标(1, 0)，4 的坐标(0, 1)。x + y == 1。
- 第三趟：7 的坐标(0, 2), 5 的坐标(1, 1)，3 的坐标(2, 0)。第三趟 x + y == 2。
- 第四趟：……
每一趟都是 x 或 y 其中一个从大到小（每次-1），另一个从小到大（每次+1）。
- 第二趟：2 的坐标(1, 0)，4 的坐标(0, 1)。x 每次-1，y 每次+1。
- 第三趟：7 的坐标(0, 2), 5 的坐标(1, 1)，3 的坐标(2, 0)。x 每次 +1，y 每次 -1。
确定初始值。例如这一趟是 x 从大到小， x 尽量取最大，当初始值超过 x 的上限时，不足的部分加到 y 上面。
- 第二趟：2 的坐标(1, 0)，4 的坐标(0, 1)。x + y == 1，x 初始值取 1，y 取 0。
- 第四趟：6 的坐标(2, 1)，8 的坐标(1, 2)。x + y == 3，x 初始值取 2，剩下的加到 y上，y 取 1。
确定结束值。例如这一趟是 x 从大到小，这一趟结束的判断是， x 减到 0 或者 y 加到上限。
- 第二趟：2 的坐标(1, 0)，4 的坐标(0, 1)。x 减到 0 为止。
- 第四趟：6 的坐标(2, 1)，8 的坐标(1, 2)。x 虽然才减到 1，但是 y 已经加到上限了。

这一趟是 x 从大到小，那么下一趟是 y 从大到小，循环进行。并且方向相反时，逻辑处理是一样的，除了x，y和他们各自的上限值是相反的。

x 从大到小，第二趟：2 的坐标(1, 0)，4 的坐标(0, 1)。x + y == 1，x 初始值取 1，y 取 0。结束值 x 减到 0 为止。

x 从小到大，第三趟：7 的坐标(0, 2)，5 的坐标(1, 1)，3 的坐标(2, 0)。x + y == 2，y 初始值取 2，x 取 0。结束值 y 减到 0 为止。

class Solution {
public:
vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
   vector<int> nums;
   int m = mat.size();
   int n = mat[0].size();
   int i=0;
   while(i<m+n){
       // 确定初始值。例如这一趟是 x 从大到小， x 尽量取最大，当初始值超过 x 的上限时，
       // 不足的部分加到 y 上面。
       // 所以当i大于等于m时，x最大可以取m-1;
       int x1 = (i<m)?i:m-1;
       int y1 = i-x1;
       while(x1>=0&&y1<n){
           nums.push_back(mat[x1][y1]);
           x1--;
           y1++;
       }
       i++;
       if(i>=m+n)
           break;
       int y2 = (i<n)?i:n-1;
       int x2 = i-y2;
       while(y2>=0&&x2<m){
           nums.push_back(mat[x2][y2]);
           x2++;
           y2--;
       }
       i++;
   }
   return nums;
}
};

class Solution {
public int[] findDiagonalOrder(int[][] mat) {
   int[] res = new int[mat.length * mat[0].length];
   int pos = 0, row = mat.length, col = mat[0].length;
   int i = 0, j = 0;// i 是行 j 是列
   while(pos < res.length){
       // 先向上遍历
       while(i >= 0 && j < col){
           res[pos++] = mat[i][j];
           // 向左上移动
           --i;
           ++j;
       }
       // 如果右上角的最后一个元素不在最后一列，从下列这一行开始向下遍历
       if(j < col){
           i = i + 1;
       }else{
       // 如果右上角的最后一个元素是最后一列，从当前列下一行开始向下遍历
           i = i + 2;
           j = j - 1;
       }
       // 再向下遍历
       while(j >= 0 && i < row){
           res[pos++] = mat[i][j];
           // 向右下移动
           ++i;
           --j;
       }
       // 如果右下角的最后一个元素不在最后一行，从下行这一列开始向上遍历
       if(i < row){
           j = j + 1;
       }else{
       // 如果左上角的最后一个元素是最后一行，从当前行下一列开始向下遍历
           i = i - 1;
           j = j + 2;
       }
   }
   return res;
}
}

时间复杂度 O(MN)
空间复杂度 O(1) 返回值空间不算

498. 对角线遍历*

题目链接

题目描述

解题思路

方法一：模拟法