题目链接

LeetCode

题目描述

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入： nums = [10,9,2,5,3,7,101,18]
输出： 4
解释： 最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入： nums = [0,1,0,3,2,3]
输出： 4

示例 3：

输入： nums = [7,7,7,7,7,7,7]
输出： 1

提示：

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

进阶：

• 你可以设计时间复杂度为 O(n2) 的解决方案吗？
• 你能将算法的时间复杂度降低到 O(n log(n)) 吗?

  解题思路

  方法一：动态规划

  

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int len = nums.size();
        if(len<2)
            return len;
        vector<int> dp(len,1);
        int res = 1;
        for(int i=0;i<len;++i){
            for(int j=0;j<i;++j){
                if(nums[j]<nums[i]){
                    dp[i] = max(dp[i],dp[j]+1);
                }
            }
            res = max(dp[i],res);
        }
        return res;
    }
};

class Solution {
    public int lengthOfLIS(int[] nums) {
        if(nums.length == 0){
            return 0;
        }
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        int res = 1;
        for(int i = 0; i < nums.length; ++i){
            for(int j = 0; j < i; ++j){
                if(nums[j] < nums[i]){
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

• 时间复杂度 O(n^2)
• 空间复杂度 O(n)

  方法二：贪心+二分查找

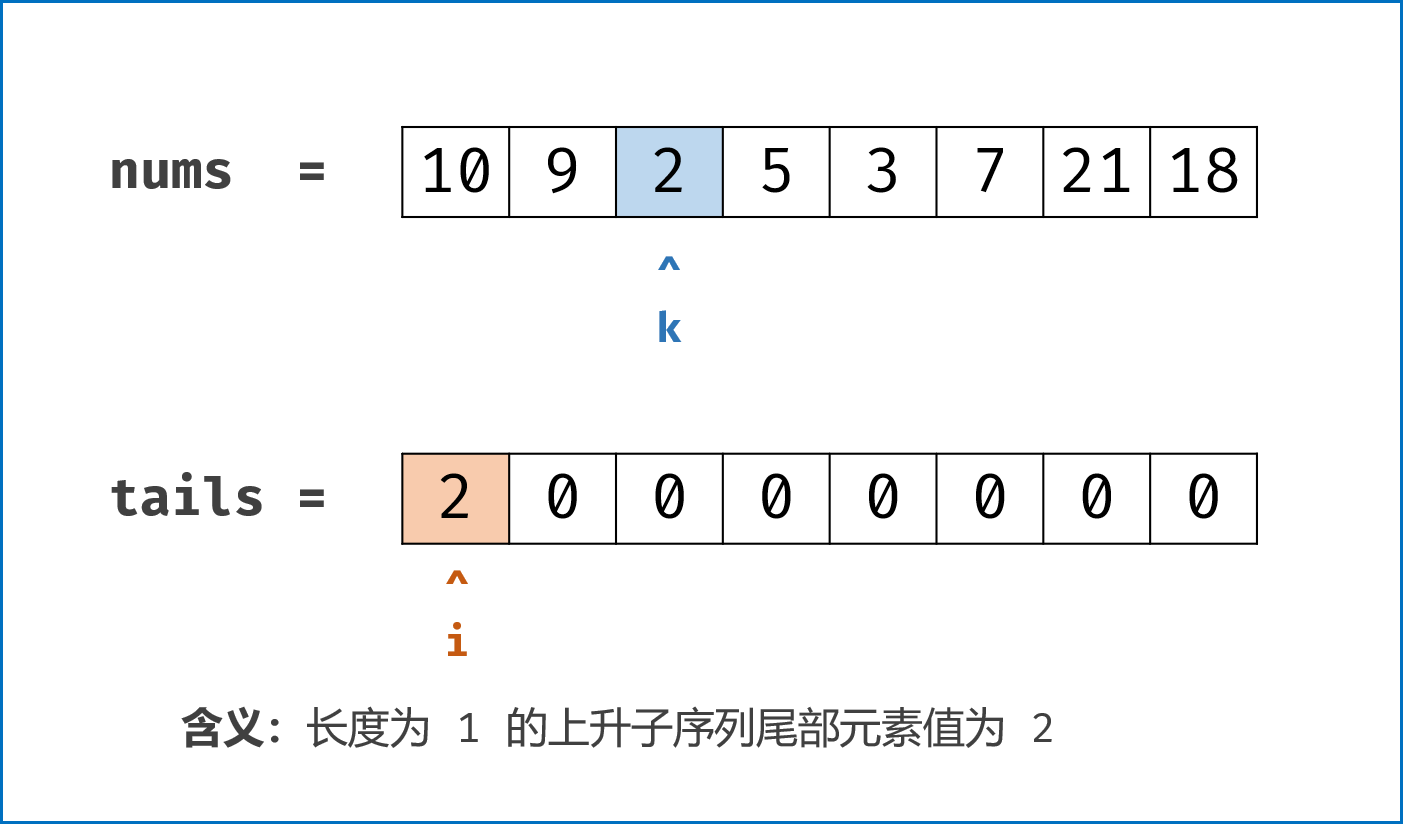
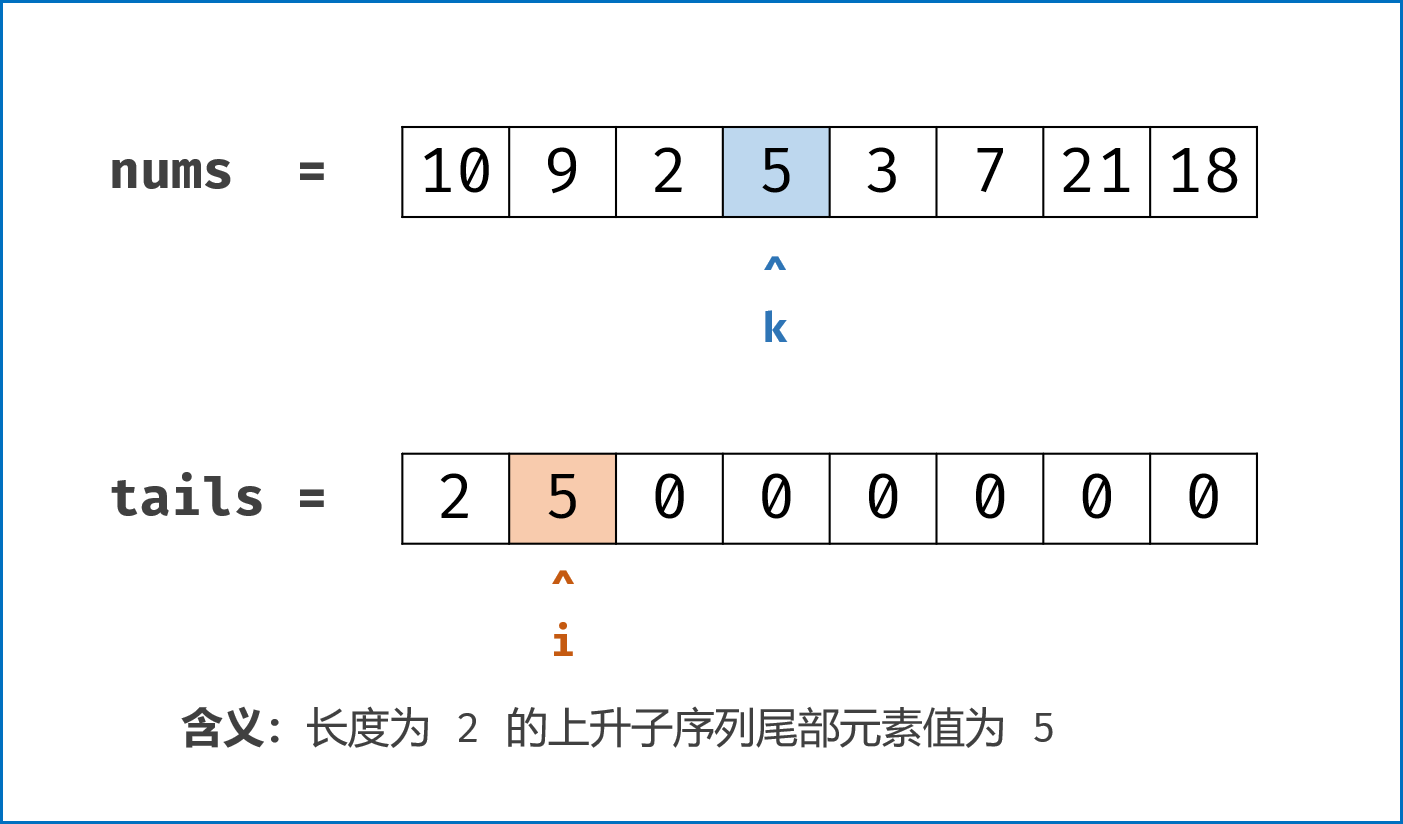
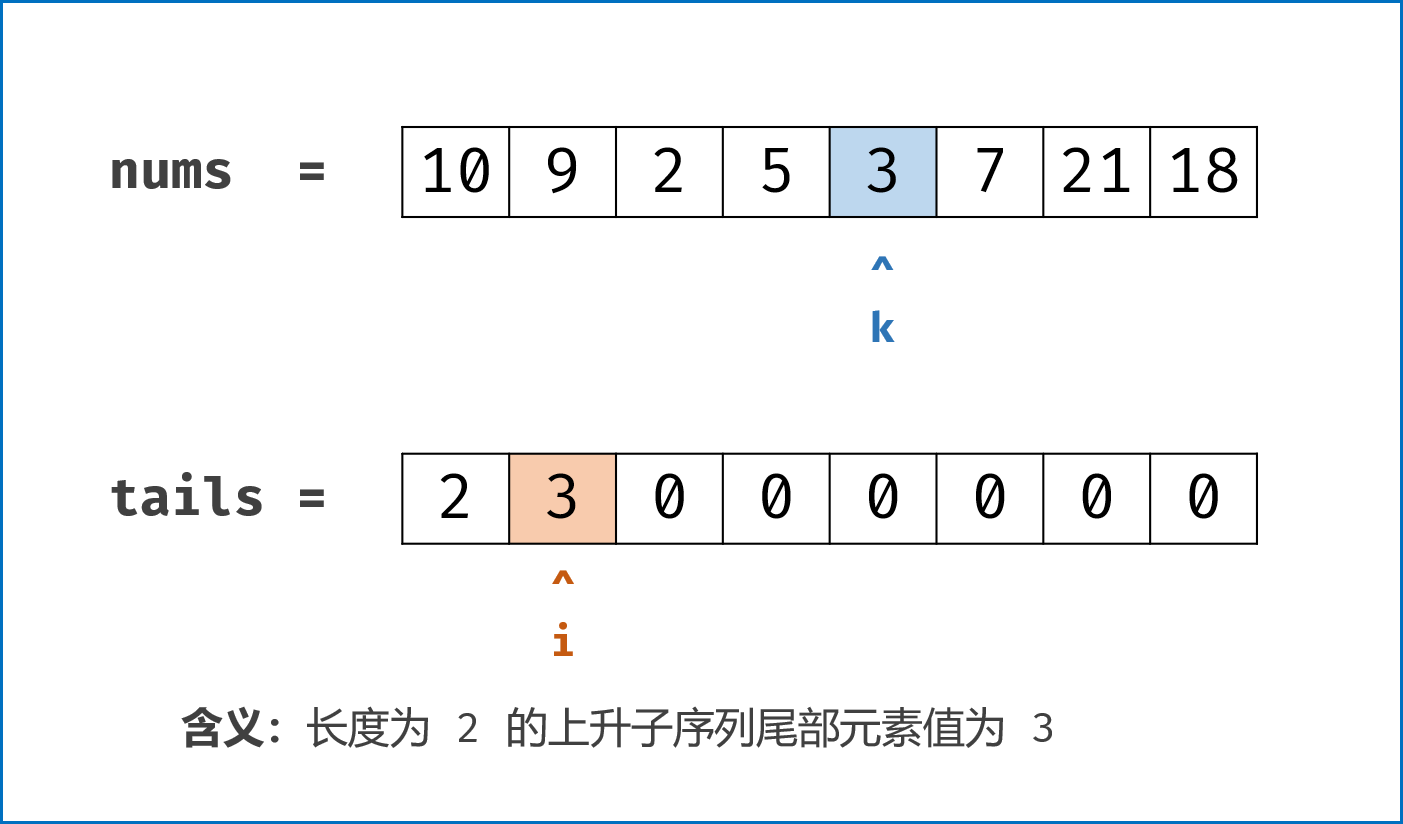
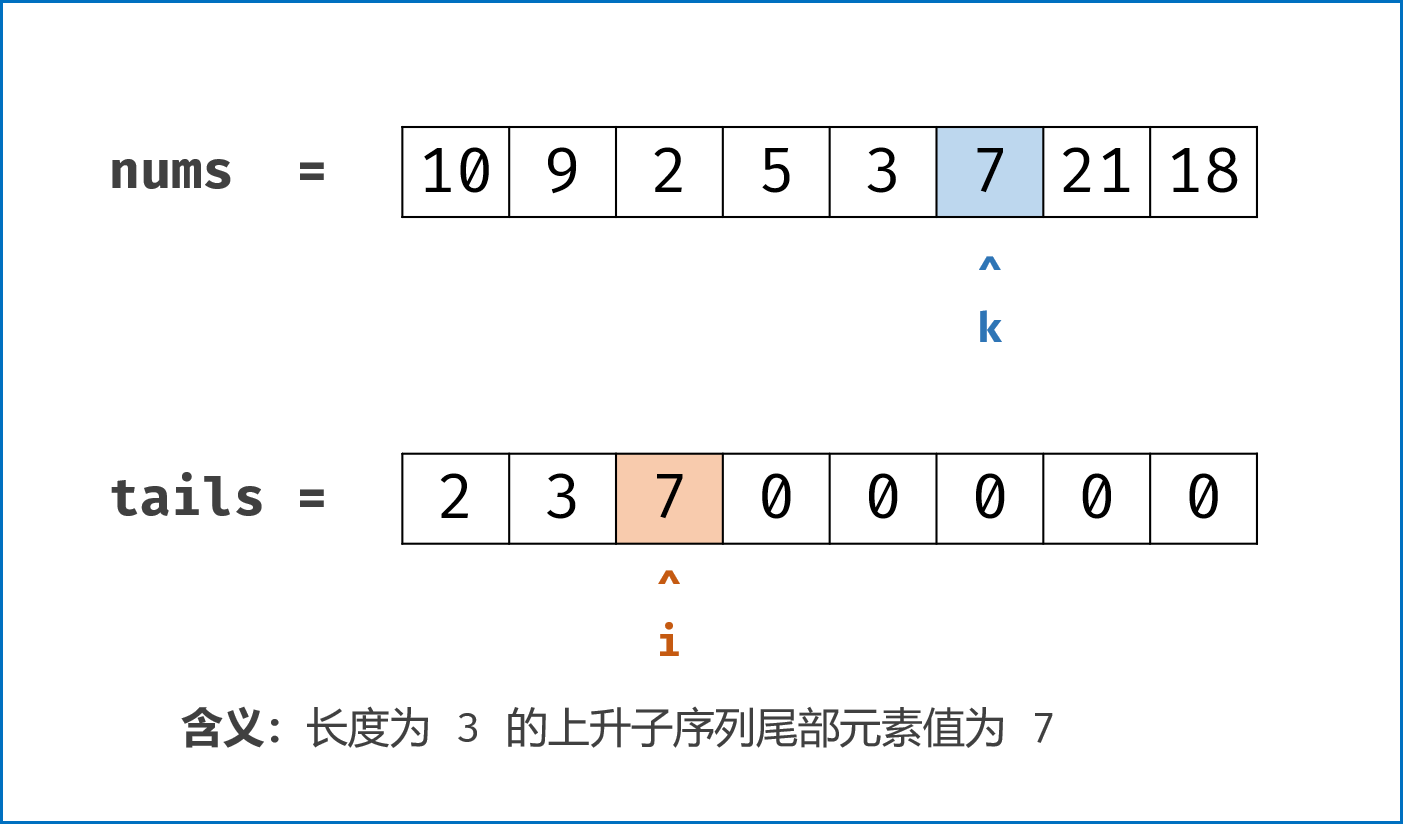
  考虑一个简单的贪心，如果我们要使上升子序列尽可能的长，则我们需要让序列上升得尽可能慢，因此我们希望每次在上升子序列最后加上的那个数尽可能的小。

基于上面的贪心思路，我们维护一个数组 d[i] ，表示长度为 i 的最长上升子序列的末尾元素的最小值，用 len 记录目前最长上升子序列的长度，起始时 len 为 1，d[1]=nums[0]。

d为单调递增的

我们依次遍历数组 nums 中的每个元素，并更新数组 d 和 len 的值。如果 nums[i]>d[len] 则更新 len=len+1，否则在 d[1…len]中找满足 d[i−1]<nums[j]<d[i] 的下标 i，并更新 d[i]=nums[j]。

解释：

• 无序列表最关键的一句在于： 数组 d[i]表示长度为 i 的最长上升子序列的末尾元素的最小值，即在数组 1,2,3,4,5,6中长度为3的上升子序列可以为 1,2,3也可以为 2,3,4等等但是d[3]=3，即子序列末尾元素最小为3。
• 无序列表证明单调性有两个好处：1.可以使用二分法；2.数组d的长度即为最长子序列的长度；

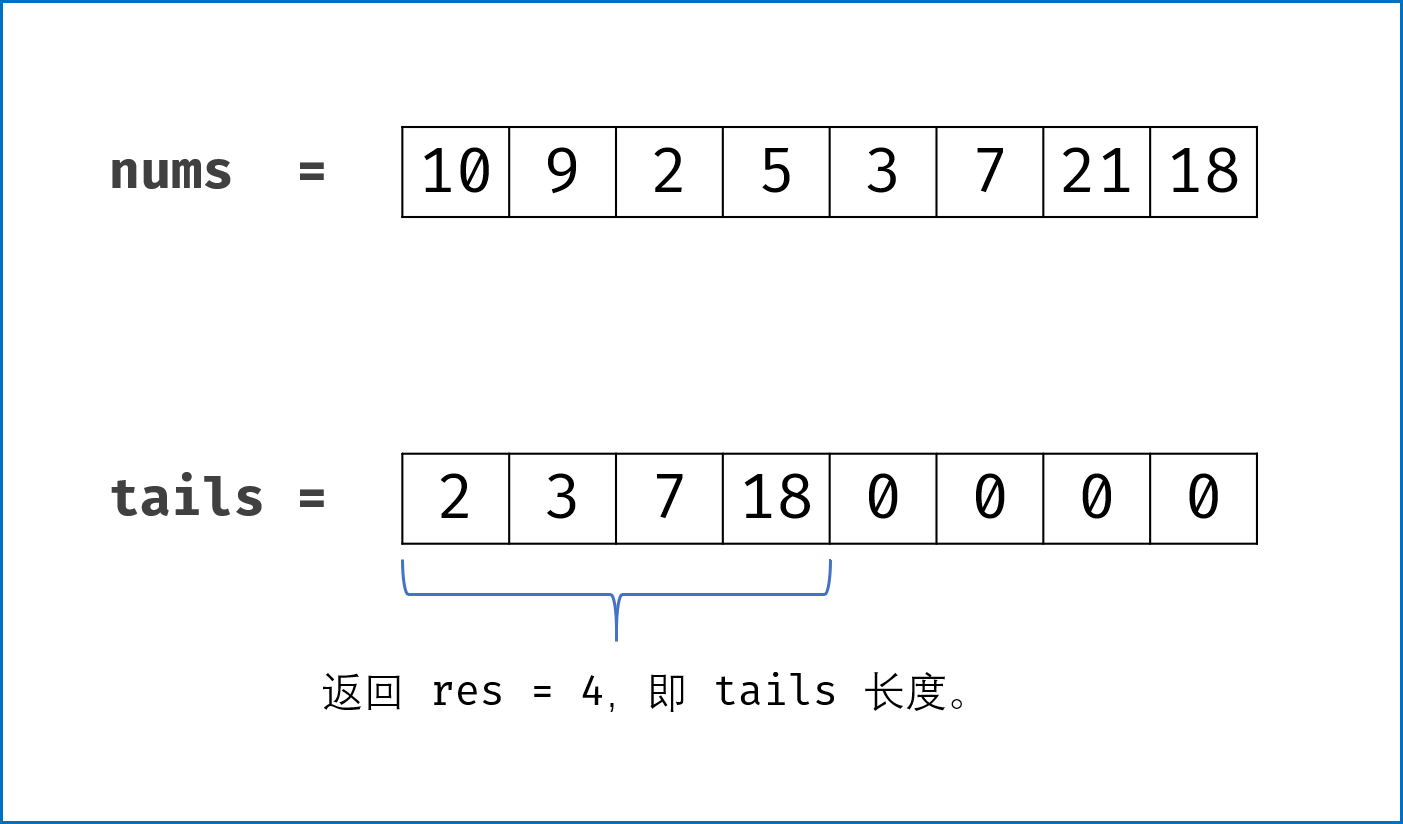
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int len = nums.size();
        if(len<2){
            return len;
        }
        vector<int> d(len+1,0);
        int pos = 1;
        d[pos] = nums[0];
        for(int i=1;i<len;i++){
            if(nums[i]>d[pos]){
                d[++pos] = nums[i];
            }else{
                int l = 1,r = pos;
                //找到比nums[i]大的最小值
                //二分查找模糊查找
                while(l<r){
                    int mid = l + (r-l)/2;
                    if(d[mid]<nums[i]){
                        l = mid+1;
                    }else{
                        r = mid;
                    }
                }
                d[l] = nums[i];
            }
        }
        return pos;
    }
};

class Solution {
    public int lengthOfLIS(int[] nums) {
        if(nums.length == 0){
            return 0;
        }
        int[] tails = new int[nums.length];
        int pos = 0;
        tails[0] = nums[0];
        for(int i = 1; i < nums.length; ++i){
            if(nums[i] > tails[pos]){
                tails[++pos] = nums[i];
            }else{
                // 找到比nums[i]大的最小值
                // 二分模糊查找
                int l = 0, r = pos;
                while(l < r){
                    int mid = l + (r - l)/2;
                    if(tails[mid] < nums[i]){
                        l = mid + 1;
                    }else{
                        r = mid;
                    }
                }
                tails[l] = nums[i];
            }
        }
        return pos + 1;
    }
}

• 时间复杂度 O(nlog n)
• 空间复杂度 O(n)