题目链接

LeetCode

题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

输入： matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出： [[7,4,1],[8,5,2],[9,6,3]]

示例 2：

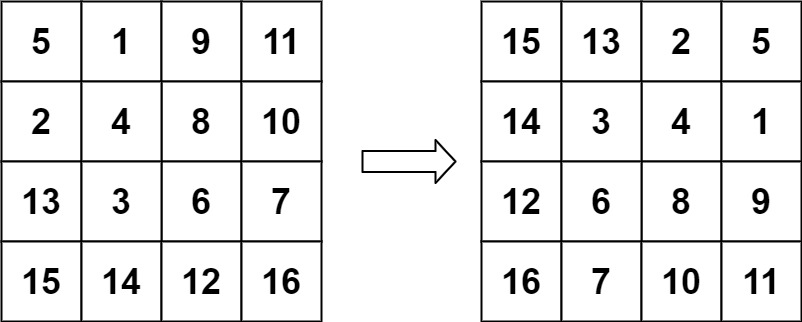
输入： matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出： [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

示例 3：

输入： matrix = [[1]]
输出： [[1]]

示例 4：

输入： matrix = [[1,2],[3,4]]
输出： [[3,1],[4,2]]

提示：

• matrix.length == n
• matrix[i].length == n
• 1 <= n <= 20

• -1000 <= matrix[i][j] <= 1000

  解题思路

  方法一：使用辅助数组

  将每一圈先保存，然后再赋值回去。或者直接用一个一样大的数组保存，然后赋值回来

  class Solution {
  public:
    void rotate(vector<vector<int>>& matrix) {
        int rows = matrix.size();
        if(rows==0)
            return;
        int cols = matrix[0].size();
        int r1=0,c1=0,r2=rows-1,c2=cols-1;
        vector<int> tmp(rows*cols,0);
        int index = 0,s=0;
        while(r1<=r2){
            index = 0;
            for(int i = c1;i<=c2;++i){
                tmp[index++] = matrix[r1][i];
            }
            for(int i = r1+1;i<=r2;++i){
                tmp[index++] = matrix[i][c2];
            }
            if(r1!=r2){
                for(int i = c2-1;i>=c1;--i){
                    tmp[index++] = matrix[r2][i];
                }
            }
            if(c1!=c2){
                for(int i = r2-1;i>r1;--i){
                    tmp[index++] = matrix[i][c1];
                }
            }
            if(index<2)
                break;
            s = 0; 
            for(int i = r1;i<=r2;++i){
                matrix[i][c2] = tmp[s++];
            }
            if(r1!=r2){
                for(int i = c2-1;i>=c1;--i){
                    matrix[r2][i] = tmp[s++];
                }
            }
            if(c1!=c2){
                for(int i = r2-1;i>=r1;--i){
                    matrix[i][c1] = tmp[s++];
                }
            }
            for(int i = c1+1;i<c2;++i){
                matrix[r1][i] = tmp[s++];
            }
            r1++;
            c1++;
            r2--;
            c2--;
        }
    }
  };

• 时间复杂度 O(n^2)

• 空间复杂度 O(n)

  方法二：原地旋转

  将矩阵分成四部分，统一进行旋转
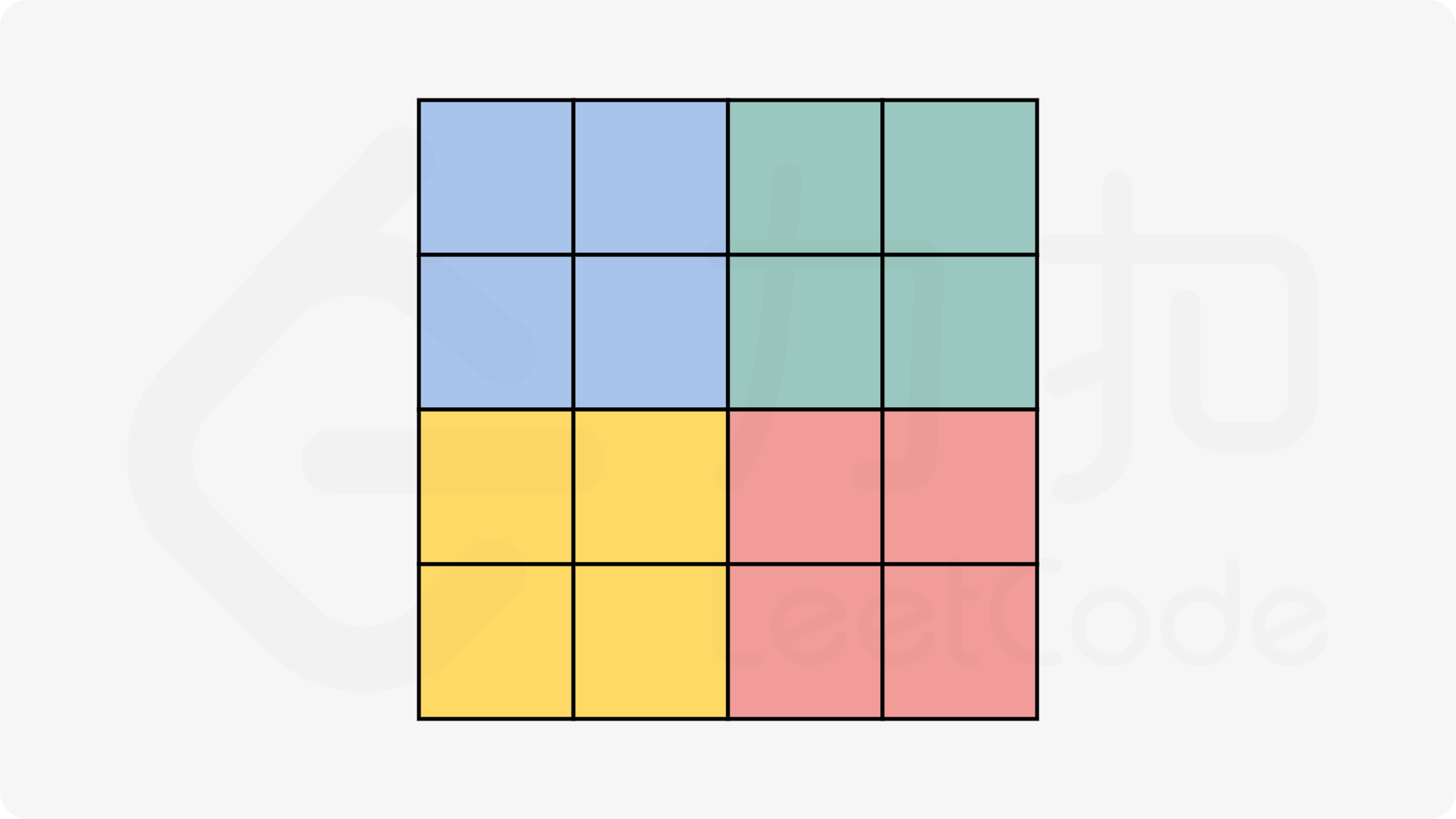
  当 n 为偶数时，我们需要枚举 n^2 / 4 = (n/2)×(n/2) 个位置，可以将该图形分为四块，以 4×4 的矩阵为例：

当 n 为奇数时，由于中心的位置经过旋转后位置不变，我们需要枚举 (n^2-1) / 4 =((n−1)/2)×((n+1)/2) 个位置，需要换一种划分的方式，以 5×5 的矩阵为例：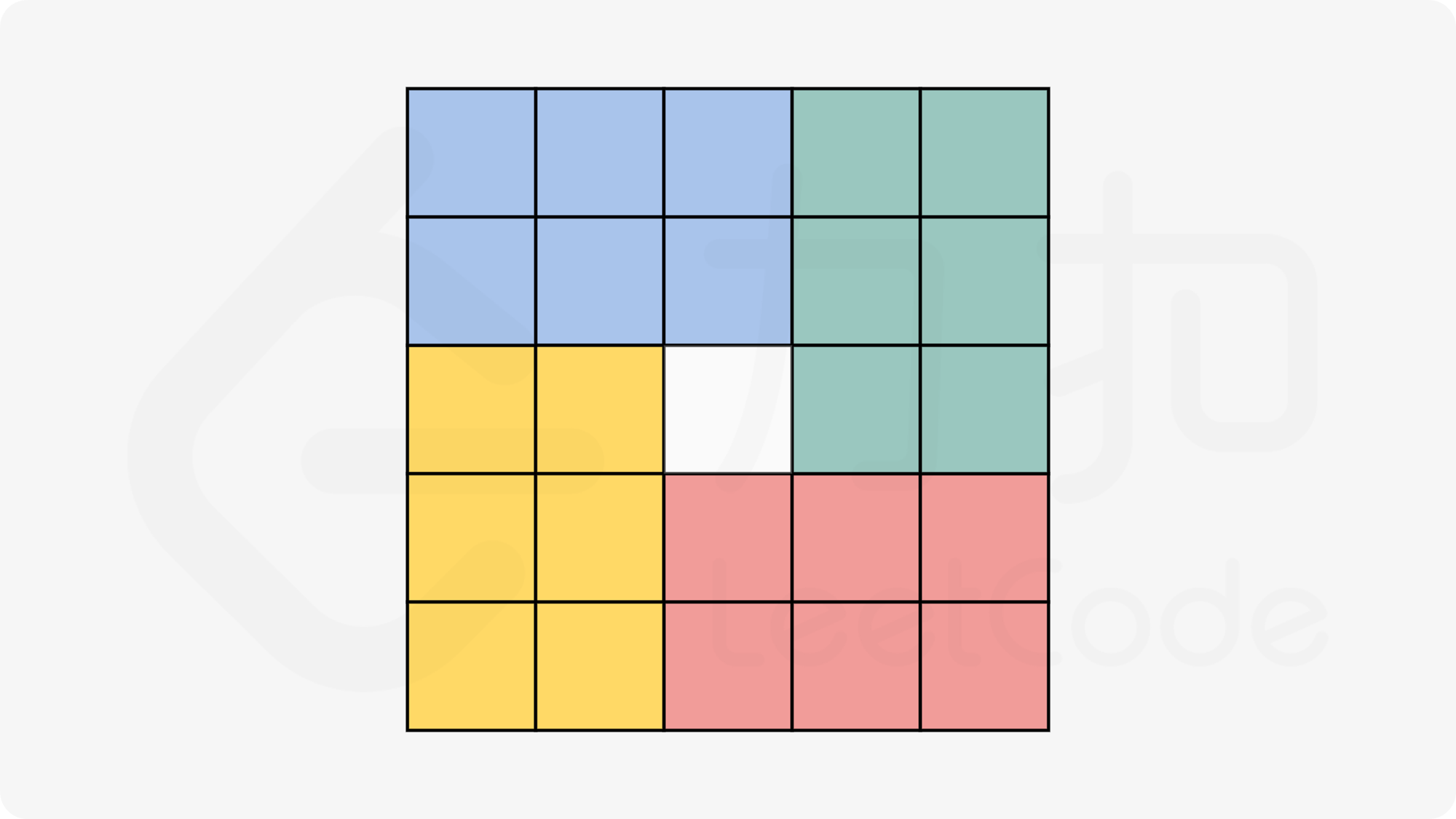

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        if(n<2)
            return;
        for(int i=0;i<n/2;++i){ //i 代表第几行
            for(int j=0;j<(n+1)/2;++j){ //j 代表第几列
                // 当 i 固定时，即遍历第 i 行时
                int tmp = matrix[i][j];
                // matrix[i][j]位置的结果为 i 列从下向上遍历
                matrix[i][j] = matrix[n-1-j][i];
                // matrix[n-1-j][i]位置的结果为 n-1-i 行从右向左遍历
                matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
                // matrix[n-1-i][n-1-j]位置的结果为 n-1-i 列从上向下遍历
                matrix[n-1-i][n-1-j] = matrix[j][n-1-i];
                // matrix[j][n-1-i]位置的结果为 matrix[i][j] 位置的值
                // matrix[j][n-1-i]位置的结果为 i 行从左向右遍历
                matrix[j][n-1-i] = tmp;
            }
        }
    }
};

• 时间复杂度 O(n^2)

• 空间复杂度 O(1)

  方法三：用翻转代替旋转

  先通过水平轴翻转再进行主对角线翻转。
  

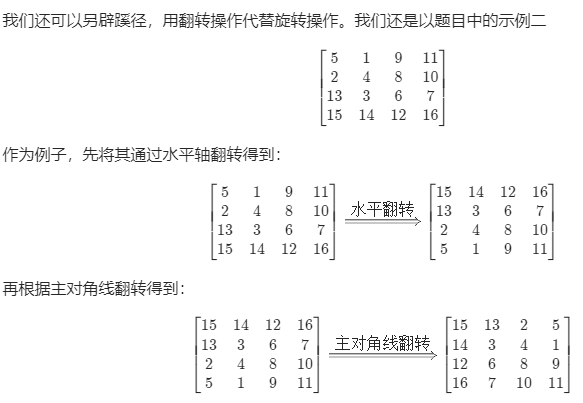
  class Solution {
  public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        // 水平翻转
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                swap(matrix[i][j], matrix[n - i - 1][j]);
            }
        }
        // 主对角线翻转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
  };

  class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // 按主对角线交换
        for(int i=0;i<n;++i){
            for(int j=i+1; j<n;++j){
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = tmp;
            }
        }
        // 按轴对称左右交换 
        for(int i = 0;i<n/2;++i){
            for(int j = 0;j<n;++j){
                int tmp = matrix[j][i];
                matrix[j][i] = matrix[j][n-i-1];
                matrix[j][n-i-1] = tmp;
            }
        }
    }
  }

• 时间复杂度 O(n^2)

• 空间复杂度 O(1)